Сложение и вычитание векторов

Определение

Сложение векторов иосуществляется поправилу треугольника.

Суммой двух векторов иназывают такой третий вектор, начало которого совпадает с началом, а конец - с концомпри условии, что конец вектораи начало векторасовпадают (рис. 1).

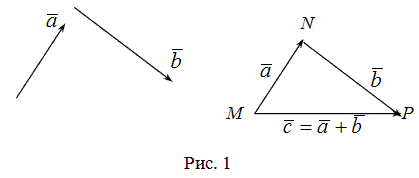
Для сложения векторов применяется также правило параллелограмма.

Определение

Правило параллелограмма - если два неколлинеарных вектора ипривести к общему началу, то векторсовпадает с диагональю параллелограмма, построенного на векторахи(рис. 2). Причем начало векторасовпадает с началом заданных векторов.

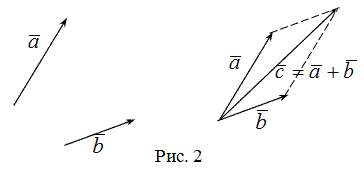
Определение

Вектор называетсяпротивоположным вектором к вектору , если онколлинеарен вектору , равен ему по длине, но направлен в противоположную сторону вектору.

Операция сложения векторов обладает следующими свойствами:

1. - коммутативность

2. - ассоциативность

3. 

4. 

Определение

Разностью векторов иназывается вектортакой, что выполняется условие:(рис. 3).

Умножение вектора на число

Определение

Произведением вектора на число называется вектор, удовлетворяющий условиям:

1. 

2. 

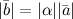
3. , если ,, если.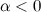

Свойства умножения вектора на число:

1. 

2. 

3. 

4. 

5. 

6. 

Здесь и- произвольные векторы,,- произвольные числа.

Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов: конечномерное вещественное векторное пространство с введённым на нём положительно определённымскалярным произведением, либо метрическое пространство, соответствующее такому векторному пространству. В этой статье за исходное будет взято первое определение.

-мерное евклидово пространство обозначается также часто используется обозначение(если из контекста ясно, что пространство обладает евклидовой структурой).

Для определения евклидова пространства проще всего взять в качестве основного понятие скалярного произведения. Евклидово векторное пространство определяется как конечномерное векторное пространство над полем вещественных чисел, на векторах которого задана вещественнозначная функция обладающая следующими тремя свойствами:

• Билинейность: для любых векторов и для любых вещественных чисели

• Симметричность: для любых векторов

• Положительная определённость: для любого 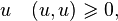причём

Аффинное пространство, соответствующее такому векторному пространству, называется евклидовым аффинным пространством, или просто евклидовым пространством^[1].

Пример евклидова пространства — координатное пространство состоящее из всевозможныхn-ок вещественных чисел скалярное произведение в котором определяется формулой

22. Базис и координаты вектора

Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.

В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:

• Базис Га́меля, в определении которого рассматриваются только конечные линейные комбинации. Базис Гамеля применяется в основном в абстрактной алгебре (в частности в линейной алгебре).

• Базис Ша́удера, в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды. Это определение применяется в основном в функциональном анализе, в частности для гильбертова пространства,

В конечномерных пространствах обе разновидности базиса совпадают.

Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.

где — координаты вектора.

23. Скалярное произведение.

операция над двумя векторами, результатом которой является число [когда рассматриваются векторы, числа часто называют скалярами], не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:

24. Векторное произведение

это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном евклидовом пространстве. Векторное произведение не обладает свойствами коммутативности и ассоциативности (является антикоммутативным) и, в отличие от скалярного произведения векторов, является вектором. Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения. Векторное произведение полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.

• Векторное произведение двух векторов можно вычислить с помощью определителя матрицы

где

25. Смешанное произведение

Сме́шанное произведе́ние векторов —скалярное произведение вектора навекторное произведение векторов и:

.

Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами .смешанное произведение трех векторов можно найти через определитель

26. Плоскость в пространстве

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

Некоторые характеристические свойства плоскости

• Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;

• Две плоскости являются либо параллельными, либо пересекаются по прямой.

• Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.

• Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.

• Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.

Аналогично отрезку и интервалу, плоскость, не включающую крайние точки, можно назвать интервальной плоскостью, или открытой плоскостью.

• Общее уравнение (полное) плоскости

где и— постоянные, причёмиодновременно не равны нулю; ввекторной форме:

где — радиус-вектор точки, векторперпендикулярен к плоскости (нормальный вектор).Направляющие косинусы вектора :

• Уравнение плоскости в отрезках:

где ,,— отрезки, отсекаемые плоскостью на осяхи.

• Уравнение плоскости, проходящей через точку перпендикулярно вектору нормали :

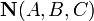в векторной форме:

• Уравнение плоскости, проходящей через три заданные точки ,не лежащие на одной прямой:

27. Нормированное уравнение плоскости

нормальное уравнение плоскости вида задает в прямоугольной системе координатOxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости .

28. Прямая в пространстве

Прямая в пространстве может быть задана как линия пересечения двух плоскостей. Так как точка прямой прнадлежит каждой из плоскостей, то ее координаты обязаны удовлетворять уравнениям обеих плоскостей, то есть удовлетворять системе из двух уравнений.

итак, если уравнения двух непараллельных плоскостей -- и, то прямая, являющаяся их линией пересечения, задается системой уравнений

(11.11)

И наоборот, точки, удовлетворяющие такой системе уравнений, образуют прямую, являющуюся линией пересечения плоскостей, чьи уравнения образуют эту систему.

Уравнения (11.11) называют общими уравнениями прямой в пространстве.

29. Уравнение окружности

Уравнение окружности радиуса с центром вначале координат:

30. Эллипс. Каноническое уравнение. Эксцентриситет, фокальный радиус.

Э́ллипс — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек и(называемыхфокусами) постоянна и больше расстояния между фокусами, то есть

причем

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.

Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.