Доказательство

Самое простое доказательство этой теоремы даётся методами комплексного анализа. Используется тот факт, что функция, аналитическая на всей комплексной плоскости и не имеющая особенностей на бесконечности, есть константа. Посему, функция 1/p, где p — многочлен, должна иметь хоть один полюс на комплексной плоскости, а, соответственно, многочлен имеет хоть один корень.

Следствие

Немедленным следствием из теоремы является то, что любой многочлен степени над полем комплексных чисел имеет в нём ровнокорней, с учётом их кратности.

Доказательство следствия

У многочлена есть корень, значит, потеореме Безу, он представим в виде , где— другой многочлен. Применим теорему ки будем применять её таким же образом до тех пор, пока на местене окажется линейный множитель.

19. Формулы Виета.

Формулы Виета — формулы, выражающие коэффициенты многочлена через его корни.

Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.

Если — корни многочлена

(каждый корень взят соответствующее его кратности число раз), то коэффициенты выражаются в видесимметрических многочленов от корней, а именно:

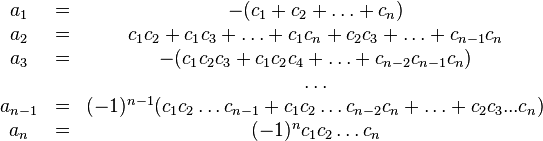
Иначе говоря равно сумме всех возможных произведений изкорней.

Если старший коэффициент многочлена , то для применения формулы Виета необходимо предварительно разделить все коэффициенты на(это не влияет на значение корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему. Из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленен.

Доказательство

Доказательство осуществляется рассмотрением равенства, полученного разложением многочлена по корням, учитывая, что

Приравнивая коэффициенты при одинаковых степенях (теорема единственности), получаем формулы Виета.

20. Рациональная дробь и разложение ее на простейшие дроби.

Простейшие дроби часто называют элементарыми дробями.

Различают следующие виды простейших дробей:

1. 

2. 

3. 

4. 

где A, M, N, a, p, q – числа, а дискриминант знаменателя в дробях 3) и 4) меньше нуля.

Называют их соответственно дробями первого, второго, третьего и четвертого типов.

Вообще отношение многочленов раскладывают на простейшие дроби, если степень многочлена числителя меньше степени многочлена в знаменателе. В противном случае сначала проводят деление многочлена числителя на многочлен знаменателя, а уже затем проводят разложение правильной дробно рациональной функции.

Алгоритм метода неопределенных коэффициентов.

• Во-первых, раскладываем знаменатель на множители.

Здесь все методы хороши – от вынесения за скобки, применения формул сокращенного умножения, до подбора корня и последующего деления столбиком (при знаменателе в виде многочлена с рациональными коэффициентами степени выше второй). Об этом подробнее в разделе теории – разложение многочлена на множители.

В нашем примере все просто – выносим х за скобки.

• Во-вторых, раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами.

Здесь стоит рассмотреть виды выражений, которые могут быть у Вас в знаменателе.

• Если в знаменателе что-то вроде этого , количество линейных множителей роли не играет, (будь их2 или 22), то дробь представится в виде суммы простейших дробей первого типа: a, b, c и d - числа, A, B, C и D - неопределенные коэффициенты.

• Если в знаменателе что-то вроде этого количество множителей роли не играет и не играют роли степени этих множителей (хоть 221ая степень), то дробь представится в виде суммы простейших дробей первого и второго типов:a, b, c - числа, - неопределенные коэффициенты.

Возьмите на заметку: какая степень – столько и слагаемых.

• Если в знаменателе что-то вроде этого 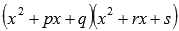количество квадратичных выражений роли не играет, то дробь представится в виде суммы простейших дробей третьего типа:p, q, r и s - числа, P, Q, R и S - неопределенные коэффициенты.

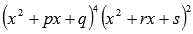• Если в знаменателе что-то вроде этого количество множителей роли не играет и не играют роли степени этих множителей, то дробь представится в виде суммы простейших дробей третьего и четвертого типов:p, q, r и s - числа, - неопределенные коэффициенты.

ОБЫЧНО ВСТРЕЧАЕТСЯ КОМБИНАЦИЯ ЭТИХ ВАРИАНТОВ (как правило, довольно простая).

• Если собрать все в кучу ,то дробь представится в виде суммы простейших дробей всех четырех типов:

Хватит теории, на практике все равно понятнее.

Пришло время вернуться к примеру. Дробь раскладывается в сумму простейших дробей первого и третьего типов с неопределенными коэффициентами A, B и C.

• В-третьих, приводим полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х.

То есть, пришли к равенству:

При x отличных от нуля это равенство сводится к равенству двух многочленов

А два многочлена являются равными тогда и только тогда, когда коэффициенты при одинаковых степенях совпадают.

• В-четвертых, приравниваем коэффициенты при одинаковых степенях х.

При этом получаем систему линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных:

• В-пятых, решаем полученную систему уравнений любым способом (при необходимости смотрите статью решение систем линейных алгебраических уравнений, методы решения, примеры), который нравится Вам, находим неопределенные коэффициенты.

• В-шестых, записываем ответ.

P.S.

Пожалуйста, не ленитесь, проверяйте ответ, приводя к общему знаменателю полученное разложение.

Метод неопределенных коэффициентов является универсальным способом при разложении дроби на простейшие.

Очень удобно использовать метод частных значений, если знаменатель представляет собой произведение линейных множителей, то есть имеет вид схожий с

Рассмотрим на примере, чтобы показать плюсы этого метода.

21. Линейные операции над векторами. Пространство Rn

Линейными операциями над векторами называются операции сложения векторов и умножения вектора на число.