Ранг матрицы

Строки и столбцы матрицы являются элементами соответствующих векторных пространств:

• столбцы матрицы составляют элементы пространства размерности;

• строки матрицы составляют элементы пространства размерности.

Рангом матрицы называют количество линейно независимых столбцов матрицы (столбцовый ранг матрицы) или количество линейно независимых строк матрицы (строчный ранг матрицы). Этому определению эквивалентно определение ранга матрицы как порядка максимального отличного от нуля минора матрицы.

При элементарных преобразованиях ранг матрицы не меняется.

Свойства линейных операций:

Везде далее матрицы ,и- матрицы одного размера.

1. Ассоциативность

2. , где 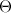-нулевая матрица соответствующего размера.

3. 

4. Коммутативность

5. Дистрибутивность

6. 

7. 

10. Теорема о базисном миноре.

В произвольной матрице каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.

ОПРЕДЕЛЕНИЕ

В матрице минор порядка называетсябазисным, если он не равен нулю, а все миноры порядка и выше равны нулю или не существуют вовсе, т.е. совпадает с меньшим из чисел или.

Следствие. Определитель -го порядка равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.

Теорема о базисном миноре матрицы служит для доказательства таких важных теорем:

Теорема 1. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами).

Теорема 2. (Теорема о ранге матрицы). Для любой матрицы ее ранг равен максимальному количеству ее линейно независимых строк (столбцов).

11. Критерий совместности СЛАУ

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных и бесконечное множество решений, если ранг меньше числа неизвестных.

Для того, чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.

Доказательство (условия совместности системы) Необходимость

Пусть система совместна. Тогда существуют числа такие, что. Следовательно, столбецявляется линейной комбинацией столбцовматрицы. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что.

Достаточность

Пусть . Возьмем в матрицекакой-нибудь базисный минор. Так как, то он же и будет базисным минором и матрицы. Тогда, согласно теореме о базисномминоре, последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы.

Следствия

• Количество главных переменных системы равно рангу системы.

• Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

12. Решение СЛАУ общего вида.

Основная запись СЛАУ. Понятие решения СЛАУ и некоторые определения.В общем случае основная запись системы n линейных алгебраических уравнений с n неизвестными имеет следующий вид:

(2.2.1)

При этом через обозначены неизвестные, подлежащие определению; величиныназываемыекоэффициентами системы, и величины , называемыесвободными членами, предполагаются известными. Каждый коэффициент системы имеет два индекса, первый из которыхуказывает номер уравнения, а второйномер неизвестного, при котором стоит этот коэффициент.

Система называется однородной, если все ее свободные члены равны нулю.

Если хотя бы один из свободных членов отличен от нуля, то система называетсянеоднородной.

Решением системы называется такая совокупность чисел, которая при подстановке в систему на место неизвестныхобращает все уравнения этой системы в тождества.

Система уравнений вида называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее не существует ни одного решения.

Совместная система вида называется определенной, если она имеет единственное решение.

Совместная система вида называется неопределенной, если у нее существуют по крайней мере два различных решения.

Краткая запись СЛАУ:

. (2.2.2)

Матричная формулировка СЛАУ:

, (2.2.3)

где

; (2.2.4)

–матрица коэффициентов системы; – вектор неизвестных;– вектор свободных членов.

Представление с помощью расширенной матрицы.В действительности, система уравнений полностью определяется элементами матрицы и вектора правой части. Обозначения неизвестных имеют чисто символический смысл. При различных допустимых преобразованиях системы также меняются только значения элементов матрицы и правой части. Поэтому вполне достаточным представлением системы уравнений является, так называемая, расширенная матрица (она получается из матрицы коэффициентов системы путем добавления к этой матрице столбца свободных членов):

(2.2.5)

где .

Прямые методами решения СЛАУ называются методы, которые позволяют получить теоретически точное (с учетом ограниченности разрядной сетки ЭВМ) решение за конечное число операций. Прямым методом является, в частности, метод Гаусса,

13. Решение однородной СЛАУ.

Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, x1=0, x2=0, x3=0 и x4=0 в записанную выше систему. Получим два верных равенства:

{2⋅0−3⋅0−0−0=0;−4⋅0+5⋅0+3⋅0=0.

Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой).

С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен r, то такая СЛАУ имеет n−r линейно независимых решений: φ1, φ2,..., φn−r.

Любая совокупность n−r линейно независимых решений однородной СЛАУ называется фундаментальной системой (или совокупностью) решений данной СЛАУ.

Часто вместо словосочетания "фундаментальная система решений" используют аббревиатуру "ФСР". Если решения φ1, φ2,..., φn−r образуют ФСР, и X – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде:

X=C1⋅φ1+C2⋅φ2+…+Cn−r⋅φn−r,

где C1, C2,..., Cn−r – произвольные постоянные.

14. Метод Гаусса

классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы

15. Структура общего решения неоднородной СЛАУ.

Вспомним одно из свойств решений линейной неоднородной системы:

Если и— два решения системы, то вектор— решение приведенной однороднойсистемы .

Поскольку выражение

задает все решения однородной системы, то для любых двух решений инеоднородной системы справедливо

и, следовательно, выражение

определяет любое решение неоднородной системы.

Таким образом доказана теорема о структуре общего решения линейной неоднородной системы.

Теорема. Если ранг r матрицы неоднородной системы линейных уравнений мерньше числа неизвестных n, то общее решение системы можно записать в виде

где — произвольные константы, а— фундаментальная система решений однородной системы,— некоторое известное (частное) решение неоднородной системы.

16. Многочлены. Операции над многочленами.

Одночленом степени (здесь) называется следующее выражение

где -- коэффициент,- переменная.

Многочленом - ой степени (здесь ) с вещественными коэффициентаминазывается следующее выражение:

здесь - переменная. Можно сказать, что многочлен - это линейная комбинация одночленнов разных степеней.

Операции над многочленами:

Пусть два многочлена степениисоответственно, т.е.

предположим, что .

1. Сумма и разность многочленов: .

Суммой и разностью многочленов иназывается следующий многочлен:

Степень полученного многочлена не превосходит максимальной степени многочленови.

2. Умножение на одночлен: .

Умножим одночлен на многочлен:

т.е. каждый член многочлена умножается на одночлен. Здесь применяем правило работы со степенями.

3. Умножение многочленов: .

Умножим многочлен на:

В итоге свели операцию умножения многочленов к умножению одночлена на многочлен. Заметим, что при умножении многочленов степени иполучается многочлен степени. При умножении многочленов необходимо каждый член одного многочлена умножить на каждый член другого многочлена.

4. Деление многочленов: .

Разделим многочлен на, т.е. представим выражениев следующем виде:

где -- частное от деления,-- делимое,-- делитель,-- остаток.

При делении многочлена на многочлен, где, нужно найти многочленыитакие, чтобы выполнялось равенство

Существует много способов поиска таких многочленов. В основном используются школьные способы, а именно, деление "уголком" ("столбиком") и метод неопределенных коэффициентов (будут рассмотрены ниже).

17. Теорема Безу. Схема Горнера.

Теорема Безу утверждает, что остаток от деления многочлена на многочленравен.Предполагается, что коэффициенты многочлена содержатся в некоторомкоммутативном кольце с единицей (например, в поле вещественных или комплексных чисел).

Доказательство

Поделим с остатком многочлен на многочлен:

Так как , то— многочлен степени не выше 0. Подставляя, поскольку, имеем.

Следствия

• Число являетсякорнем многочлена тогда и только тогда, когдаделится без остатка на двучлен(отсюда, в частности, следует, что множество корней многочленатождественно множеству корней соответствующего уравнения).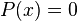

• Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).

• Пусть — целый кореньприведённого многочлена с целыми коэффициентами. Тогда для любого целогочислоделится на.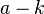

Схе́ма Го́рнера (или правило Горнера, метод Горнера) — алгоритм вычисления значения многочлена, записанного в виде суммы мономов (одночленов), при заданном значении переменной. Метод Горнера позволяет найти корни многочлена^[1], а также вычислить производные полинома в заданной точке. Схема Горнера также является простым алгоритмом для деления многочлена на бином вида . Метод назван в честьУильяма Джорджа Горнера. Пример №1

Разделить 5x4+5x3+x2−11 на x−1, используя схему Горнера.

Решение

Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 5x4+5x3+x2−11, расположенные по убыванию степеней переменной x. Заметьте, что данный многочлен не содержит x в первой степени, т.е. коэффициент перед x в первой степени равен 0. Так как мы делим на x−1, то во второй строке запишем единицу:

Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число 5, просто перенеся его из соответствующей ячейки первой строки:

Следующую ячейку заполним по такому принципу: 1⋅5+5=10:

Аналогично заполним и четвертую ячейку второй строки: 1⋅10+1=11:

Для пятой ячейки получим: 1⋅11+0=11:

И, наконец, для последней, шестой ячейки, имеем: 1⋅11+(−11)=0:

Задача решена, осталось только записать ответ:

Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления 5x4+5x3+x2−11 на x−1. Естественно, что так как степень исходного многочлена 5x4+5x3+x2−11 равнялась четырём, то степень полученного многочлена 5x3+10x2+11x+11 на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остачу от деления многочлена 5x4+5x3+x2−11 на x−1. В нашем случае остача равна нулю, т.е. многочлены делятся нацело. Этот результат ещё можно охарактеризовать так: значение многочлена 5x4+5x3+x2−11 при x=1 равно нулю.

Можно сформулировать вывод и в такой форме: так как значение многочлена 5x4+5x3+x2−11 при x=1 равно нулю, то единица является корнем многочлена 5x4+5x3+x2−11.

18. Основная теорема алгебры.

Основна́я теоре́ма а́лгебры утверждает, что поле комплексных чисел алгебраически замкнуто, то есть

Всякий отличный от константы многочлен (от одной переменной) с комплексными коэффициентами имеет, по крайней мере, один корень на поле комплексных чисел.

Данное утверждение справедливо и для многочленов с вещественными коэффициентами, так как всякое вещественное число является комплексным с нулевой мнимой частью.

Не существует строго алгебраического доказательства теоремы — все имеющиеся привлекают неалгебраические концепции, вроде полноты множества вещественных чисел или топологии комплексной плоскости. К тому же, теорема не является "основной" в современной алгебре — она получила это название во времена, когда основным направлением алгебры был поиск решений алгебраических уравнений с вещественными и комплексными коэффициентами.