
- •26. Космические скорости.
- •27. Движение в неинерциальных системах. Принцип эквивалентности.
- •Уравнение движения тела переменной массы
- •30. Закон сохранения момента импульса. Момент импульса
- •31. Механика твердого тела: вращение тела вокруг неподвижной оси.
- •33. Кинетическая энергия вращающихся тел.
- •34. Моменты инерции. Теорема Штейнера.
- •36. Сокращение длины и замедление времени в сто.
- •37. Закон сложения скоростей в сто.
- •38. Масса и энергия в сто.
- •39. Основной закон динамики, сила в сто.
- •40. Связь энергии и импульса в сто.
40. Связь энергии и импульса в сто.
Если частица
с массой m движется со скоростью  ,
то её энергия и импульс имеют следующую
зависимость от скорости:
,
то её энергия и импульс имеют следующую
зависимость от скорости:

Эти соотношения
обобщают классические выражения для
энергии и импульса, получающиеся в
результате разложения в ряд по 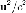 :
:
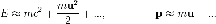
При нулевой
скорости, энергия частицы называется
энергией покоя:  .
В современной физической литературе,
принято, чтоm —
масса частицы не
зависит от скорости, являясь инвариантом
относительно преобразований Лоренца,
и является величиной неаддитивной.
Понятие «релятивистской массы», зависящей
от скорости
.
В современной физической литературе,
принято, чтоm —
масса частицы не
зависит от скорости, являясь инвариантом
относительно преобразований Лоренца,
и является величиной неаддитивной.
Понятие «релятивистской массы», зависящей
от скорости  не
используется[25] ,
хотя оно и встречается в ранних работах
по теории относительности. Историческая
причина введения этого понятия была
связана с попытками сохранить для
релятивистского импульса классическую
форму:
не
используется[25] ,
хотя оно и встречается в ранних работах
по теории относительности. Историческая
причина введения этого понятия была
связана с попытками сохранить для
релятивистского импульса классическую
форму: 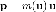 .
.
При приближении скорости тела к скорости света, его энергия и импульс стремятся к бесконечности. Это одна из причин, по которой «обычные» объекты неспособны двигаться быстрее скорости света. Для частицы с ненулевой массой даже достижение скорости света потребует затраты бесконечной энергии. Заметные отклонения от классических выражений для энергии и импульса происходят при скоростях близких к скорости света. Если скорости относительно невелики, то отклонения от классической динамики незначительны. Например, при скорости u=c/4, относительная разница релятивистского и классического импульса составляет всего 3 %.
Между релятивистской энергией и импульсом существуют следующие связи:
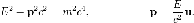
Эти формулы
остаются справедливыми и для объектов,
движущихся со скоростью света. В этом
случае их масса должна быть равна нулю  .
.
