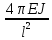25) Плоский и пространственный косой изгиб. Силовая плоскость и силовая линия. Нулевая линия. Определение напряжений и перемещений в балках при косом изгибе.

Пространственный косой изгиб возникает при действии нагрузок, расположенных в разных плоскостях.

Плоский косой изгиб - частный случай косого изгиба, при котором равнодействующие внешних сил в каждом сечении балки лежат в одной плоскости, называемой силовой, а пары - в плоскостях, ей параллельных. В общем случае плоского косого изгиба упругая линия - плоская кривая, плоскость которой не параллельная силовой плоскости. Линия пересечения силовой плоскости с поперечным сечением называется силовой линией.

При косом изгибе нулевая линия - прямая, проходящая через начало координат.

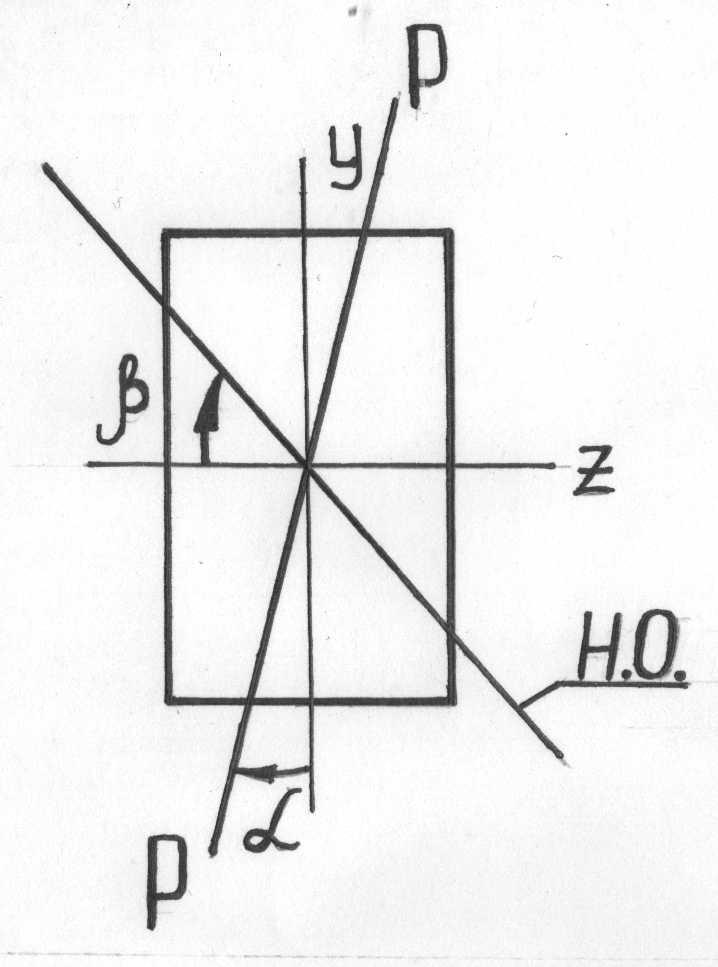
Определение напряжений при косом изгибе

Используя принцип независимости действия сил (принцип суперпозиции) найдем напряжения при косом изгибе. Рассмотрим точку A с координатами (y, z) в сечении изгибаемой балки и определим в ней напряжения от каждого из внутренних усилий, возникающих при косом изгибе:

нормальные напряжения от изгибающего момента M_z

нормальные напряжения от изгибающего момента M_y

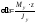
касательные напряжения от поперечной силы Q_y

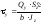
касательные напряжения от поперечной силы Q_z

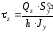
Полные напряжения и при косом изгибе найдем путем геометрического суммирования составляющих:

а) касательных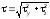

б) нормальных

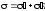
Последнюю формулу удобно представить в виде

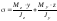
или

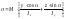
где – угол наклона силовой плоскости P при косом изгибе (а при сложном изгибе – угол наклона плоскости действия полного изгибающего момента M в данном сечении).

Определение деформаций при косом изгибе

Главными центральными осями инерции являются оси x и y.

При теоретическом определении прогибов, действующие на балку нагрузки целесообразно разложить на составляющие в главных плоскостях инерции. Перемещения центра тяжести поперечного сечения бруса от составляющих F_x и F_y нагрузок, расположенных в главных плоскостях инерции xoy и xoz будут соответственно равны fy и fz. Для консольной балки, нагруженной на свободном конце силой F, компоненты полного перемещения свободного конца определяются по формулам:

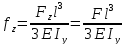
α – угол между силовой плоскостью и главной плоскостью инерции xoy.

Тогда полное перемещение f и угол β между плоскостью изгиба и направлением одной из главных центральных осей инерции будут определяться так:

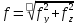
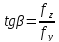
26) Косой изгиб. Определение напряжений и прогибов при косом изгибе. Определение напряжений при косом изгибе

Используя принцип независимости действия сил (принцип суперпозиции) найдем напряжения при косом изгибе. Рассмотрим точку A с координатами (y, z) в сечении изгибаемой балки и определим в ней напряжения от каждого из внутренних усилий, возникающих при косом изгибе:

нормальные напряжения от изгибающего момента M_z

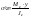
нормальные напряжения от изгибающего момента M_y

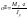
касательные напряжения от поперечной силы Q_y

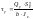
касательные напряжения от поперечной силы Q_z

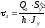
Полные напряжения и при косом изгибе найдем путем геометрического суммирования составляющих:

а) касательных

б) нормальных

Последнюю формулу удобно представить в виде

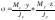
или

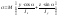
где – угол наклона силовой плоскости P при косом изгибе (а при сложном изгибе – угол наклона плоскости действия полного изгибающего момента M в данном сечении).

Нейтральная ось - геометрическое место точек, в которых продольные нормальные напряжения равны нулю. Прогибы  На практике очень часто встречаются случаи совместной работы стержня на изгиб и на растяжение или сжатие. Подобного рода деформация может вызываться или совместным действием на балку продольных и поперечных сил, или только одними продольными силами.

Первый случай изображен на Рис.1. На балку АВ действуют равномерно распределенная нагрузка q и продольные сжимающие силы Р.

Рис.1 Совместное действие изгиба и сжатия.

 Предположим, что прогибами балки по сравнению с размерами поперечного сечения можно пренебречь; тогда с достаточной для практики степенью точности можно считать, что и после деформации силы Р будут вызывать лишь осевое сжатие балки. Применяя способ сложения действия сил, мы можем найти нормальное напряжение в любой точке каждого поперечного сечения балки как алгебраическую сумму напряжений,вызванных силами Р и нагрузкой q.

Сжимающие напряжения σ_Pот сил Р равномерно распределены по площади F поперечного сечения и одинаковы для всех сечений:

нормальные напряжения от изгиба в вертикальной плоскости в сечении с абсциссой х, которая отсчитана, скажем, от левого конца балки, выражаются формулой

Таким образом, полное напряжение в точке с координатой z (считая от нейтральной оси) для этого сечения равно

27) при внецентренном растяжении (сжатии) в по­перечном сечении бруса возникает нормальная сила N_z= P и изгибающие моменты M_x и M_y . Нормальное напряжение  определяется следующим выражением:

Используя выражения для квадратов радиусов инерции сечения: можно преобразовать к следующему виду: Уравнение нейтральной линии получим, приравнивая нулю выражение для нормальных напряжений : Из можно легко определить отрезки, которые отсекает нейтральная линия на координатных осях. Если приравнять x = 0, то получим:

где a_y   координата точки пересечения нейтральной линии и оси y. Решая это уравнение, получим: Аналогичным образом можно определить координату пересечения нейтральной линии и оси x:

Можно решить и обратную задачу  определить координаты приложения силы Р при заданных отрезках а_x и а_y . Опуская простейшие выкладки, приведем окончательные выражения: Наибольшее напряжения, как и при косом изгибе, имеют место в точке наиболее удаленной от нейтральной линии. При внецентренном растяжении (сжатии) в отличие от косого изгиба нейтральная линия не проходит через центр тяжести сечения.

Рис 5.32

         по мере того, как точка приложения силы приближается к центру тяжести сечения, нейтральная линия удаляется от него. ядром сечения называется область вокруг центра тяжести поперечного сечения, которая обладает следующим свойством: если внецентренно приложенная нагрузка расположена в области ядра, то нормальные напряжения во всех точках поперечного сечения имеют один знак. Для построения ядра сечения необходимо провести нулевые линии, соответствующие их предельному состоянию (это будут касательные к нашему сечению), для каждой из этих линий найти соответствующую ей точку приложения силы и, соединяя полученные точки, получить контур, который и будет являться ядром сечения. Чтобы облегчить построение ядра сечения используют свойство нейтральной линии: при повороте нейтральной линии вокруг некоторой фиксированной точки контура сечения точка приложения силы перемещается вдоль некоторой прямой.

28)

29)

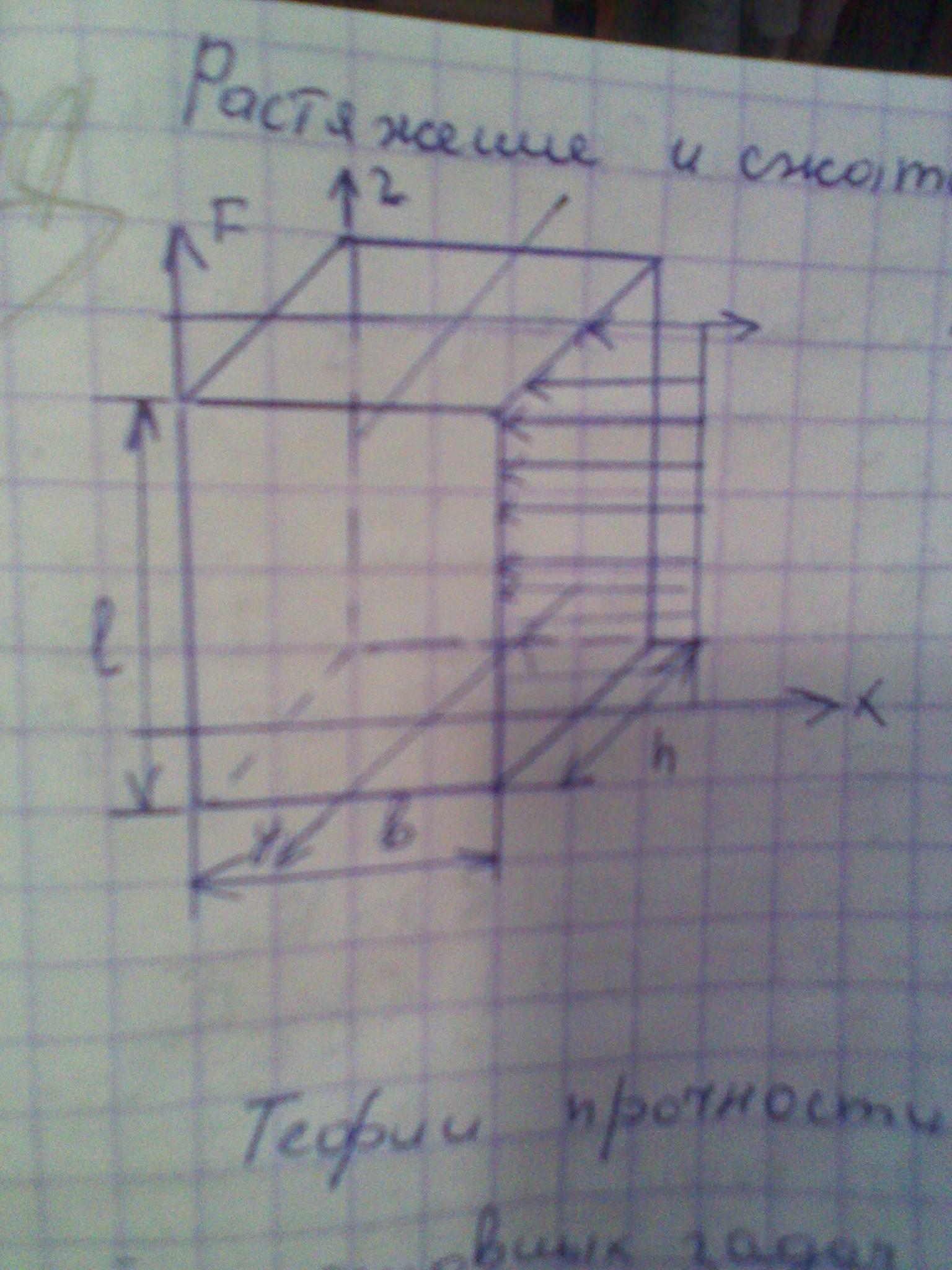
30) Сдвиг- это вид деформации, при котором одна часть стержня смещается относительно другой. Деформация сдвига будет происходить, если к стержню приложить две равные по модулю противоположно направленные силы, перпендикулярные к его оси z.

Касательные напряжения при сдвиге определяются из выражения:

τ =

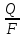
где Q – перерезывающая сила в поперечном сечении

F – площадь среза

Срезу предшествует деформация – искажение прямого угла между двумя взаимно-перпендикулярными линиями. При этом на гранях выделенного элемента (рис. 2.13, в) возникают касательные напряжения. Величина α смещения граней называется абсолютным сдвигом. Значение абсолютного сдвига зависит от расстояния h между плоскостями действия сил F. Более полно деформацию сдвига характеризует угол γ, на который изменяются прямые углы элемента – относительный сдвиг:

tg γ = α/h ≈ γ

31) Критическая нагрузка (Р_к) – такая нагрузка, при которой мы будем иметь состояние равновесия, когда исключается вероятность сохранения стержнем заданной ему прямолинейной формы.

Формула Эйлера для критической силы:

Рк =

Где J – минимальный момент инерции

Данная формула Эйлера справедлива лишь для стержня с шарнирно-опертыми концами и изменится при изменении условий закрепления концов стержня.

1. Критическая сила для стержня длиной l с одним защемленным, а другим свободным концами будет:

Рк =

2. Критическая сила для стержня с защемленными концами, длиной l, равна:

Рк =