
- •Матрицы. Операции над матрицами.
- •Определители 2, 3-го порядков. Свойства определителей.
- •К любой строке( столбцу) матрицы прибавить другую строку (столбец), умноженную на любое число
- •Умнож. Всех элементов строк (столбцов) на число (кроме 0)
- •Системы линейных уравнений. Матричный метод.
- •Системы линейных уравнений. Правило Крамера.
- •Решение произвольных систем линейных уравнений.
- •Линейные пространства.
- •Линейно-независимые векторы. Базис.
- •Метод Гаусса.
- •Метод Жордано-Гаусса
- •14.Скалярное произведение векторов. Ортонормированные базисы.
- •Векторное произведение векторов.
- •Смешанное произведение векторов.
- •Уравн. Плоскости по точке и вектору нормали. Общее уравн. Плоскости.
- •Нормальное уравнение плоскости. Уравнение прямой по двум точкам.
- •Каноническое уравнение прямой линии в пространстве. Уравнение прямой по двум точкам.
- •Взаимное расположение 2-ух прямых в пространстве.
- •Нормальное уравнение прямой на плоскости. Расстояние от точки до прямой.
- •Угловой коэффициент прямой линии на плоскости. Взаимное расположение прямых.
- •Эллипс.
- •Гипербола.
- •Парабола.
- •Поверхности 2-го порядка (эллипсоид, гиперболоиды).
- •Поверхности 2-го порядка (конус, параболоиды).
- •Поверхности 2-го порядка (цилиндры).
- •Предел последовательности. Необходимый признак сходимости.
- •Монотонные последовательности. Достаточный признак сходимости.
-
Матрицы. Операции над матрицами.
Матрицы
размерности (m n)—прямоуг.
табл. Из m
n)—прямоуг.
табл. Из m n
чисел, запис. В виде A=
n
чисел, запис. В виде A=
 (m-
число строк, n-
число столбцов)
(m-
число строк, n-
число столбцов)
Операции над матрицами:
1
0 0
0
1 0 0
0 1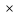 (А+В)=
α A+
α B;
(А+В)=
α A+
α B;
(α β) А= α (β А); (α+β) А= α А+ β А; 1 А=А.
А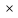 В
В В
В А;
(А
А;
(А В)
В) С=А
С=А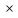 (В
(В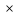 С);
А
С);
А Е=Е
Е=Е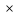 А=А(для
квадратных матриц , Е= )
А=А(для
квадратных матриц , Е= )
Умножение матриц (если число строк одной матрицы = чисту столбцов другой):

-
Определители 2, 3-го порядков. Свойства определителей.

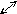 det
A=
det
A=
 =
а11
=
а11
 а22
– а12
а22
– а12
 а21
а21
det
A=

Свойства определителей:
-
Менять местами строки (столбцы)—меняется знак определителя
-
Если к любой строке( столбцу) матрицы прибавить другую строку (столбец), умноженную на любое число, определитель не изменится
-
Если любую строку (столбец) матрицы умнож. на любое число, то определитель тоже умножится на это число.
-
det E= 1
-
det(А
 В)=
det
А
В)=
det
А det
B
(для квадратных матриц)
det
B
(для квадратных матриц)
-
Определители n- го порядка.
-
Разложение по элементам строки или столбца:
*
* *
*

(Aij—алгебр.
дополнение: (-1)i+j det
det
(вычерк. строке и столбец, определитель того,
что осталось))
4 7 9
0 5 4
-
0 0 3
Приведение к треугольному виду: (ниже диагонали—0)
-
Обратная матрица.
Чтобы
обратная матрица существовала, надо,
чтобы det 0
0
А-1 А= А А-1=Е
1 А11
А21 … Аn1 A12
A22 … An2 An1
An2 … Ann
*
* *
*
det
A
(вычерк. строке и столбец, определитель того, что осталось))
-
Элементарные преобразования матриц.
-
перестановка местами строк (столбцов)
-
умнож. всех элементов строк (столбцов) на число (кроме 0)
-
к любой строке( столбцу) матрицы прибавить другую строку (столбец), умноженную на любое число
-
Ранг матрицы.
Ранг матрицы— наибольший порядок минора, отлич. от 0. Минор (МJi) —det матрицы, составленной из элементов, стоящих на пересечении строк и столбцов этой матрицы. (j—столбцы, i—строки).
2 1 5 -1 2 0 -4 5 -3 2 1 3 -1 2 1 -4 5 2
2 1 5 3
-1 2 0 1 -4 5 -3 2
А= М11=2 ; М1122=5; М112233= =0; М112243= = 5 rA= 3
Свойства ранга матриц:
-
притранспонировании (замена строк на столбцы) ранг не меняется
-
перестановка строк (столбцов) местами
-
К любой строке( столбцу) матрицы прибавить другую строку (столбец), умноженную на любое число
-
Умнож. Всех элементов строк (столбцов) на число (кроме 0)
-
вычеркивание нулевого ряда
Если привести матрицу к трапециевидному виду, то ее ранг будет равен числу ненулевых строк.
-
Системы линейных уравнений. Матричный метод.
 а11
х1
+а12
х2+…
+а1n
хn
= b1
а11
х1
+а12
х2+…
+а1n
хn
= b1
a21 x1 +a22 x2 +…+a2n xn = b2 (из коэфициентов перед х составляем матрицу)
am1 x1 +am2 x2 +… +amn xn =bm










а11 а12 а1n х1 b1 х1 b1
a21 a22 a2n х2 = b2 : х2 = А-1 b2 -- матричный метод
am1 am2 amn хn bm хn bm
