Дифференциальные уравнения 2-го порядка
ОДУ 2-го порядка имеет вид:
или
.
Задача
Коши для этого уравнения: найти такое
решение, которое удовлетворяет начальным
условиям
,
.
Решение ду 2-го порядка методом Рунге-Кутта
С
помощью замены переменных
вместо одного ДУ 2-го порядка
получим систему двух ДУ 1-го порядка:
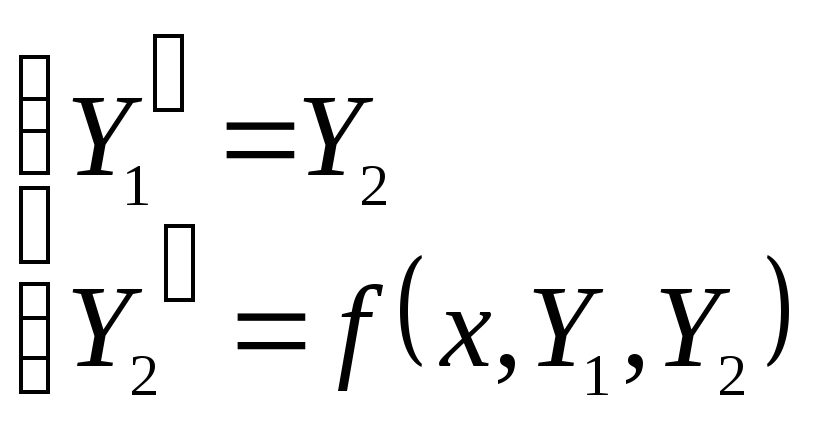
с вектором начальных условий
.
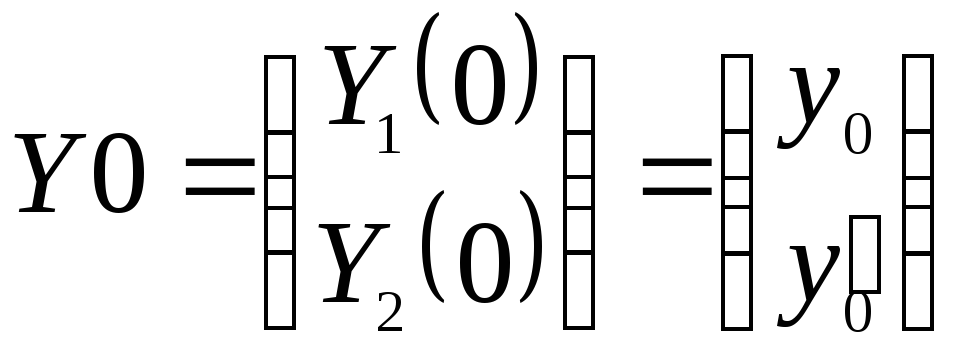Дальше
применяем метод Рунге-Кутта с помощью
встроенной функции
,
где
.
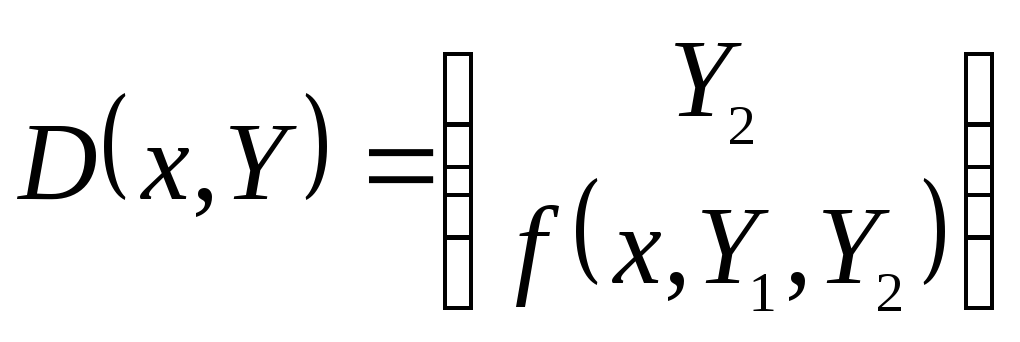Задача
3.
Решите задачу Коши методом Рунге-Кутта
и постройте график приближенного решения
ДУ
,
,
,
по 60 точкам отрезка
.
С помощью замены
,
вместо заданного ДУ получим систему ДУ
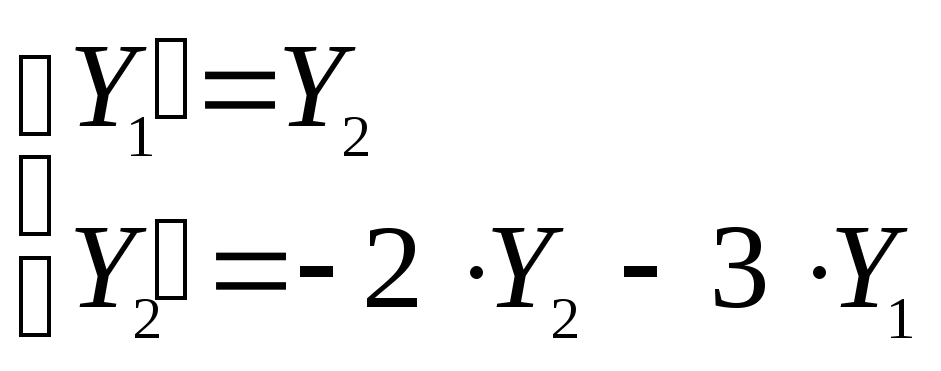
с
вектором начальных условий
.
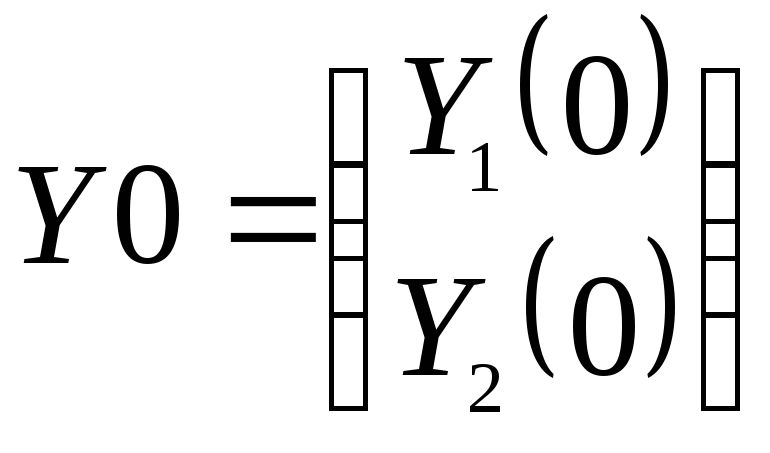Решение:
1)
2)
3)
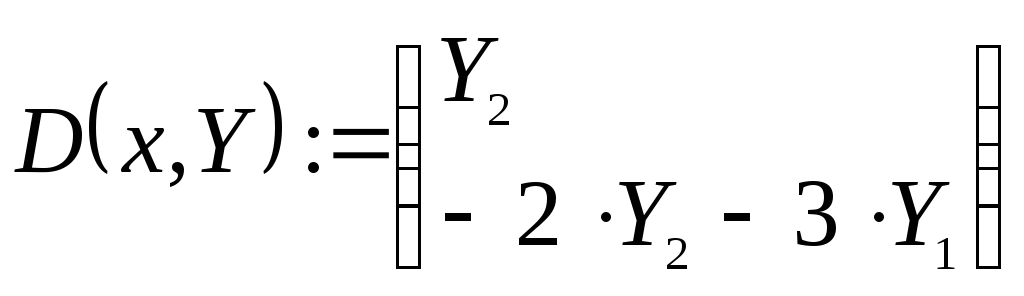
4)
-
решение в форме матрицы, I-й
столбец которой состоит из значений
,II-й
из значений
,III-й
-
.
5) построить график решения
Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
Структура
общего решения ДУ
зависит от характера корней соответствующего
характеристического уравнения:
.
Если
характеристическое уравнение имеет 2
различных действительных корня
и
,
то фундаментальная система решений
имеет вид
и
.
Если характеристическое уравнение
имеет 2 равных действительных корня
,
то фундаментальная система решений
имеет вид
и
.
Если характеристическое уравнение
имеет 2 комплексных корня
и
,
то фундаментальная система решений
имеет вид
и
.
Общее
решение ДУ:
.
Задача
4.
Найдите общее решение уравнения
.
Решите задачу Коши с начальными условиями
,
,
(решенную приближенно методом Рунге-Кутта
в задаче 3). Проверьте правильность
решения. Изобразите его график.
Решение:
1) Установите режим автоматических вычислений.
2)
3) Найдите корни характеристического уравнения:
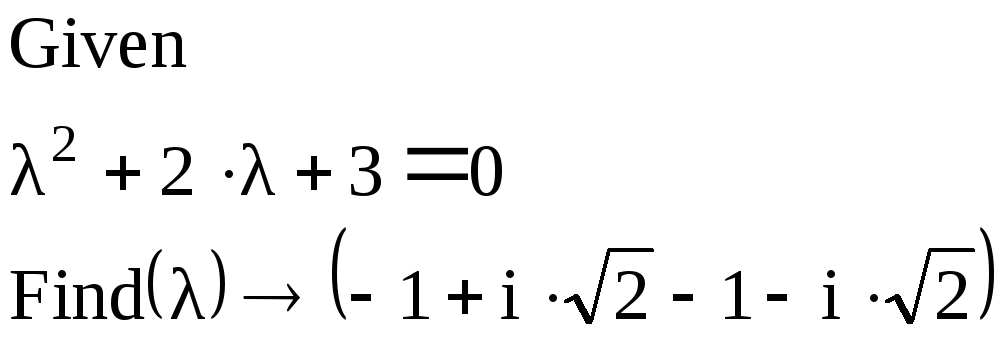
4)
- функции фундаментальной системы
решений.
5)
Запишите общее решение уравнения (как
функцию переменных
,
и
):
6)
Для определения значений
и
,
при которых выполняются начальные
условия, найдите
и
:
Упростим
это выражение:
.
7)
Используйте вычислительный блок для
нахождения
и
,
учитывая, что
Given
=
=
Таким образом, искомое решение:
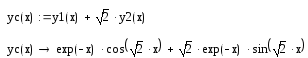
8) Проверьте решение подстановкой в уравнение:
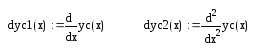
9) Проверьте выполнение начальных условий:
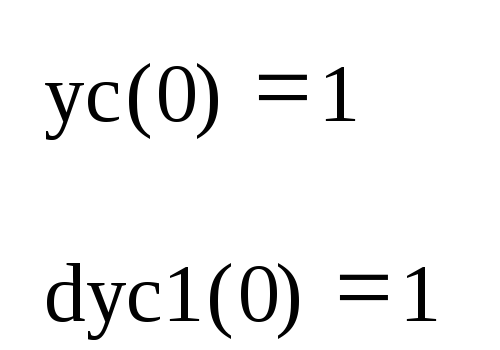
10) Постройте график решения:
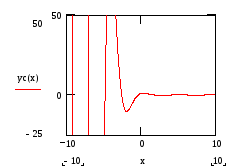
11) Сравните графики точного и приближенного решений.
Линейные неоднородные ду 2-го порядка с постоянными коэффициентами и правой частью специального вида
Общее решение линейного неоднородного уравнения записывается как сумма общего решения однородного уравнения и любого частного решения неоднородного уравнения.
Вид частного решения устанавливается по виду правой части уравнения:
,
при этом
1)
для
,
если
,
то частное решение ДУ имеет вид
.
Если
или
,
то частное решение ДУ
.
Если
то
частное решение ДУ
.
2)
для
,
если
,
то частное решение ДУ имеет вид
.
Если
или
,
то частное решение ДУ
.
Если
,
то частное решение ДУ
.
3)
для
(в
частности, при
или
).
Если
,
то частное решение ДУ имеет вид
.
Если
или
,
то частное решение ДУ имеет вид
.
Задача
5.
Найдите общее решение неоднородного
уравнения
.
Проверьте правильность решения.
Решение:
1)
2-3) Найдите общее решение соответствующего однородного уравнения вашего задания (см. пункты 2-5 решения задачи 4).
4)
Запишите выражение для частного решения
как функцию переменной
и неизвестных коэффициентов – по виду
правой части неоднородного уравнения:
5) Подставьте выражение частного решения в левую часть уравнения:
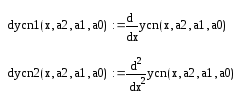
6)
В полученном выражении приведите
подобные относительно степеней
,
для чего выделите переменную х и щелкните
по строкеCollect
в меню Symbolics:
7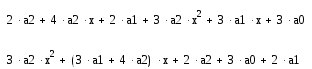
)
Приравняв коэффициенты при степенях
полученного выражения левой части
уравнения и выражения правой части,
запишите и решите систему относительно
параметров
,
,
:
=
=0
=
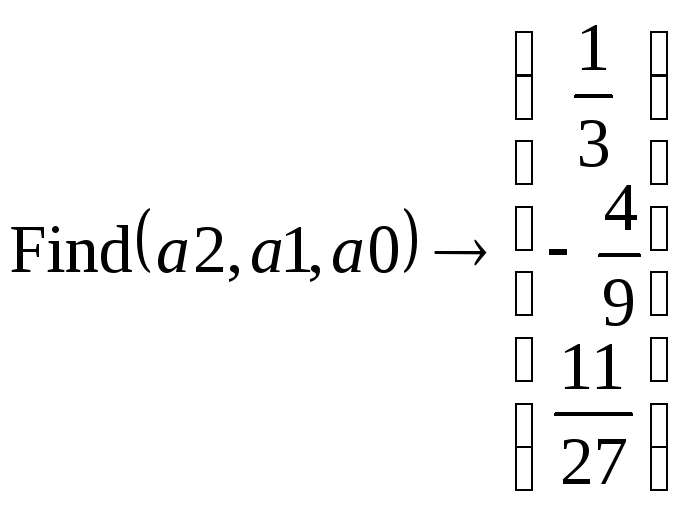
8)
Запишите частное решение с найденными
коэффициентами
,
,
:
9) Запишите общее решение неоднородного уравнения:
10) Проверьте решение подстановкой:
Замечание.
В задаче 5 правая часть имеет вид
многочлена
.
Если в задании
или
,
соответственно измените в решении
пункты 4-9.