Задание 7.4.

По заданной функции распределения F(x) случайной величины СВ X найти плотность распределения и построить ее график. Вычислить вероятность P(a≤X≤b) попадания значения СВ в заданный интервал, математическое ожидание и дисперсию.

.

.

.

.

.

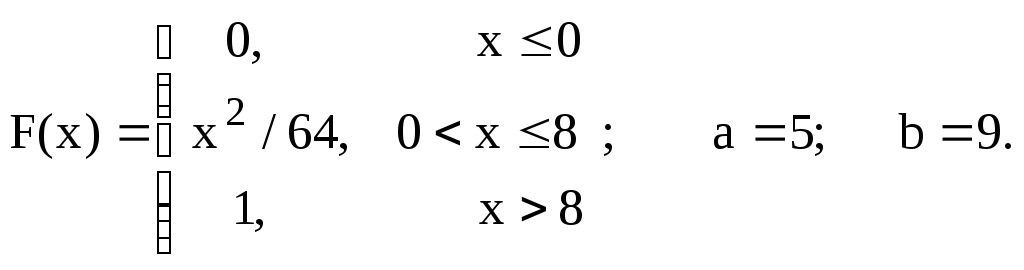
6.

7.

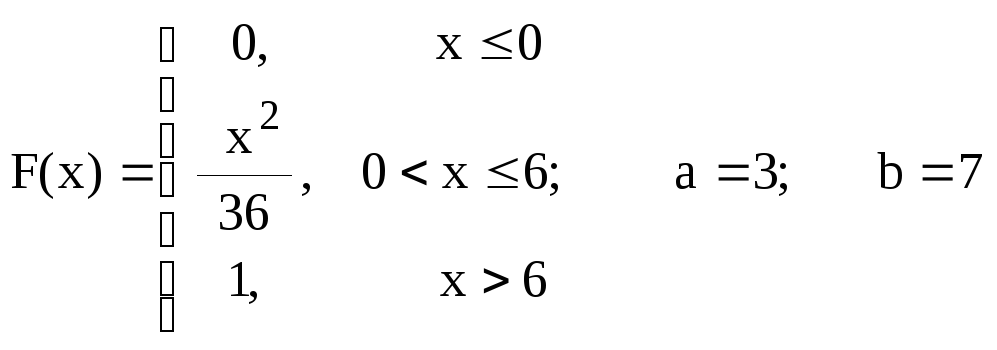
8.

9.

10.

11.

12.

13.

14.

15.

16.

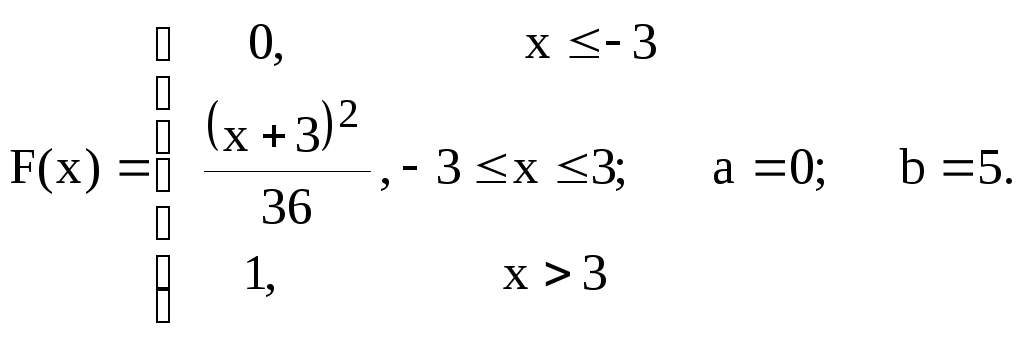
17.

18.

19.

20.

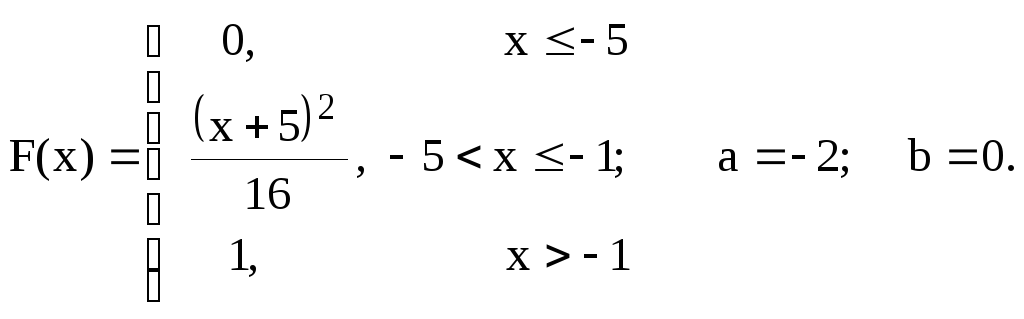
21.

22.

23.

24.

25.

26.

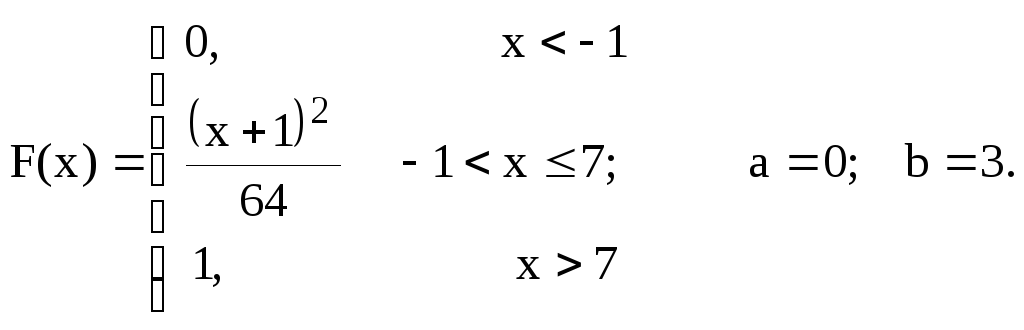
27.

28.

29.

30.

Задание 7.5.

Найти вероятность попадания в заданный интервал [a,b] значения нормально распределенной случайной величины X, если известно её математическое ожидание M[X] и дисперсия D[X].

Вар.	M[X]	D[X]		b
1	10	16	2	13
2	9	25	5	14
3	8	1	6	9
4	7	4	3	10
5	6	9	2	11
6	5	1	5	7
7	4	25	2	7
8	3	4	3	10
9	2	25	4	9
10	2	16	6	10
11	10	4	9	12
12	9	16	5	12
13	8	4	4	10
14	7	9	4	11
15	6	4	3	10
16	5	4	2	7
17	3	1	2	5
18	4	1	3	7
19	2	9	-2	4
20	0	16	-1	3
21	5	9	4	9
22	6	4	4	10
23	8	9	0	9
24	7	16	-1	20
25	-8	9	-9	0
26	2	9	-2	4
27	7	36	0	9
28	8	25	2	10
29	1	9	-1	5
30	4	9	0	9

Задание 7.6.

В партии из n изделий каждое может оказаться стандартным с вероятностью p. С помощью локальной и интегральной формул Муавра-Лапласа вычислить вероятность того, что число стандартных деталей в партии будет: а) равно m; б) заключено между m₁ и m₂.

Вар.	p	n	m	m1	m2
1	0.3	100	32	25	35
2	0,7	400	287	270	290
3	0,5	300	143	145	160
4	0,4	350	137	135	155
5	0,6	600	365	340	365
6	0,2	850	166	145	185
7	0,4	900	362	340	375
8	0,6	750	447	435	470
9	0,3	150	47	40	55
10	0,8	100	76	75	90
11	0,3	400	116	100	130
12	0,7	200	145	130	150
13	0,2	450	86	80	95
14	0,1	900	96	80	100
15	0,5	750	381	355	385
16	0,4	750	294	285	320
17	0,6	200	125	110	135
18	0,2	600	112	105	135
19	0,3	400	127	110	130
20	0,1	700	64	55	80
21	0,7	650	450	445	480
22	0,5	300	155	140	160
23	0,6	450	262	255	280
24	0,8	200	163	145	165
25	0,1	400	44	35	55
26	0,3	500	147	130	165
27	0,2	200	43	30	50
28	0,4	650	250	245	270
29	0,6	300	185	175	195
30	0,5	500	243	235	265