1.5. Контрольное задание

Из генеральной совокупности извлечена выборка, представленная в виде статистического ряда. Требуется для выборки, соответствующей номеру варианта:

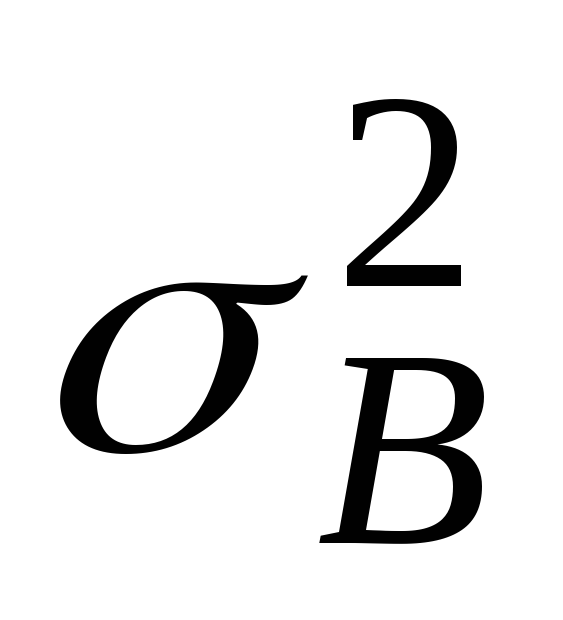1. вычислить выборочное среднее , выборочную дисперсию, исправленную выборочную дисперсию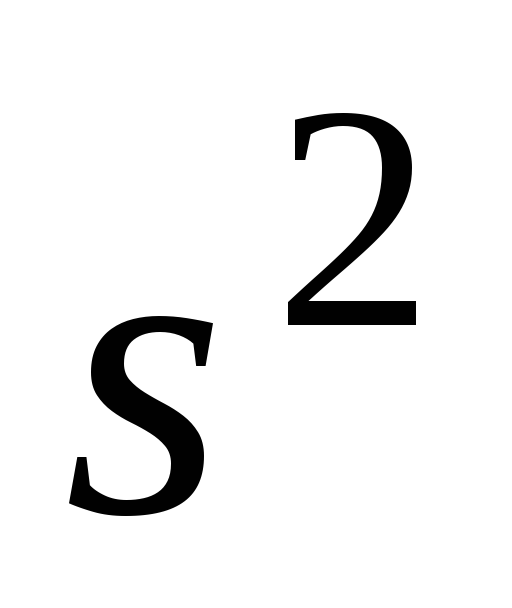и среднее квадратичное отклонение;

2. найти с доверительной вероятностью 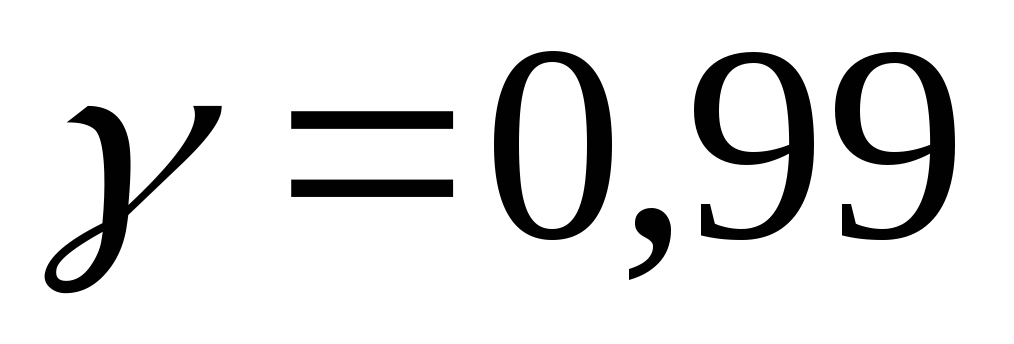доверительный интервал для математического ожидания, а также доверительный интервал для;

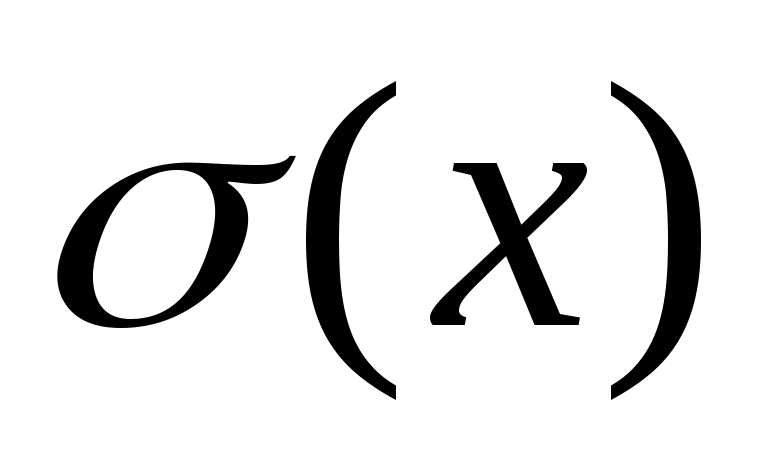3. найти размах варьирования и среднее абсолютное отклонение;

4. вычислить моду и медиану;

5. построить эмпирическую функцию распределения;

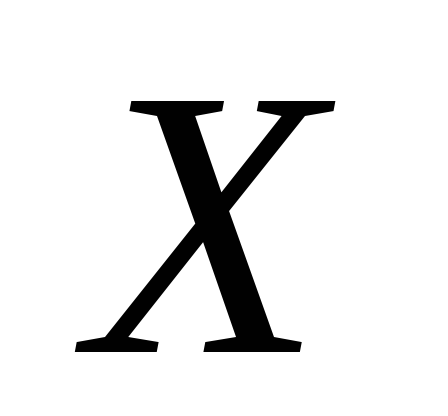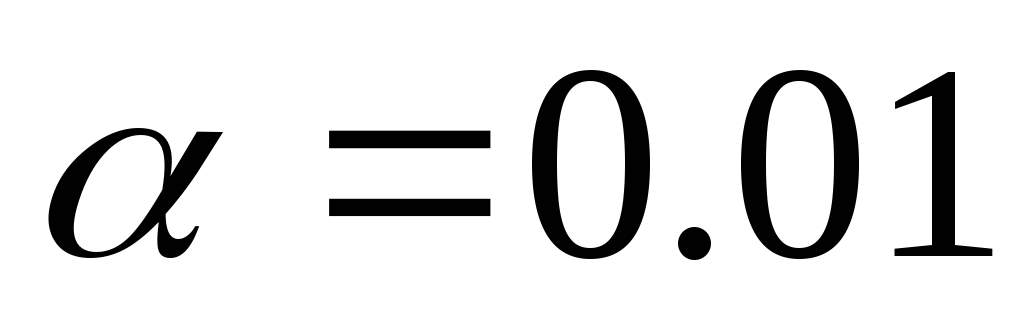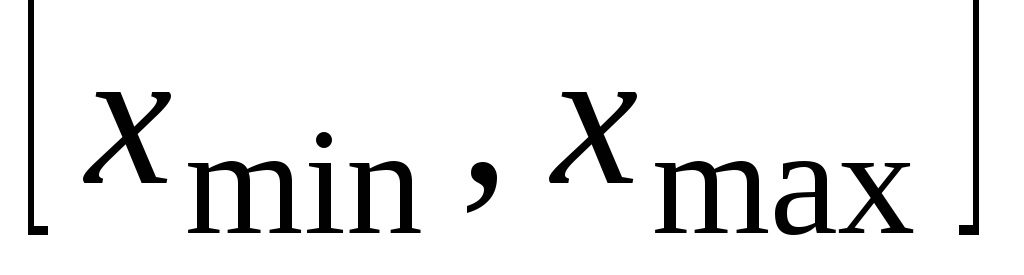6. проверить, согласуются ли выборочные данные с гипотезой о нормальном распределении СВ графически, с помощью асимметрии и эксцесса и с помощью критерия согласия Пирсона при уровне значимости, разбив отрезокна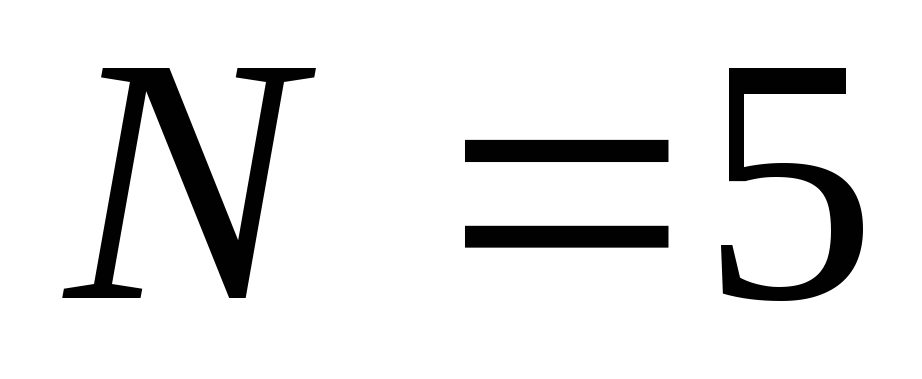интервалов одинаковой длины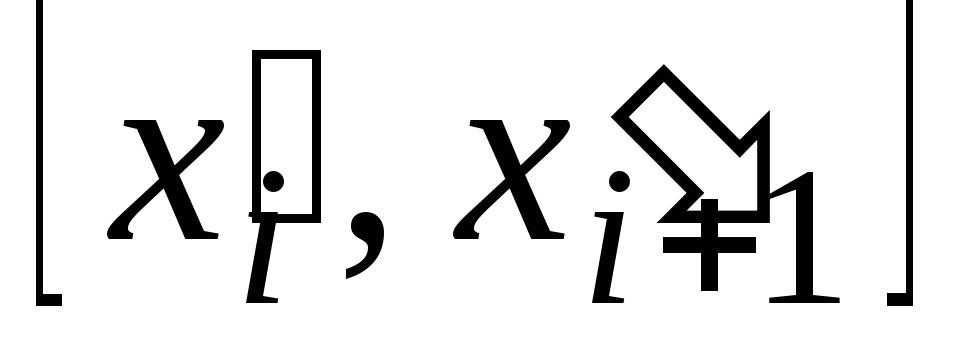с границами.

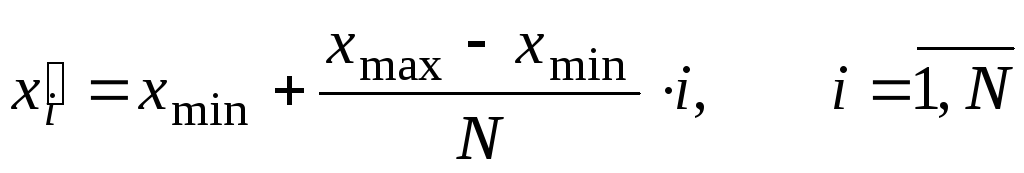1.6. Варианты заданий для самостоятельногорешения

1		80	90	100	110	120	130	140
		4	8	14	40	16	12	6
2		13	14	15	16	17	18	19
		7	16	40	25	7	5	3
3		21	28	35	42	49	56	63
		7	11	22	50	5	3	2
4		2	3	4	5	6	7	8
		4	11	25	30	15	10	5
5		20	26	32	38	44	50	56
		2	3	15	50	12	11	7
6		13	23	33	43	53	63	73
		3	17	25	40	8	4	3
7		30	35	40	45	50	55	60
		4	16	20	40	13	4	3
8		33	38	46	54	62	70	78
		7	11	12	60	5	3	2
9		12	15	22	25	30	35	40
		3	7	12	40	18	12	8
10		10	20	30	40	50	60	70
		4	11	25	30	15	10	5

П р а к т и ч е с к о е з а н я т и е № 2 корреляционный и регрессионный анализ

2.1. Линейная регрессия

Пусть изучается система количественных признаков . В результатенезависимых опытов полученыпар чисел

Найдем по данным наблюдений выборочное уравнение прямой линии среднеквадратичной регрессии. Для определенности будем искать уравнение регрессии на:

.

Поскольку различные значения признакаи соответствующие им значенияпризнаканаблюдались по одному разу, то группировать данные нет необходимости. Также нет надобности использовать понятие условной средней, поэтому искомое уравнение можно записать так:

.

Угловой коэффициент прямой линии регрессии наназываютвыборочным коэффициентом регрессии на и обозначают через ; он является оценкой коэффициента регрессии.

Итак, будем искать выборочное уравнение прямой линии регрессии навида

(2.1)

Подберем параметры иb так, чтобы точки, построенные по данным наблюдений, на плоскости лежали как можно ближе к прямой. Уточним смысл этого требования. Назовем отклонением разность

, ,

где – вычисленная по уравнению (2.1) ордината, соответствующая наблюдаемому значению– наблюдаемая ордината, соответствующая.

Подберем параметры иb так, чтобы сумма квадратов отклонений была минимальной (в этом состоит сущность метода наименьших квадратов). Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений есть функция этих параметров (временно вместобудем писать):

, или .

Для отыскивания минимума приравняем нулю соответствующие частные производные:

, .

Выполнив элементарные преобразования, получим систему двух линейных уравнений относительно и:

;(2.2)

Решив эту систему, найдем искомые параметры:

(2.3)

Аналогично можно найти выборочное уравнение прямой линии регрессии на:

,

где – выборочный коэффициент регрессиина.

Пример 1. Найти выборочное уравнение прямой линии регрессии на.

Опытные данные представлены в таблице:

x	-2	-1	0	1	2	3
y	-0,4	0,2	0,7	1,6	2,0	3,5

Проверить адекватность полученной модели.

Решение.

1) Множество точек, заданных таблицей, построим на плоскости (рис. 2.1).

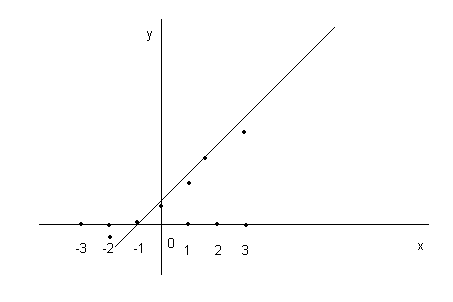
Рис. 2.1.

Из рисунка видно, что точки группируются около некоторой прямой. Следовательно, зависимость между переменнымиx и y близка к линейной. Найдем методом наименьших квадратов эмпирическую формулу вида .

2) Определим модель. Для вычисления коэффициентов a и b воспользуемся таблицей:

№
1	-2	-0,4	4	0,16	0,8
2	-1	0,2	1	0,04	-0,2
3	0	0,7	0	0,49	0
4	1	1,6	1	2,56	1,6
5	2	2,0	4	4	4,0
6	3	3,5	9	12,25	10,5
СУММА		7,6	19	19,5	16,7

Напишем нормальную систему уравнений (2.2): 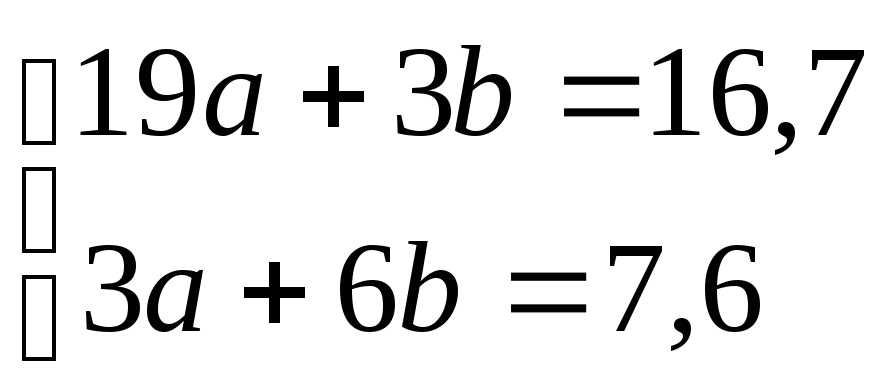. Из этой системы уравнений найдем а=0,74 иb=0,90. Следовательно, модель имеет вид .