
- •Кафедра высшей математики № 1
- •Содержание
- •Программа Ряды
- •IИнтегральное исчисление функций нескольких переменных
- •Элементы операционного исчисления
- •1. Ряды
- •1.1. Числовые ряды. Основные определения. Признаки сравнения
- •1.2. Достаточные признаки сходимости рядов с положительными членами
- •1.3. Знакопеременные ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница
- •1.4. Функциональные ряды. Область сходимости функционального ряда. Степенные ряды
- •1.5. Разложение функции в ряд Тейлора
- •1.6. Применение степенных рядов в приближенных вычислениях
- •1. Приближенное вычисление значений функций.
- •2. Приближенное вычисление определенных интегралов.
- •3. Интегрирование дифференциальных уравнений с помощью рядов.
- •1.7. Ряд Фурье функции, заданной на отрезке длиной 2
- •1.8. Ряд Фурье функции, заданной на отрезке длиной 2l
- •2. Интегральное исчисление функций нескольких переменых
- •2.1. Определенный интеграл по фигуре. Основные понятия и свойства
- •2.2. Вычисление двойных и тройных интегралов в декартовых координатах
- •2.3. Замена переменных в кратном интеграле
- •2.4. Криволинейные интегралы I и II рода
- •2.5. Поверхностные интегралы I и II рода
- •2.6. Вычисление криволинейных интегралов I и II рода
- •2.7. Вычисление поверхностных интегралов I и II рода. Связь между ними
- •2.8. Формулы Грина, Стокса, Остроградского-Гаусса
- •3. Элементы операционного исчисления
- •3.1. Оригинал и его изображения
- •3.2. Основные теоремы операционного исчисления
- •1. Теорема линейного изображения.
- •3.3. Отыскание оригинала по изображению
- •3.4. Решение дифференциальных уравнений и систем дифференциальных уравнений операционным методом
- •Контрольная работа №3
- •111-120. Вычислить работу силового поля при перемещении материальной точки вдоль пути
1.4. Функциональные ряды. Область сходимости функционального ряда. Степенные ряды
Ряд вида ![]() ,
членами которого являются функции
,
членами которого являются функции ![]() ,
называется функциональным.
,
называется функциональным.
Множество всех действительных значений аргумента x, для которых функциональный ряд
![]() (10)
(10)
становится сходящимся числовым
рядом, называется областью
сходимости этого ряда.
Функция ![]() ,
где
,
где ![]() ,
а x принадлежит
области
сходимости, называется суммой
ряда, функция
,
а x принадлежит
области
сходимости, называется суммой
ряда, функция ![]() – остатком функционального
ряда.
– остатком функционального
ряда.
Для определения области сходимости ряда (10) можно использовать известные признаки сходимости числовых рядов, считая x фиксированным.
Функциональный ряд (10)
называется равномерно
сходящимся на промежутке
p R,
если для любого >0
существует номер no,
не зависящий от x, что
для всех n >no
и для всех x p
выполняется неравенство ![]() ,
то есть
,
то есть ![]() ,
где Rn(x)
– остаток ряда.
,
где Rn(x)
– остаток ряда.
Признак Вейерштрасса.
Если |un(x)|Cn,
(n=1,2,...) при ![]() и числовой ряд
и числовой ряд ![]() сходится, то функциональный ряд (10)
сходится на отрезке [a,b]
абсолютно и равномерно.
сходится, то функциональный ряд (10)
сходится на отрезке [a,b]
абсолютно и равномерно.
Теорема 4.
Если члены сходящегося ряда (10) имеют
непрерывные производные при ![]() и ряд из производных
и ряд из производных ![]() сходится равномерно на [a,b],
то ряд (10) можно дифференцировать
почленно:
сходится равномерно на [a,b],
то ряд (10) можно дифференцировать
почленно:
![]() .
.
Теорема 5. Если
члены ряда (10) непрерывны на [a,b]
и этот ряд сходится равномерно на отрезке
[a,b],
то ряд (10) можно
интегрировать
почленно:
![]() .
.
Степенным рядомназывается функциональный ряд вида
![]() ,
(11)
,
(11)
где Cn и a – действительные числа. Область сходимости степенного ряда (11) имеет один из следующих видов:
(a -R ,a +R), [a -R ,a +R), (a -R ,a +R], [a -R ,a +R].
Число R
называется радиусом
сходимости, а интервал
(a -R ,a +R)
– интервалом сходимости
степенного ряда (11). Радиус сходимости
можно находить по формулам:
![]() ,
если
эти пределы существуют. В частных случаях
R может быть равен 0
или .
,
если
эти пределы существуют. В частных случаях
R может быть равен 0
или .
Вопрос о сходимости степенного ряда (11) в концевых точках области сходимости, то есть при x =a -R, x =a +R, исследуется особо (с применением известных признаков сходимости числовых рядов).
Ряды, полученные почленным дифференцированием и интегрированием степенного ряда, имеют тот же радиус и интервал сходимости, и их сумма внутри интервала сходимости равна соответственно производной и интегралу от суммы первоначального ряда.
Пример 1. Найти
область сходимости ряда ![]() .
.
Решение.
При фиксированном x
этот ряд – знакоположительный. Применим
к нему признак Коши. Найдем предел ![]() ;
l<1 - при
;
l<1 - при ![]() <1,
т.е. при x <0.
При l =1,
т.е. при x =0
данный функциональный ряд станет рядом
<1,
т.е. при x <0.
При l =1,
т.е. при x =0
данный функциональный ряд станет рядом
![]() .
Общий член ряда
.
Общий член ряда ![]() при n
стремится
к числу e,
и поэтому ряд расходится (не выполнен
необходимый признак
сходимости). Итак, область сходимости
данного ряда
(-,0).
при n
стремится
к числу e,
и поэтому ряд расходится (не выполнен
необходимый признак
сходимости). Итак, область сходимости
данного ряда
(-,0).
Пример 2.
Можно ли почленно дифференцировать ряд
![]() в области его сходимости?
в области его сходимости?
Решение.
Областью сходимости данного ряда
является вся числовая ось R=(-,+),
так как для любого xR
верно неравенство ![]() ,
а ряд
,
а ряд ![]() сходится. Члены исходного ряда имеют
непрерывные производные
сходится. Члены исходного ряда имеют
непрерывные производные ![]() ,
ряд из производных
,
ряд из производных ![]() сходится равномерно на R
по признаку Вейерштрасса. Действительно,
верны неравенства
сходится равномерно на R
по признаку Вейерштрасса. Действительно,
верны неравенства ![]() ,
а ряд
,
а ряд ![]() сходится. По теореме 4 исходный ряд можно
почленно дифференцировать в области R
его сходимости, т.е.
сходится. По теореме 4 исходный ряд можно
почленно дифференцировать в области R
его сходимости, т.е.
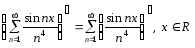 .
.
Пример 3.
Найти область сходимости степенного
ряда ![]() .
.
Решение.Находим
радиус сходимости ряда. ![]()
![]() .
Это означает, что исходный ряд сходится
абсолютно при
.
Это означает, что исходный ряд сходится
абсолютно при ![]() .
Далее, исследуем сходимость ряда при x
= 1.
Если x =
1, то данный ряд становится гармоническим
рядом
.
Далее, исследуем сходимость ряда при x
= 1.
Если x =
1, то данный ряд становится гармоническим
рядом ![]() ,
который расходится.
Если x =–1,
то получаем знакочередующийся ряд
,
который расходится.
Если x =–1,
то получаем знакочередующийся ряд ![]() ,
который сходится по признаку Лейбница.
Следовательно, областью сходимости
ряда является полуинтервал [-1,1).
При
,
который сходится по признаку Лейбница.
Следовательно, областью сходимости
ряда является полуинтервал [-1,1).
При ![]() ряд сходится абсолютно, при
ряд сходится абсолютно, при ![]() – условно.
– условно.
Пример 4.Найти сумму ряда
.
Решение. Обозначим искомую сумму ряда через S(x), т.е.
![]() .
(12)
.
(12)
Можно проверить, что исходный
ряд при ![]() сходится абсолютно. Дифференцируем
почленно равенство (12):
сходится абсолютно. Дифференцируем
почленно равенство (12):
![]() (применена
формула суммы членов убывающей
геометрической прогрессии).
Отсюда,
интегрируя и учитывая, что S(0)=0,
находим
(применена
формула суммы членов убывающей
геометрической прогрессии).
Отсюда,
интегрируя и учитывая, что S(0)=0,
находим
Пример 5.Найти сумму ряда
.
Решение.
Обозначим эту сумму ряда через S(x),
т.е. . Данное равенство
перепишем так: S(x)=xQ(x),
где ![]() .
Почленное интегрирование последнего
равенства приводит к сумме членов
убывающей геометрической прогрессии:
.
Почленное интегрирование последнего
равенства приводит к сумме членов
убывающей геометрической прогрессии:
Отсюда найдем Q(x):
![]() ,
поэтому искомая сумма S(x)
такова:
,
поэтому искомая сумма S(x)
такова: ![]() .
.
