Контрольная работа №3
1-20. Пользуясь известными признаками сходимости, исследовать на сходимость ряды.
1. а) 
б)
2. а) 
б)
3. а) 
б)
4. а) 
б)
5. а) 
б)
6. а) 
б)
7. а) 
б)
8. в) 
б)
9. а) 
б)
10. а) 
б)
11. а) 
б)
12. а) 
б)
13. а) 
б)
14. а) 
б)
15. а) 
б)
16. а) 
б)
17. а) 
б)
18. а) 
б)
19. а) 
б)
20. а) 
б)
21-40. Найти область сходимости степенного ряда.
21. 
22.
23. 
24.
25. 
26.
27. 
28.
29. 
30.
31. 
32.
33. 
34.
35. 
36.
37. 
38.
39. 
40.
41-50. С помощью разложения подынтегральной функции в ряд вычислить определенный интеграл с точностью до =0,001.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51-60. Найти первые четыре (отличные от нуля) члена разложения в степенной ряд решения дифференциального уравнения, удовлетворяющего начальным условиям.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61-80. Вычислить с помощью двойного интеграла площадь плоской области D, ограниченной заданными линиями:
D:
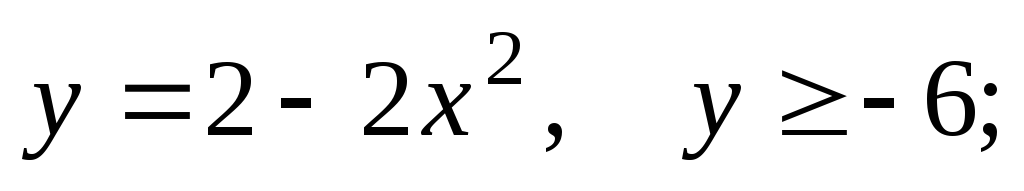
D:
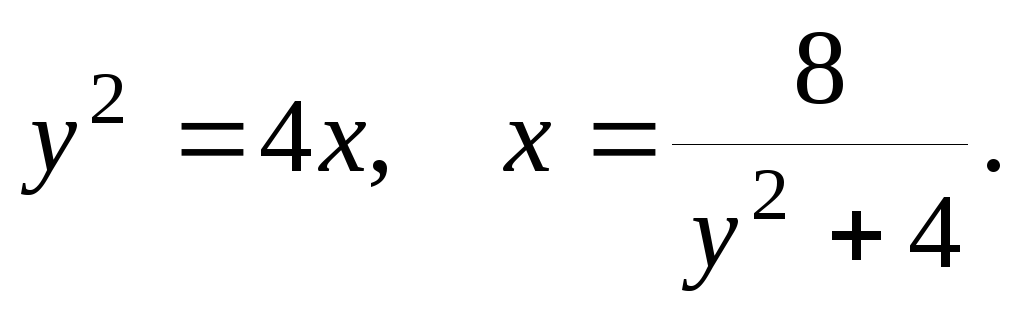
D:
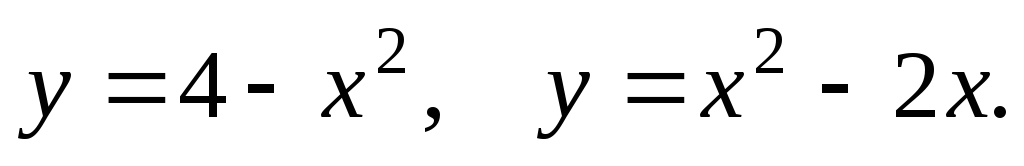
D:
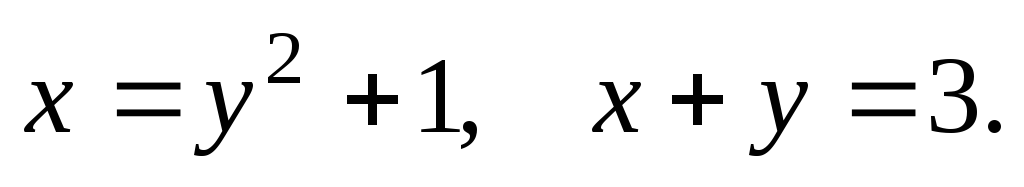
D:
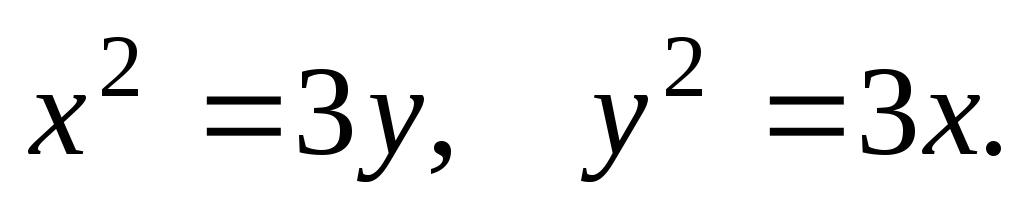
D:
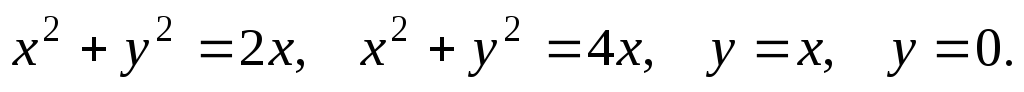
D:
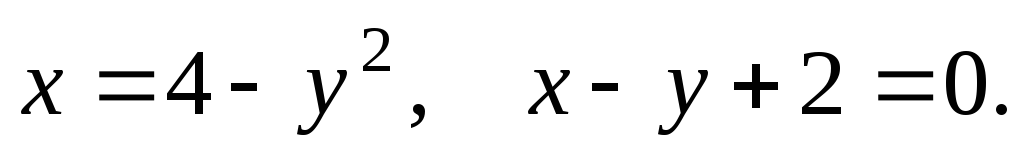
D:
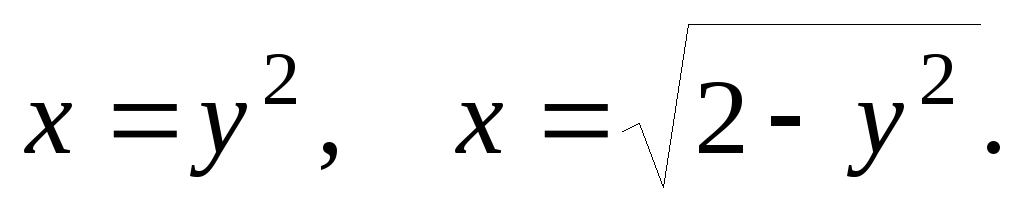
D:
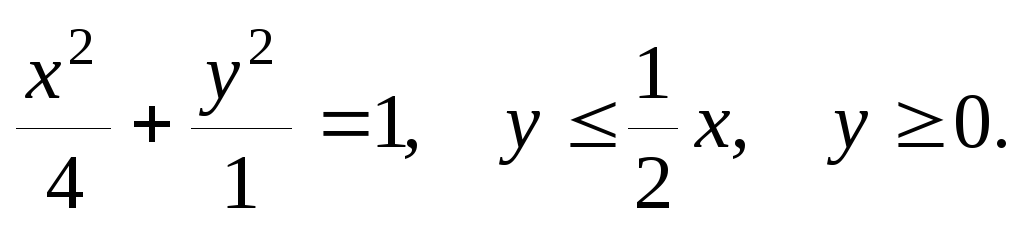
D:
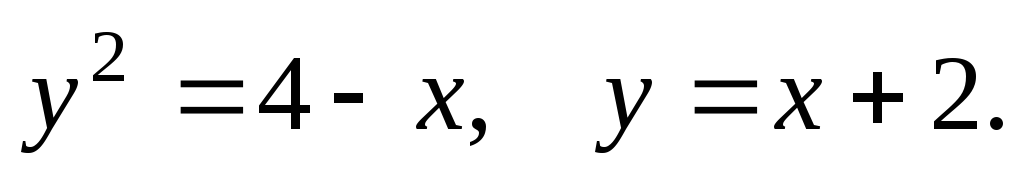
D:
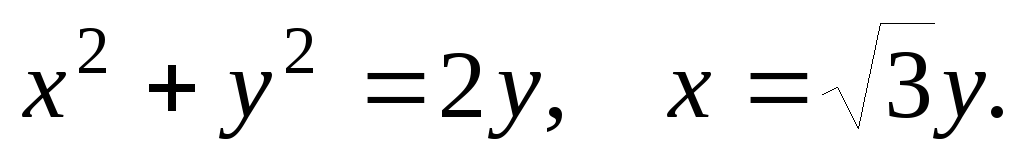
D:
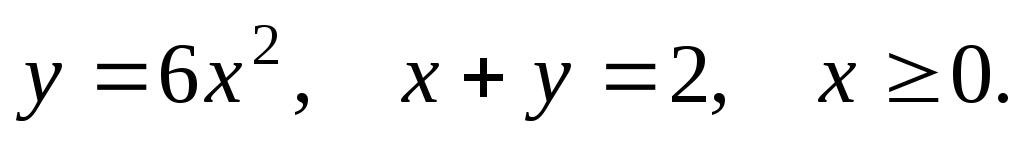
D:
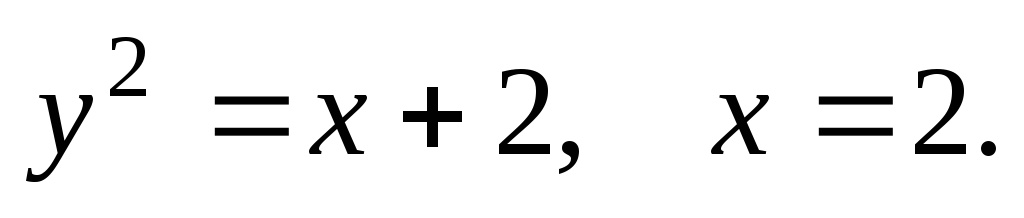
D:
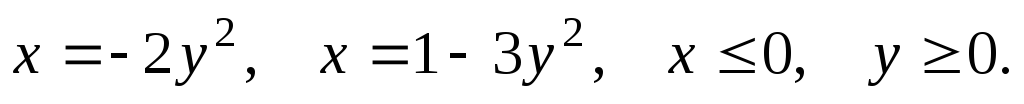
D:
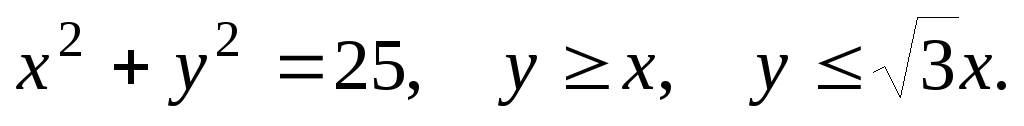
D:
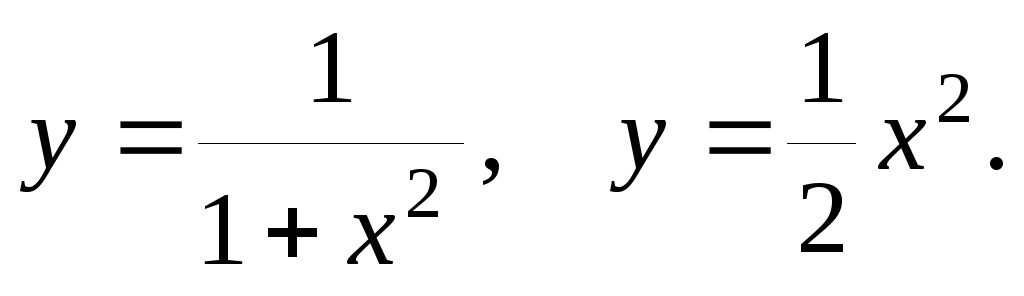
D:
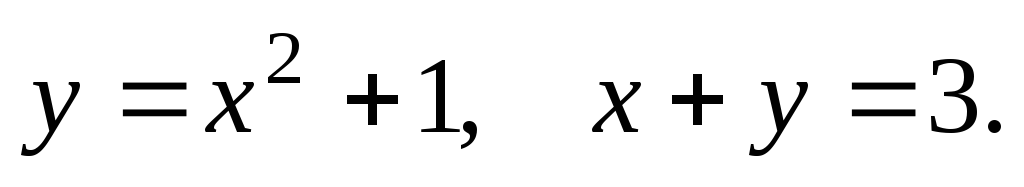
D:
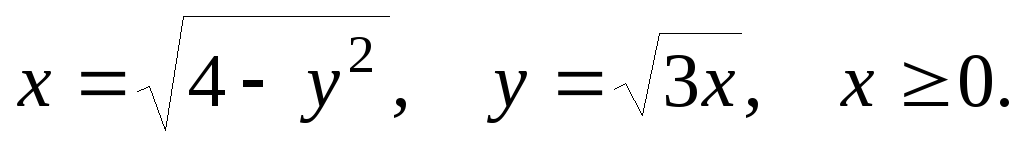
D:
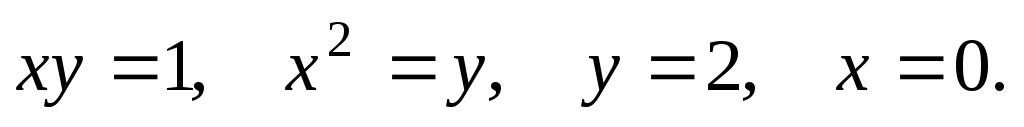
D:
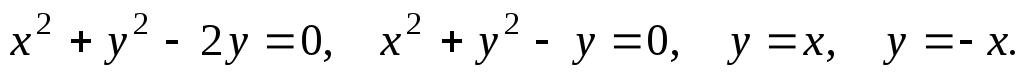
81-90. Вычислить объем тела, ограниченного заданными поверхностями:
91-100. Вычислить массу тела
V, ограниченного
заданными поверхностями (
– плотность в точке М
(x,
y, z)).
101-110. Найти массу, где
–
плотность:
отрезка АВ, где А(1,2); В(2,4), если плотность в каждой его точке равна произведению квадратов координат этой точки;
верхней половины кардиоиды
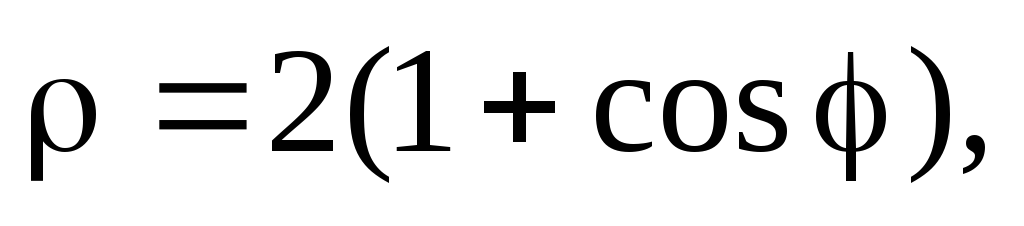если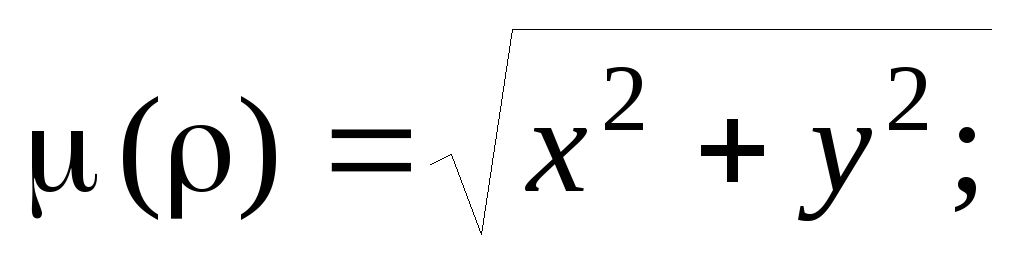
дуги кривой
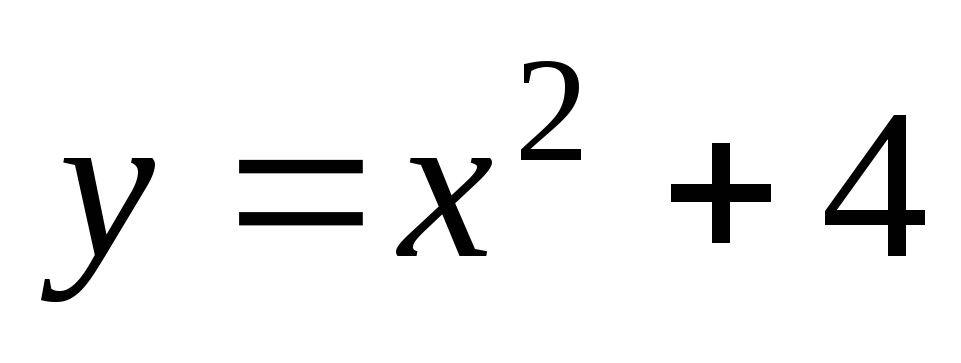от точки А(0,4)
до В(2,8),
если плотность в каждой точке ее равна
абсциссе точки;дуги лемнискаты
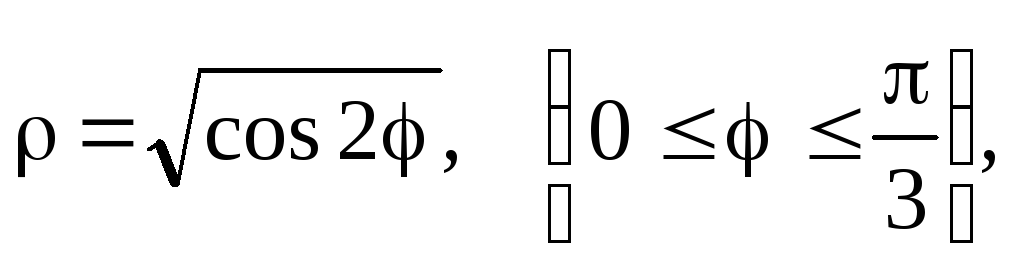если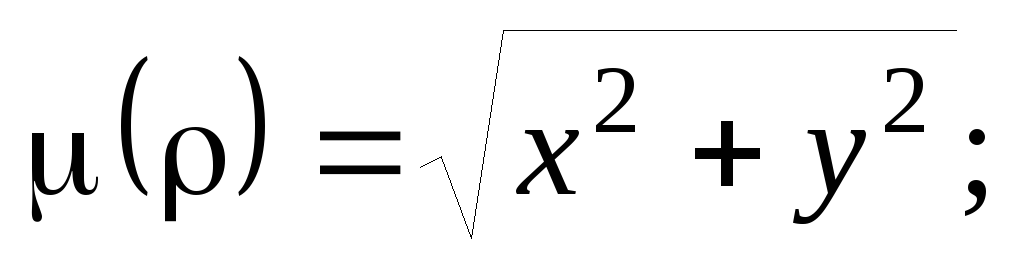
дуги синусоиды
,
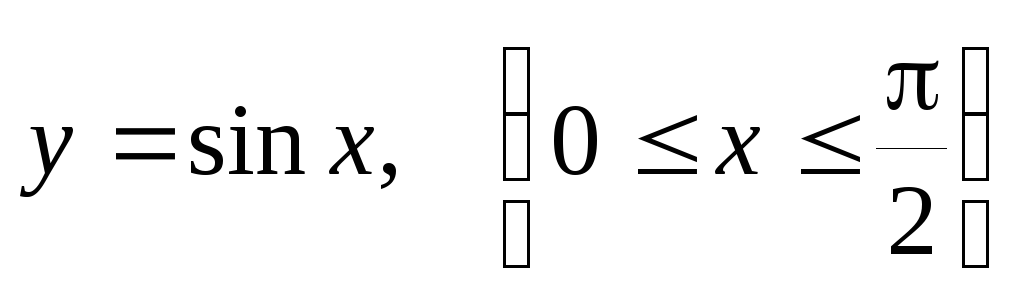если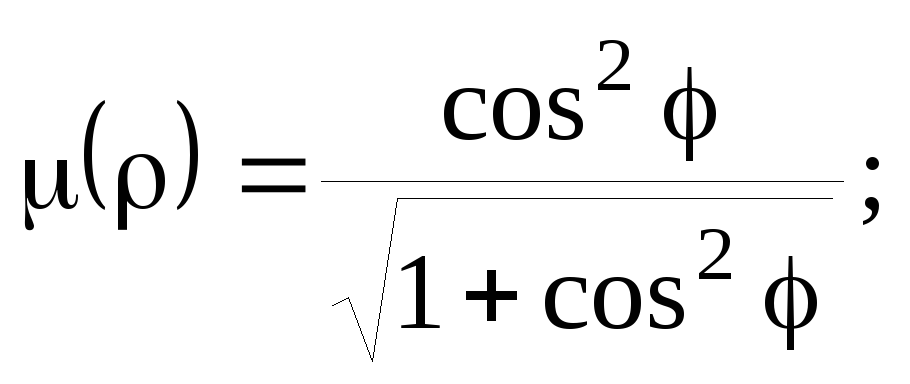
дуги окружности
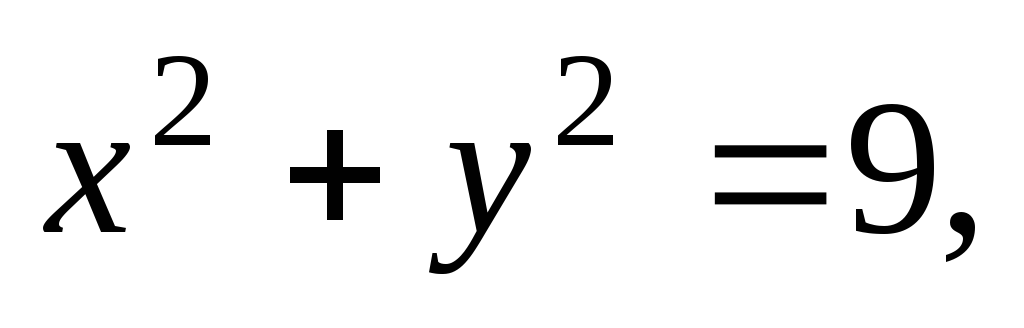лежащей в первой четверти, если плотность
в каждой ее точке равна абсциссе точки;дуги кривой
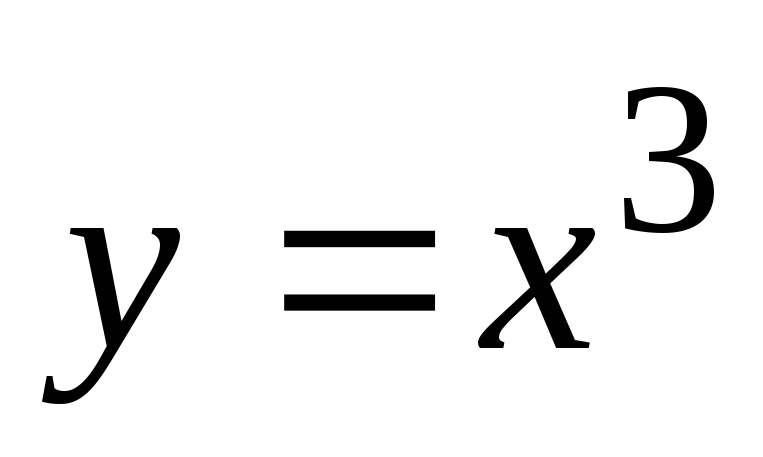от точки А(1;1)
до точки В(2;8),
если плотность в каждой точке кривой
равна ординате этой точки;дуги окружности
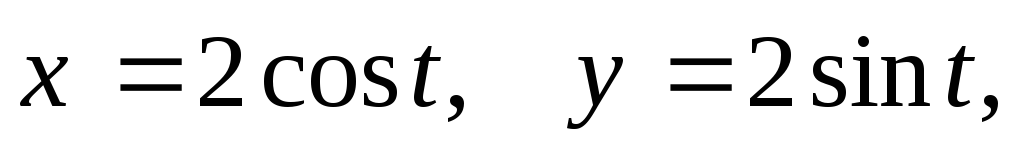лежащей в первой четверти, если плотность
ее в каждой точке равна произведению
абсциссы на квадрат ординаты этой
точки;одной арки циклоиды
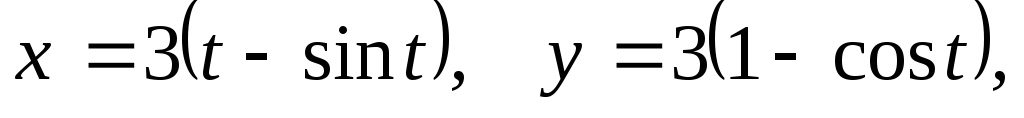если плотность ее в каждой точке равна
ординате точки;дуги тангенсоиды
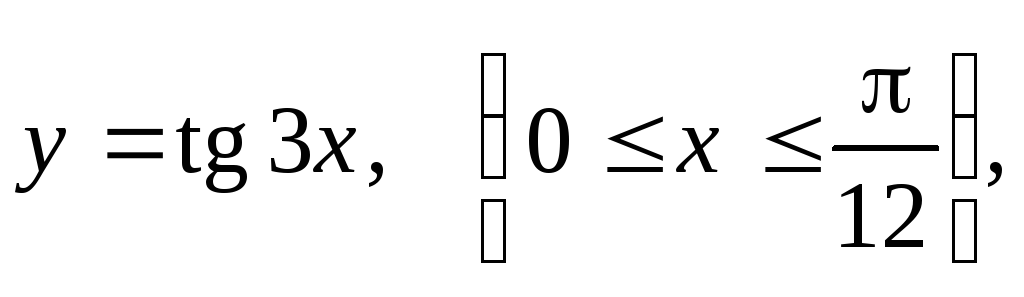если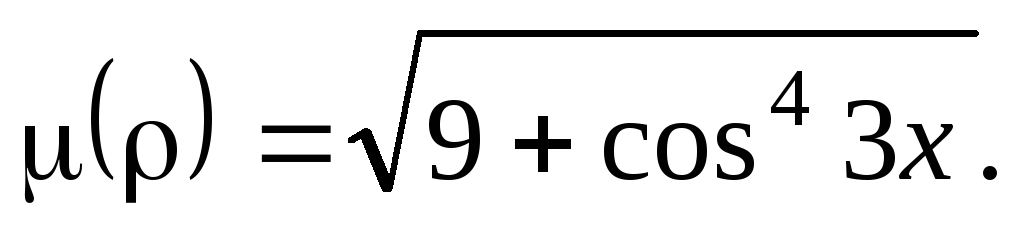
111-120. Вычислить работу силового поля при перемещении материальной точки вдоль пути
111. 
,
А (0;1;0);
В
112. 
В 
113. 
отрезок прямой,
В 
114.
В 
115. 
отрезок
прямой,
В 
116. 
В 
117. 
отрезок
прямой,
В 
118. 
В 
119. 
В 
120. 
В 
121-140. Решить уравнение или систему дифференциальных уравнений с заданными начальными условиями операционным методом.
121.
122.
123.
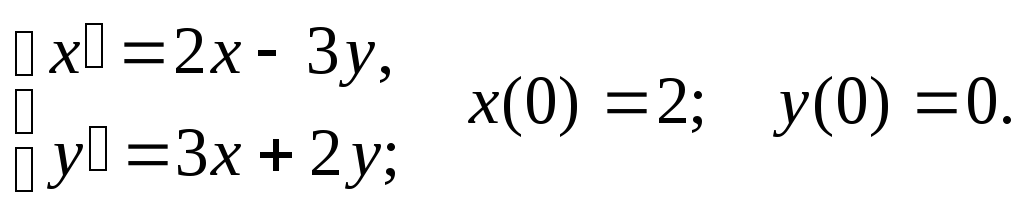
124.
125.
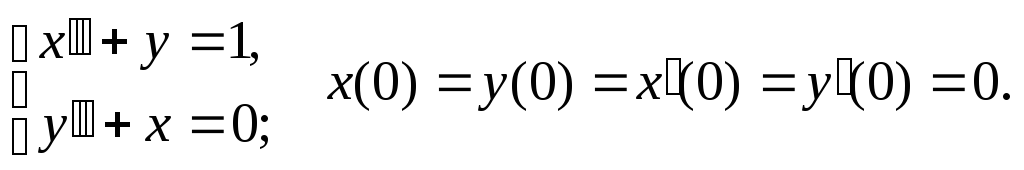
126.
127.
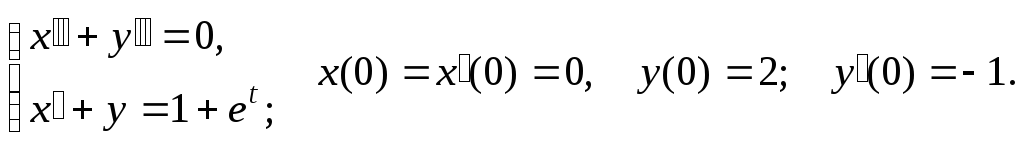
128.
129.
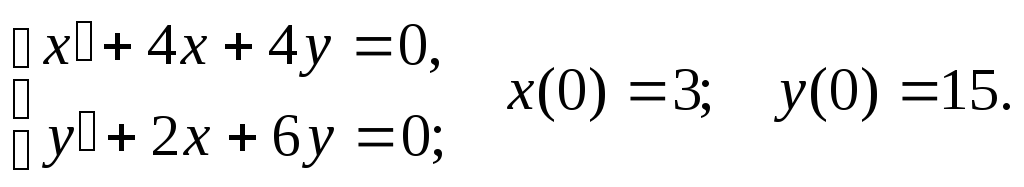
130.
131.
132.
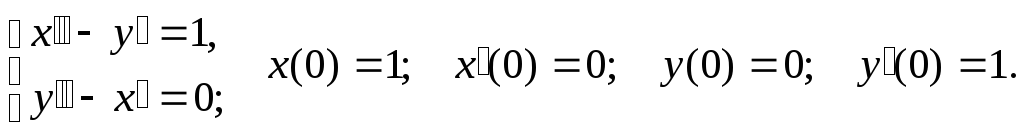
133.
134.
135.
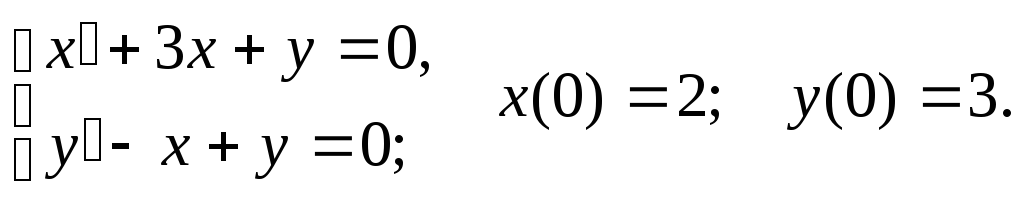
136. 
137. 
138. 
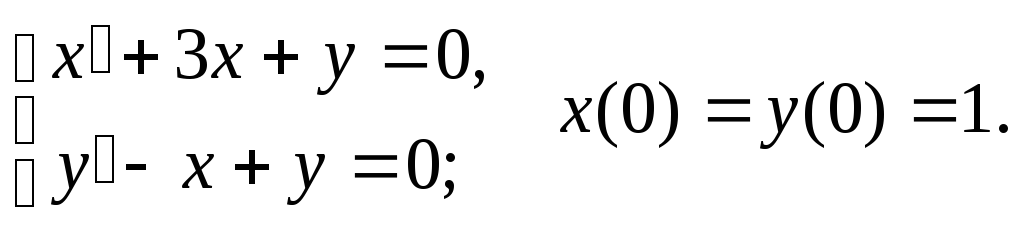
139.
140.
Рекомендуемая литература
Высшая математика для инженеров / С.А. Минюк [и др.]; под ред. Н.А. Микулика. – Минск: Элайда, 2007. – Т. 1, 2.
Пискунов, Н.С. Дифференциальное и интегральное исчисление (для втузов) / Н.С. Пискунов. – М.: Наука, 1978. – Т. 2, 3.
Бугров, Я.С. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я.С. Бугров, С.М. Никольский. – М.: Наука, 1981.
Щипачев, B.C. Высшая математика / B.C. Щипачев. – М.: Высш. шк., 1985.
Краснов, М.Л. Функции комплексного переменного. Операционное исчисление. Теория устойчивости (задачи и упражнения) / М.Л. Краснов, A.И. Киселев, Г.И. Макаренко. – М.: Наука, 1971.
Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высш. шк., 1980. – Ч. 2.
Герасимович, А.И. Математический анализ: справочное пособие: в 2 ч. / А.И. Герасимович. – Минск: Высш. шк., 1990. – Ч. 1.
Руководство к решению задач по высшей математике: учебное пособие: в 2 ч. / под общ. ред. Е.И. Гурского. – Минск: Высш. шк., 1990. – Ч. 2.
