1.3. Арифметические основы работы эвм

Двоичная система счисления получила широкое распространение с появлением ЭВМ. Любое число в этой системе представляется сочетанием нулей и единиц. Это позволяет достаточно просто организовать хранение и переработку информации, представленной в двоичном виде. Другим важным достоинством двоичной системы счисления является простота вычислений. Выполнение арифметических действий над числами в двоичной системе счисления производится по тем же правилам, что и в десятичной. При этом пользуются соответствующими таблицами. Рассмотрим только две арифметические операции: сложение и умножение, так как вычитание и деление по существу сводятся к сложению.

	0	1
0	0	0
1	0	1

+	0	1
0	0	1
1	1	10

Правила выполнения арифметических действий над двоичными числами можно свести в таблицу:

Сложение	Умножение
0 + 0 = 0	0 0 = 0
0 + 1 = 1	0 1 = 0
1 + 0 = 1	1 0 = 0
1 + 1 = 10	1 1 = 1

В устройствах, реализующих операцию арифметического сложения двоичных чисел, операнды представляют числами определенной разрядности (одинаковой для обоих операндов). При этом неиспользуемые разряды заполняются нулями. Это касается как целой, так и дробной частей числа.

В реальных ЭВМ чаще всего используются 16-, 32- и 64-разрядные числа. Однако для учебных целей при рассмотрении методов выполнения арифметических операций не будем обращать внимание на разрядность операндов (т. е. будем использовать разрядность, отличающуюся от разрядности реальных ЭВМ).

В двоичной системе счисления арифметическое сложение происходит по правилу сложения по модулю два с учетом переноса единицы в старший разряд.

Пример 13. Выполнить операцию арифметического сложения двоичных чисел 110111,01₂ и 10011,1₂.

Решение:

В качестве проверки воспользуемся десятичными числами, соответствующими исходным двоичным. При сложении дробей перенос осуществляется из дробной части числа в целую.

Умножение двоичных чисел производится путем образования частичных произведений и последующего их суммирования. Каждое частичное произведение равно 0, если в соответствующем разряде множителя стоит 0, или равно множимому, сдвинутому на соответствующее число разрядов влево, если в разряде множителя стоит 1.

Пример 14. Перемножить двоичные числа 111,1₂ и 101₂.

Решение:

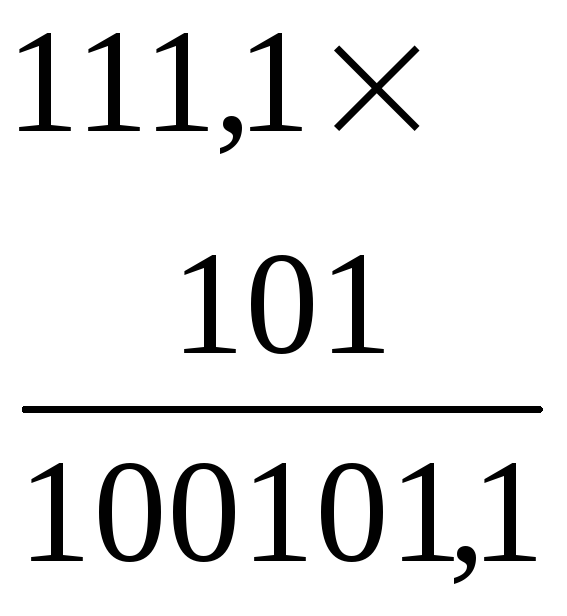
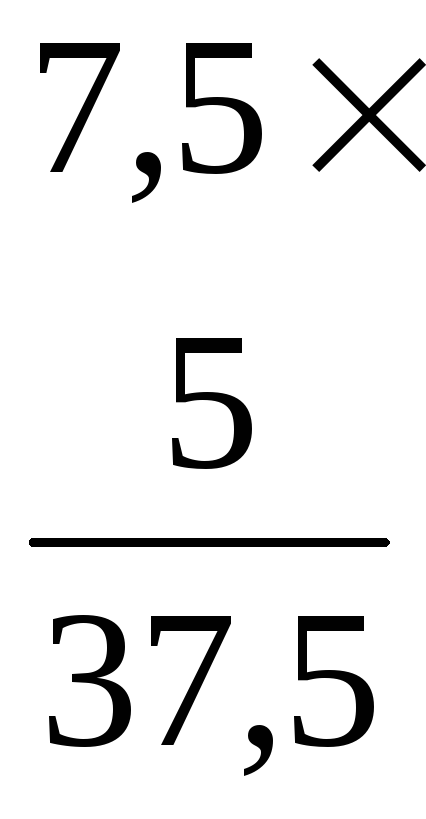
Как и в предыдущем случае, в качестве проверки используем десятичные числа, соответствующие исходным двоичным.

В рассмотренном примере второй разряд множителя равен 0, поэтому второе частичное произведение также равно 0.

1.4. Логические основы работы эвм

Кроме арифметических, ЭВМ выполняют и логические операции, в основе которых положены понятия алгебры логики или, как ее часто называют, булевой алгебры. Основоположником этого раздела математики был Дж. Буль.

Булева алгебра оперирует логическими переменными, которые могут принимать только два значения: истина или ложь, обозначаемые соответственно 1 и 0.

Основной системой счисления ЭВМ является двоичная система счисления, в которой также используются только две цифры: 1 и 0. Таким образом, одни и те же цифровые устройства ЭВМ могут применяться для обработки как числовой информации в двоичной системе счисления, так и логических переменных. Это обуславливает универсальность схемной реализации процесса обработки информации в ЭВМ.

Широкое распространение имеют следующие логические операции: И (логическое умножение), ИЛИ (логическое сложение), НЕ (отрицание). В вычислительной технике они обозначаются соответственно AND (или ) , OR (или ), NOT (или ). С помощью этих трех операций можно представить сколь угодно сложную логическую операцию (логическую функцию). Числа, участвующие в логической операции, называютсяоперандами. Операции И, ИЛИ — двухоперандовые. Операция НЕ — однооперандовая.

Рассмотрим пять основных операций алгебры логики.

1. Операция отрицания. Отрицанием утверждения А называется утверждение, которое ложно, если А истинно, и истинно, если А ложно. Отрицание обозначается (читается «не »). Связь между значением истинности для утверждений и можно выразить с помощью следующей таблицы истинности для отрицания:

1	1	0
2	0	1

Из первой строки таблицы видно, что ложно, если истинно. Вторая строка устанавливает, что истинно, если ложно.

Пример 15. Рассмотрим высказывание

А = {Город Нью-Йорк — столица США}.

Отрицанием этого высказывания будет высказывание

={Город Нью-Йорк не является столицей США}.

Было бы ошибкой считать отрицанием высказывания А высказывание

= {Город Вашингтон — столица США}.

Пример 16. Записать результат выполнения логической операции .

Ответ:

Следует заметить, что результатом логических операций может быть число, отличное от исходных.

2. Операция дизъюнкции.. Дизъюнкцией утверждений A и B называется утверждение, которое истинно, если истинно хотя бы одно из утверждений A и B, и ложно, когда A и B ложны одновременно. Дизъюнкция обозначается символом (читается «A или B») и определяется следующей таблицей истинности:

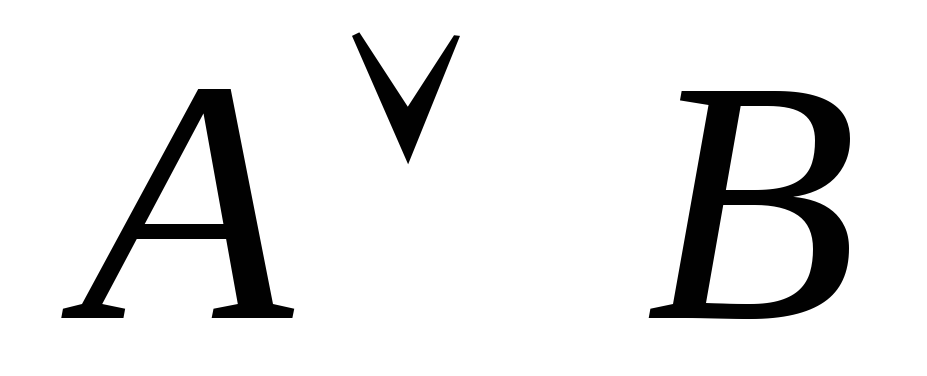
1	1	1	1
2	1	0	1
3	0	1	1
4	0	0	0

Пример 17 . Даны два высказывания

А = {Завтра первый урок литература} и

В= {Завтра первый урок математика}.

Дизъюнкция этих высказываний

= {Завтра первый урок литература или математика}

будет истинной, если на первом уроке будет литература (2-я строка таблицы истинности) или математика (3-я строка таблицы), и ложной, если на первом уроке будет любой другой предмет или если урока вообще не будет (4-я строка таблицы).

Логические действия с двоичными числами выполняются поразрядно. Если количество разрядов в операндах неодинаково, следует дописать незначащие нули.

Пример 18. Логически сложить два двоичных числа 10100010₂ и 1111₂.

Решение:

Ответ: 10100010 1111=10101111

3. Операция конъюнкции. Конъюнкцией утверждений A и B называется утверждение, которое истинно, если истинны оба утверждения A и B, и ложно – в противном случае, т.е. когда хотя бы одно из утверждений ложно. Конъюнкция обозначается символом (читается «A и B») и определяется следующей таблицей истинности:

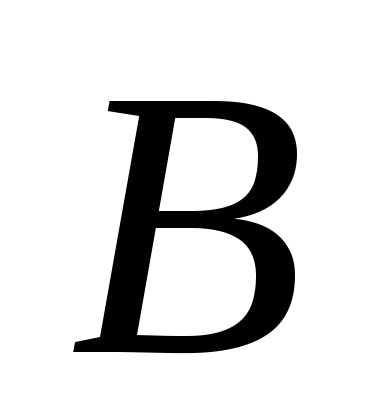
1	1	1	1
2	1	0	0
3	0	1	0
4	0	0	0

Пример 19. Пусть даны высказывания

А = {Петя не любит математику} и

В = {Петя любит физику}.

Конъюнкция = {Петя не любит математику и любит физику} истинна только тогда, когда Петя любит физику, а математику не любит. В остальных трех случаях, т. е. когда Петя:

а) не любит математику и не любит физику,

б) любит математику и физику,

в) любит математику, но не любит физику высказывание ложно.

Для образования конъюнкции в русском языке используются союзы и, а, но, хотя, однако.

Пример 20. Логически перемножить два двоичных числа 11110011₂ и 111111₂.

Решение:

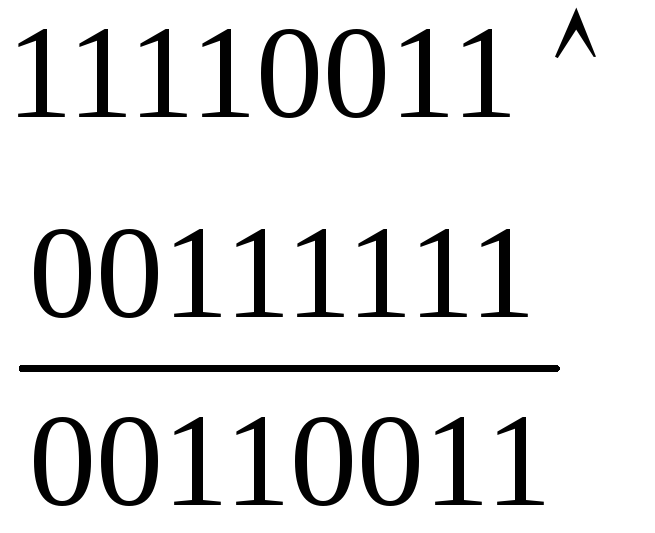
Ответ: 11110011 111111 = 110011

4. Операция эквиваленции. Эквивалентность двух утверждений A и B истинна тогда и только тогда, когда A и B оба истинны или ложны и обозначается А ~ В.

~	A	B	A ~ B
1	1	1	1
2	1	0	0
3	0	1	0
4	0	0	1

Пример 21. Рассмотрим два высказывания

А = {На Марсе будут обнаружены бактерии} и

В = {Сочи станет олимпийской столицей}.

Эквиваленцией этих двух высказываний является высказывание

А ~ В = {На Марсе будут обнаружены бактерии в том и только в том случае, если Сочи станет олимпийской столицей}.

Это высказывание истинно, если:

а) на Марсе будут обнаружены бактерии, и Сочи действительно станет олимпийской столицей;

б) на Марсе не будут обнаружены бактерии, а Сочи не станет олимпийской столицей,

и ложно, если:

в) на Марсе будут найдены бактерии, но олимпийской столицей Сочи не станет;

г) на Марсе не найдут бактерий, а Сочи будет олимпийской столицей.

Для образования эквиваленции используются слова «в том и только в том случае», «тогда и только тогда» и другие.

5. Операция импликации. Импликацией от утверждения А к утверждению В называется утверждение, которое ложно, когда А истинно, а В ложно, и истинно во всех других случаях. Утверждение А называют посылкой, а утверждение B – заключением импликации. Импликация обозначается символом (читается: «из А следует В», « А влечет В», «если А, то В»,) и определяемое следующей таблицей истинности:

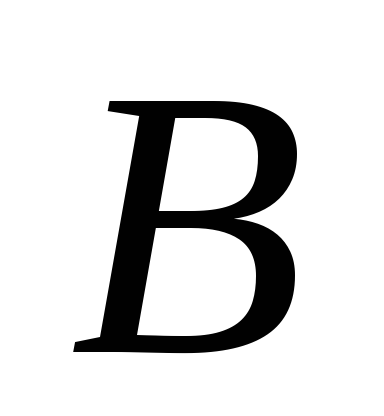
1	1	1	1
2	1	0	0
3	0	1	1
4	0	0	1

Пример 22.

Даны два ложных высказывания

A = {Число 3 является делителем числа 17} и

B = {Число 6 – простое число}.

Высказывание ={Если число 3 – делитель 17, то 6 – простое число} истинно (согласно строке 4 таблицы истинности для импликации).

Введенные пять логических операций дают возможность, исходя из первоначального набора элементарных высказываний, построить некоторое количество сложных высказываний.

Но таблицы истинности на самом деле определяют логические операции не только над элементарными высказываниями, но и над сложными высказываниями. Таким образом, появляется возможность применять логические операции многократно, получая с их помощью все более сложные высказывания. При этом возникает одно затруднение: при записи сложных высказываний может оказаться неясным порядок, в котором следует проводить операции. Это затруднение устраняется введением скобок, которые и устанавливают порядок выполнения операций: операция, заключенная в скобки, выполняется первой.

Истинность или ложность сложного высказывания в зависимости от истинности или ложности составляющих его высказываний можно установить, построив таблицу истинности логических операций.

Пример 22 . Составить таблицу истинности для высказывания

Истина и ложь могут распределяться между двумя высказываниями четырьмя различными способами.

A	B
1	1	1	0	0	1	1
1	0	0	1	0	0	1
0	1	1	0	1	1	1
0	0	1	1	1	1	1

Заполнив таблицу истинности, мы получили важный результат: высказывание ~ истинно всегда, т.е. при любом наборе значений истинны и лжи для составляющих его высказываний A и B. Такие высказывания называются тождественно- истинными и обозначаются латинской буквой I. Поэтому можно записать:

~ = I.

Наряду с тождественно-истинными высказываниями существуют высказывания тождественно-ложные, т.е. ложные всегда, независимо от того, истинны или ложны составляющие их высказывания. Тождественно-ложные высказывания обозначают латинской буквой L.

Формулы, имеющие одинаковые таблицы истинности, назовем эквивалентными. Эквивалентные формулы алгебры высказываний – аналог тождественных выражений обычной алгебры. Так как таблицы истинности конечны, то эквивалентность формул в алгебре высказываний можно доказать с помощью их таблиц истинности, сравнив их. Этот метод практически приемлем только в случае небольшого числа простых высказываний, образующих составные. Ведь если сложное высказывание состоит из n простых, то таблица истинности такого высказывания содержит строк, что приn = 10, например, превзойдет тысячу. В то же время в приложениях алгебры логики, в частности в теории автоматического управления при анализе релейно-контактных и электронно-ламповых схем, как раз приходится иметь дело с высказываниями, составленными из сотен и даже тысяч простых высказываний. Доказательство равносильности высказываний с помощью таблиц истинности в таких случаях практически невозможно.

Равносильность высказываний можно устанавливать и другим способом: некоторое количество основных равносильностей проверяется на основании таблиц истинности, полученные равенства используются при доказательстве других равенств с помощью основных тождеств алгебры высказываний.

Наиболее важными «тождествами» алгебры высказываний являются следующие:

1. Закон двойного отрицания

2. Коммутативность дизъюнкции

3. Коммутативность конъюнкции

4. Ассоциативность дизъюнкции

5. Ассоциативность конъюнкции

6. Первый дистрибутивный закон

7. Второй дистрибутивный закон

8. Законы де Моргана

,

9. Законы идемпотентности

, .

10. Законы, включающие тождественно-истинные (I) и тождественно-ложные (L) высказывания

,

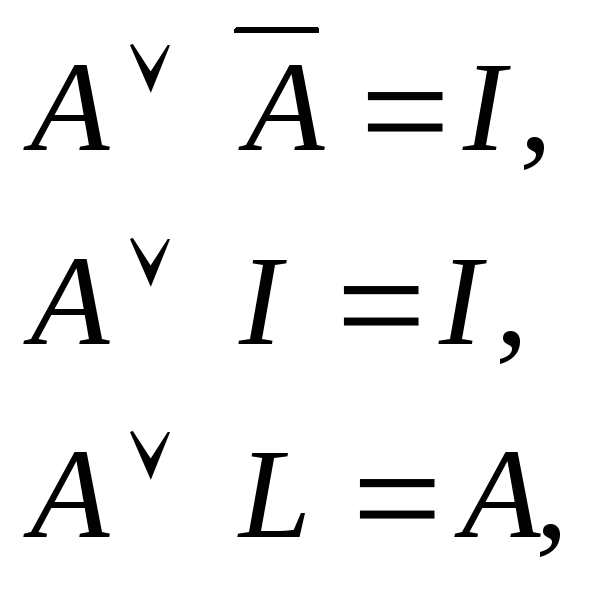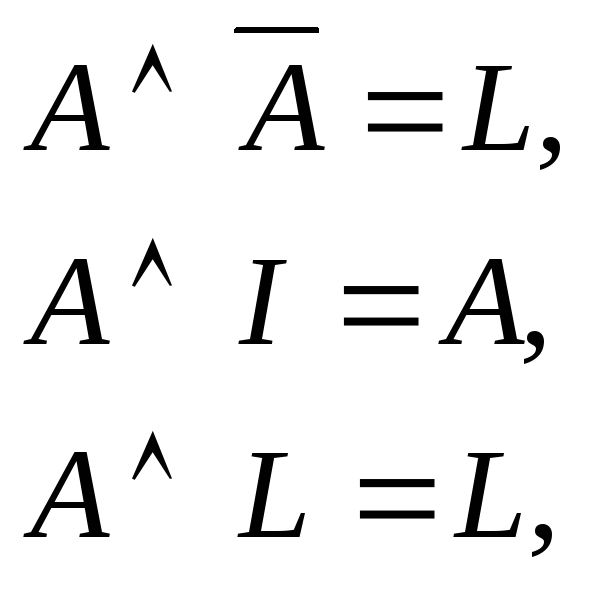
Введенные пять основных логических операций не являются независимыми: одни из них могут быть выражены через другие. В частности, эквиваленция и импликация выражаются через дизъюнкцию, конъюнкцию и отрицание следующим образом:

Пример 23. Доказать равносильность

Используя законы де Моргана, можем записать

Согласно закону двойного отрицания, получаем

теперь, используя первый дистрибутивный закон, преобразуем полученное выражение далее

Ассоциативность дизъюнкции позволяет опустить две пары скобок

учитывая законы пункта 10: иокончательно получаем

Пример 24. Упростить высказывание

Так как

,, ,

то предложенное высказывание равносильно высказыванию , т.е. является тождественно-ложным.

Задача 1.

Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники были на синем «Бьюике»; Джонс сказал, что это был черный «Крайслер», а Смит утверждал, что это был «Форд Мустанг» и ни в коем случае не синий. Стало известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо только ее цвет. Какого цвета был автомобиль, и какой марки?

Решение.

Рассмотрим высказывания:

A = {Машина синего цвета},

B = {Машина марки «Бьюик»},

C = {Машина черного цвета},

D = {Машина марки «Крайслер»},

E = {Машина марки «Форд Мустанг»}.

Так как либо цвет машины, либо марка каждым из соучастников преступления названы верно, то

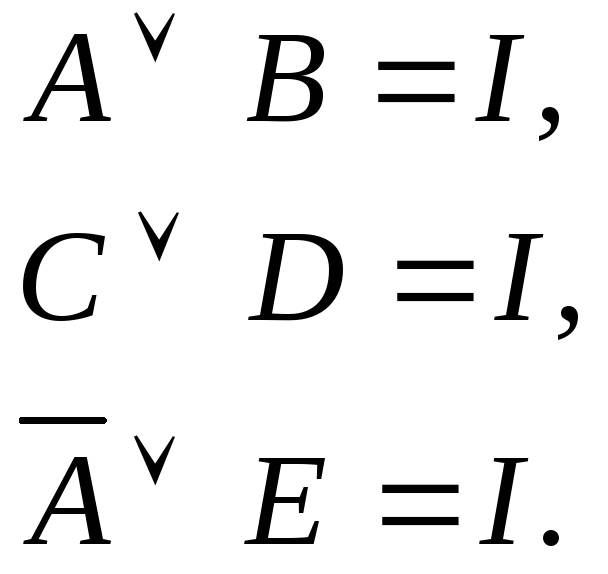
Отсюда следует, что

В левой части конъюнкцию трех дизъюнкций можно, используя первый дистрибутивный закон, заменить дизъюнкцией восьми конъюнкций

Но

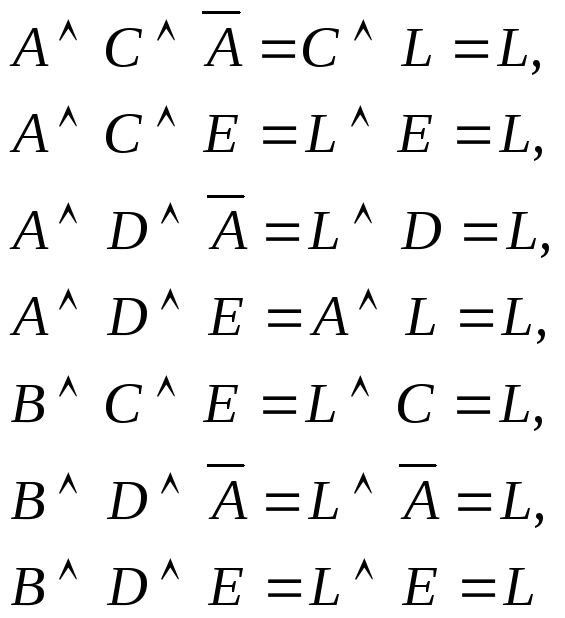
и, следовательно,

, т.е. преступники скрылись на черном «Бьюике».

Задача 2.

На одном заводе работают три друга: слесарь, токарь и плотник. Их фамилии: Борисов, Иванов, Семенов. Профессии и фамилии названы в произвольном порядке. У слесаря нет ни братьев, ни сестер, и он самый младший из друзей. Семенов женат на сестре Борисова, он старше токаря. Назовите фамилии слесаря, токаря и плотника.

Решение.

Составим таблицу, сверху которой для краткости начальными буквами обозначим фамилии друзей и слева – их профессии. В каждую клетку впишем 1, если соответствующая комбинация допустима, или 0, если комбинация противоречит условию задачи.

	Б	И	С
с	0	1	0
т	1	0	0
п	0	0	1

Условия 1 и 3 очевидно исключают возможность того, что Борисов слесарь, поэтому в клетку, стоящую в левом верхнем углу таблицы (клетку (с, Б)), вписываем 0.

Условия 2 и 4 исключают возможность того, что Семенов – слесарь. Поэтому в клетку, стоящую в правом верхнем углу таблицы (клетку (с, С)), также вписываем 0. Но так как один из трех друзей слесарь, то им может быть только Иванов. Поэтому в клетку (с, И) вписываем 1, а в остальные клетки среднего столбца – 0 (если Иванов слесарь, то он не токарь и не плотник).

Условие 4 исключает возможность того, что Семенов токарь. Поэтому в клетку (т, С) вписываем 0, но тогда Семенов может быть только плотником, следовательно, в клетку (п, С) вписываем 1, а в клетку (п, Б) вписываем 0.

Теперь осталась лишь одна незаполненная клетка (т, Б), в которую мы должны, очевидно, вписать 1.

Итак, Борисов – токарь, Иванов – слесарь, Семенов – плотник.

Алгебра логики успешно применяется при анализе релейно-контактных и электронно-ламповых схем. Физическая природа таких схем (будем называть их переключательными) может быть самой разнообразной. Под переключательной системой будем понимать схематическое изображение какого-либо устройства, содержащего только двухпозиционные переключатели, т.е. переключатели, которые могут находиться только в двух состояниях: в замкнутом (ток проходит) и в разомкнутом (ток не проходит). Связь между переключательными схемами и алгеброй высказываний устанавливается следующим образом. Каждому переключателю ставится в соответствие высказывание, истинное тогда, когда переключатель замкнут, и ложное, если переключатель разомкнут. На схемах переключатели будем обозначать теми же буквами, что и соответствующие им высказывания.

Переключателям, соединенным параллельно, будет соответствовать при этом дизъюнкция соответствующих высказываний; переключателям, соединенным последовательно, − конъюнкция высказываний. Если два переключателя работают так, что один из них замкнут, когда другой разомкнут, и наоборот, то им ставятся в соответствие высказывания и.

Каждой переключательной схеме, таким образом, будет поставлено в соответствие сложное высказывание, истинное тогда и только тогда, когда схема проводит ток. Это сложное высказывание можно исследовать методами математической логики. Если такое сложное высказывание удается упростить, то соответствующая схема допускает аналогичное упрощение. Естественно считать из двух схем более простой ту, которая содержит меньше переключателей.

Пример 25. Упростить схему:

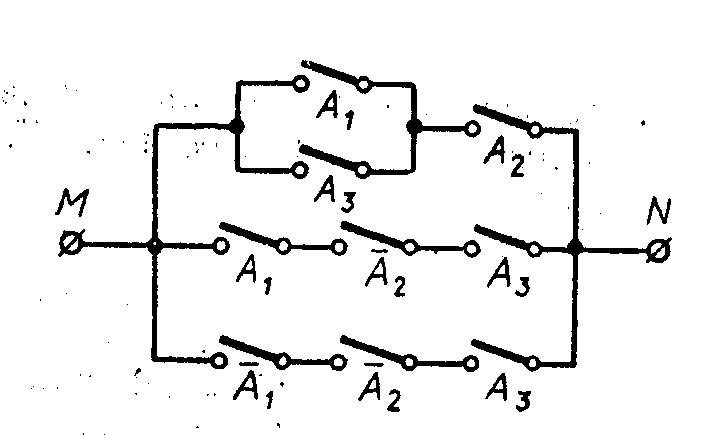
Выписываем высказывание, соответствующее данной схеме, и упрощаем его:

=

==

==

= =.

Следовательно, рассматриваемая схема может быть заменена более простой, содержащей только три переключателя. Исходная схема содержала 9 переключателей. Построим упрощенную схему по аналогии с предыдущей:

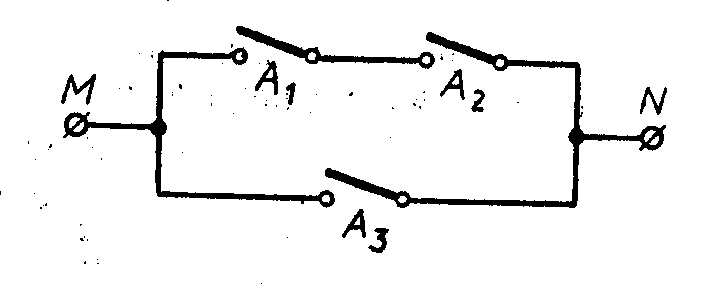
1.5. Содержание отчета:

1. Выполнение заданий соответствующего варианта.

2. Ответы на контрольные вопросы.

1.6. Контрольные вопросы:

1. Что такое система счисления?

2. Чем отличаются позиционная и непозиционная системы счисления?

3. Почему основной системой счисления ЭВМ является двоичная?

4. Когда используется шестнадцатеричная система счисления?

5. Какие основные операции алгебры логики вы знаете?

6. Как можно проверить эквивалентность формул в алгебре высказываний?

16