
- •CONTENTS
- •PREFACE
- •LIST OF FIGURES
- •INTRODUCTION
- •1.1 WHAT IS TIME?
- •1.2 SIMULATION
- •1.3 TESTING
- •1.4 VERIFICATION
- •1.6 USEFUL RESOURCES
- •2.1 SYMBOLIC LOGIC
- •2.1.1 Propositional Logic
- •2.1.2 Predicate Logic
- •2.2 AUTOMATA AND LANGUAGES
- •2.2.1 Languages and Their Representations
- •2.2.2 Finite Automata
- •2.3 HISTORICAL PERSPECTIVE AND RELATED WORK
- •2.4 SUMMARY
- •EXERCISES
- •3.1 DETERMINING COMPUTATION TIME
- •3.2 UNIPROCESSOR SCHEDULING
- •3.2.1 Scheduling Preemptable and Independent Tasks
- •3.2.2 Scheduling Nonpreemptable Tasks
- •3.2.3 Nonpreemptable Tasks with Precedence Constraints
- •3.2.5 Periodic Tasks with Critical Sections: Kernelized Monitor Model
- •3.3 MULTIPROCESSOR SCHEDULING
- •3.3.1 Schedule Representations
- •3.3.3 Scheduling Periodic Tasks
- •3.4 AVAILABLE SCHEDULING TOOLS
- •3.4.2 PerfoRMAx
- •3.4.3 TimeWiz
- •3.6 HISTORICAL PERSPECTIVE AND RELATED WORK
- •3.7 SUMMARY
- •EXERCISES
- •4.1 SYSTEM SPECIFICATION
- •4.2.1 Analysis Complexity
- •4.3 EXTENSIONS TO CTL
- •4.4 APPLICATIONS
- •4.4.1 Analysis Example
- •4.5 COMPLETE CTL MODEL CHECKER IN C
- •4.6 SYMBOLIC MODEL CHECKING
- •4.6.1 Binary Decision Diagrams
- •4.6.2 Symbolic Model Checker
- •4.7.1 Minimum and Maximum Delays
- •4.7.2 Minimum and Maximum Number of Condition Occurrences
- •4.8 AVAILABLE TOOLS
- •4.9 HISTORICAL PERSPECTIVE AND RELATED WORK
- •4.10 SUMMARY
- •EXERCISES
- •VISUAL FORMALISM, STATECHARTS, AND STATEMATE
- •5.1 STATECHARTS
- •5.1.1 Basic Statecharts Features
- •5.1.2 Semantics
- •5.4 STATEMATE
- •5.4.1 Forms Language
- •5.4.2 Information Retrieval and Documentation
- •5.4.3 Code Executions and Analysis
- •5.5 AVAILABLE TOOLS
- •5.6 HISTORICAL PERSPECTIVE AND RELATED WORK
- •5.7 SUMMARY
- •EXERCISES
- •6.1 SPECIFICATION AND SAFETY ASSERTIONS
- •6.4 RESTRICTED RTL FORMULAS
- •6.4.1 Graph Construction
- •6.5 CHECKING FOR UNSATISFIABILITY
- •6.6 EFFICIENT UNSATISFIABILITY CHECK
- •6.6.1 Analysis Complexity and Optimization
- •6.7.2 Timing Properties
- •6.7.3 Timing and Safety Analysis Using RTL
- •6.7.5 RTL Representation Converted to Presburger Arithmetic
- •6.7.6 Constraint Graph Analysis
- •6.8 MODECHART SPECIFICATION LANGUAGE
- •6.8.1 Modes
- •6.8.2 Transitions
- •6.9.1 System Computations
- •6.9.2 Computation Graph
- •6.9.3 Timing Properties
- •6.9.4 Minimum and Maximum Distance Between Endpoints
- •6.9.5 Exclusion and Inclusion of Endpoint and Interval
- •6.10 AVAILABLE TOOLS
- •6.11 HISTORICAL PERSPECTIVE AND RELATED WORK
- •6.12 SUMMARY
- •EXERCISES
- •7.1.1 Timed Executions
- •7.1.2 Timed Traces
- •7.1.3 Composition of Timed Automata
- •7.1.4 MMT Automata
- •7.1.6 Proving Time Bounds with Simulations
- •7.2.1 Untimed Traces
- •7.2.2 Timed Traces
- •7.3.1 Clock Regions
- •7.3.2 Region Automaton
- •7.4 AVAILABLE TOOLS
- •7.5 HISTORICAL PERSPECTIVE AND RELATED WORK
- •7.6 SUMMARY
- •EXERCISES
- •TIMED PETRI NETS
- •8.1 UNTIMED PETRI NETS
- •8.2 PETRI NETS WITH TIME EXTENSIONS
- •8.2.1 Timed Petri Nets
- •8.2.2 Time Petri Nets
- •8.3 TIME ER NETS
- •8.3.1 Strong and Weak Time Models
- •8.5.1 Determining Fireability of Transitions from Classes
- •8.5.2 Deriving Reachable Classes
- •8.6 MILANO GROUP’S APPROACH TO HLTPN ANALYSIS
- •8.6.1 Facilitating Analysis with TRIO
- •8.7 PRACTICALITY: AVAILABLE TOOLS
- •8.8 HISTORICAL PERSPECTIVE AND RELATED WORK
- •8.9 SUMMARY
- •EXERCISES
- •PROCESS ALGEBRA
- •9.1 UNTIMED PROCESS ALGEBRAS
- •9.2 MILNER’S CALCULUS OF COMMUNICATING SYSTEMS
- •9.2.1 Direct Equivalence of Behavior Programs
- •9.2.2 Congruence of Behavior Programs
- •9.2.3 Equivalence Relations: Bisimulation
- •9.3 TIMED PROCESS ALGEBRAS
- •9.4 ALGEBRA OF COMMUNICATING SHARED RESOURCES
- •9.4.1 Syntax of ACSR
- •9.4.2 Semantics of ACSR: Operational Rules
- •9.4.3 Example Airport Radar System
- •9.5 ANALYSIS AND VERIFICATION
- •9.5.1 Analysis Example
- •9.5.2 Using VERSA
- •9.5.3 Practicality
- •9.6 RELATIONSHIPS TO OTHER APPROACHES
- •9.7 AVAILABLE TOOLS
- •9.8 HISTORICAL PERSPECTIVE AND RELATED WORK
- •9.9 SUMMARY
- •EXERCISES
- •10.3.1 The Declaration Section
- •10.3.2 The CONST Declaration
- •10.3.3 The VAR Declaration
- •10.3.4 The INPUTVAR Declaration
- •10.3.5 The Initialization Section INIT and INPUT
- •10.3.6 The RULES Section
- •10.3.7 The Output Section
- •10.5.1 Analysis Example
- •10.6 THE ANALYSIS PROBLEM
- •10.6.1 Finite Domains
- •10.6.2 Special Form: Compatible Assignment to Constants,
- •10.6.3 The General Analysis Strategy
- •10.8 THE SYNTHESIS PROBLEM
- •10.8.1 Time Complexity of Scheduling Equational
- •10.8.2 The Method of Lagrange Multipliers for Solving the
- •10.9 SPECIFYING TERMINATION CONDITIONS IN ESTELLA
- •10.9.1 Overview of the Analysis Methodology
- •10.9.2 Facility for Specifying Behavioral Constraint Assertions
- •10.10 TWO INDUSTRIAL EXAMPLES
- •10.10.2 Specifying Assertions for Analyzing the FCE Expert System
- •Meta Rules of the Fuel Cell Expert System
- •10.11.1 General Analysis Algorithm
- •10.11.2 Selecting Independent Rule Sets
- •10.11.3 Checking Compatibility Conditions
- •10.12 QUANTITATIVE TIMING ANALYSIS ALGORITHMS
- •10.12.1 Overview
- •10.12.2 The Equational Logic Language
- •10.12.3 Mutual Exclusiveness and Compatibility
- •10.12.5 Program Execution and Response Time
- •10.12.8 Special Form A and Algorithm A
- •10.12.9 Special Form A
- •10.12.10 Special Form D and Algorithm D
- •10.12.11 The General Analysis Algorithm
- •10.12.12 Proofs
- •10.13 HISTORICAL PERSPECTIVE AND RELATED WORK
- •10.14 SUMMARY
- •EXERCISES
- •11.1 THE OPS5 LANGUAGE
- •11.1.1 Overview
- •11.1.2 The Rete Network
- •11.2.1 Static Analysis of Control Paths in OPS5
- •11.2.2 Termination Analysis
- •11.2.3 Timing Analysis
- •11.2.4 Static Analysis
- •11.2.5 WM Generation
- •11.2.6 Implementation and Experiment
- •11.3.1 Introduction
- •11.3.3 Response Time of OPS5 Systems
- •11.3.4 List of Symbols
- •11.3.5 Experimental Results
- •11.3.6 Removing Cycles with the Help of the Programmer
- •11.4 HISTORICAL PERSPECTIVE AND RELATED WORK
- •11.5 SUMMARY
- •EXERCISES
- •12.1 INTRODUCTION
- •12.2 BACKGROUND
- •12.3 BASIC DEFINITIONS
- •12.3.1 EQL Program
- •12.3.4 Derivation of Fixed Points
- •12.4 OPTIMIZATION ALGORITHM
- •12.5 EXPERIMENTAL EVALUATION
- •12.6 COMMENTS ON OPTIMIZATION METHODS
- •12.6.1 Qualitative Comparison of Optimization Methods
- •12.7 HISTORICAL PERSPECTIVE AND RELATED WORK
- •12.8 SUMMARY
- •EXERCISES
- •BIBLIOGRAPHY
- •INDEX
BASIC DEFINITIONS |
439 |
approach in the worst case requires exponential computation time as a function of the number of variables in the program [Browne, Cheng, and Mok, 1988].
We have implemented the methods on a class of real-time decision systems where decisions are computed by an equational rule-based (EQL) program. Corresponding analysis tools were developed to estimate the time responses for programs written in other production languages, for example, MRL [Wang and Mok, 1993] and OPS5 [Chen and Cheng, 1995a].
Within the deductive database research, similar concepts are presented by [Abiteboul and Simon, 1991]. They discuss the totalness and loop-freeness of a deductive system, which, in the terminology of rule-based systems, describes the stability of the systems in terms of the initial points reaching their fixed points in finite time.
If the analysis finds that the given real-time rule-based program meets the integrity but not the timing constraints, the program has to be optimized. We define this as the synthesis problem, which has to determine whether an extension of the original real-time system exists that would meet both timing and integrity constraints. The solution may be achieved by either (1) transforming the given equational rule-based program or (2) optimizing the scheduler to select the rules to fire such that some fixed point is always reached within the response-time constraint. The latter assumes that there is at least one sufficiently short path from a launch state to every one of its end points. In chapter 10, we gave an example for both solutions, but did not propose a corresponding algorithm.
In our definition of the synthesis problem, the original program is supposed to satisfy the integrity constraints. To obtain the optimized program satisfying the same constraints, we require that each launch state of the optimized program has the same set of corresponding fixed points as the original program. We believe that the optimization can benefit highly by easing this constraint, so that for each launch state the optimized program would have only a single corresponding fixed point taken from the set of fixed points of the unoptimized system. Such system has a deterministic behavior. [Aiken, Widom, and Hellerstein, 1992] formalize this concept for database production rules and discuss the observable determinism of a rule set. The rule set is observably deterministic if the execution order does not make any difference in the order of appearance of the observable actions. Similar concepts can be found in the process-algebraic approach described in chapter 9.
The chapter is organized as follows. We first review the necessary background and discuss in more detail the analysis and synthesis problem of real-time rule-based systems. Next we review the EQL rule-based language, its execution model and its state-space representation. Several optimization algorithms are then presented. We next experimentally evaluate these optimization algorithms. The methods—their limitations and possible extensions—are finally discussed.
12.3 BASIC DEFINITIONS
The real-time programs considered here belong to the class of EQL programs. Here we define the syntax of EQL programs and its execution model, define the measure
440 OPTIMIZATION OF RULE-BASED SYSTEMS
for the response time of the EQL system, and formally introduce their state-space graphs.
12.3.1 EQL Program
An EQL program is given in the form of n rules (r1, . . . , rn ) that operate over the set of m variables (x1, . . . , xm ). Each rule has action and condition parts. Formally,
Fk (s) IF ECk (s)
where k {1, . . . , n}, ECk (s) is an enabling condition of rule k, and Fk (s) is an action. Both the enabling condition and the action are defined over the state s of a system. Each state s is expressed as a tuple, s = (x1, . . . , xm ), where xi represents a value of ith variable. An action Fk is given as a series of nk ≥ 1 subactions separated by “!”:
Fk ≡ Lk,1 := Rk,1(x1, . . . , xm ) ! . . . !
Lk,nk := Rk,nk (x1, . . . , xm )
The subactions are interpreted from left to right. Each subaction sets the value of variable Lk,i {x1, . . . , xm } to the value returned by the function Rk,i , i {1, . . . , nk }. The enabling condition ECk (s) is a two-valued function that evaluates to TRUE for the states where rules can fire.
Throughout the chapter we will use two-valued variables only, that is, xi {0, 1}. We will identify this subset of EQL by EQL(B). Any EQL program with a predefined set of possible values of the variables can be converted into the EQL(B). Due to the simplicity of such conversion, here we show only an example. Consider the following rules:
i := 2 IF j < 2 AND i = 3
[] j := i IF i = 2
where i and j are four-valued variables with their values i, j {0, 1, 2, 3}. The corresponding EQL(B) rules using two-valued variables i1, i2, j1, and j2 are:
i0 |
:= TRUE |
! i1 := FALSE |
|
|||
|
IF (NOT |
j0 |
AND NOT j1) |
OR |
||
|
|
(NOT |
j0 |
AND |
j1) AND |
(i0 AND i1) |
[] j0 |
:= |
i0 ! |
j1 |
:= i1 |
|
|
|
IF |
(i0 AND |
NOT |
i1) |
|
|
Furthermore, we constrain EQL(B) to use only constant assignments in the subactions of rules, that is, Ri, j {0, 1}. This can potentially reduce the complexity of optimization algorithms (see Section 12.3.4).
An example of an EQL(B) program is given in Figure 12.1. This program will be used in the following sections to demonstrate the various effects of the optimization. For clarity, the example program is intentionally kept simple. In practice, our method can be used for the systems of much higher complexity, possibly consisting of several hundred rules.

|
|
|
BASIC DEFINITIONS |
441 |
|
|
|
||
PROGRAM an_eql_b_program; |
|
|
||
VAR |
|
|
|
|
a, b, c, d : BOOLEAN; |
|
|
||
RULES |
|
|
|
|
(* 1 *) |
c:=1 IF a=0 |
AND b=0 AND d=0 |
|
|
(* 2 *) [] |
b:=1 IF d=0 |
AND (a=1 OR c=1) |
|
|
(* 3 *) [] |
a:=1 ! c:=1 |
IF a=0 AND d=0 AND (b=1 OR c=1) |
|
|
(* 4 |
*) [] |
b:=0 ! c:=0 |
IF d=0 AND b=1 AND |
|
|
|
|
(a=0 AND c=1 OR a=1 AND c=0) |
|
(* 5 |
*) [] |
d:=0 ! a:=1 |
IF a=1 AND c=1 AND d=1 |
|
END. |
|
|
|
|
Figure 12.1 An example of the EQL(B) rule-based expert system.
12.3.2Execution Model of a Real-Time Decision System Based on an EQL Program Paradigm
Real-time decision systems based on the EQL program paradigm interact with the environment through sensor readings. Readings are then represented as the values of variables used in the EQL program that implements the decision system. The variables derived directly from sensor readings are called input variables. All other variables are called system variables. After the input variables are set the EQL program is invoked. Repeatedly, among the enabled rules a conflict resolution strategy is used to select a rule to fire. This (possibly) changes the state of the system, and
sensor |
|
|
Environment |
|
|
|
decision |
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
monitor |
|
|
|||
readings |
|
|
|
|
vector |
||
|
|
cycle |
|
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
yes |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Fixed |
||
|
|
|
|
|
|||
|
|
|
Rule Based EQL |
|
|||
|
|
|
|
Point |
|||
|
|
|
|||||
|
|
|
Decision System |
|
|||
|
|
|
|
Reached? |
|||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
decide |
no |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
cycle |
|
|
|
|
|
|
|
|
|
|
||
|
|
EQL program variables |
|
|
|
||
Figure 12.2 An EQL program-based decision system.

442 OPTIMIZATION OF RULE-BASED SYSTEMS
the whole process of firing is repeated until either no more rules are enabled or rule firing does not change the system’s state. The resulting state is called a fixed point. The values of the variables are then communicated back to the environment.
The process of reading the sensor variables, invoking the EQL program, and communicating back the values of the fixed point is called the monitor cycle. A fixed point is determined in a repetitive EQL invocation named the decide cycle (Figure 12.2).
As described in chapter 10, EQL’s response time is the time an EQL system spends to reach a fixed point, or, equivalently, the time spent in the decide cycle. A real-time decision system is said to satisfy the timing constraints if the response time is smaller or equal to the smallest time interval between two sensor readings. A response time can be assessed by a maximum number of rules to be fired to reach a fixed point. The conversion from number of rule firings to response time can be done if one knows the time spent for identification of a rule to fire and the time spent for firing the rule itself. These times depend on the specific architecture of an implementation and will not be discussed here.
12.3.3 State-Space Representation
In order to develop an optimization method, we view an EQL(B) system as a transition system T , which is a triple, (S, R, →), where
1.S is a finite set of states. Assuming a finite set V of two-valued variables x1, x2, . . . , xm and an ordering of V, S is the set of all 2m possible Cartesian products of the values of variables;
2.R is a set of rules r1, r2, . . . , rn in the system’s rule base;
3.→ is a mapping associated with each rk R, that is, a transition relation
→rk S × S. If rk is enabled at s1 S and firing of rk at that state s1 results in
rk |
, or shorter, s1 |
k |
the new state s2 S, we can write s1 → s2 |
→ s2. |
A graphical representation of a transition system T is a labeled finite directed transition or state-space graph G = (V, E). V is a set of vertices, each labeled with the states s S. E is a set of edges labeled with rk R. An edge rk connects vertex s1 to s2 if and only if s1 →rk s2. A path in a transition graph is a sequence of vertices such that for each consecutive pair si , s j in a sequence, there exists a rule rk R
such that si →rk s j . If a path exists from si to s j , s j is said to be reachable from si . A cycle is a path from a vertex to itself.
A state-space graph for the program from Figure 12.1 is shown in Figure 12.3. Throughout the chapter we use the following labeling scheme: edges are labeled with the rule responsible for the transition, and vertices are labeled with the two-valued expression, which evaluates to TRUE for a state represented by a vertex. After the introduction of the equivalent states (section 12.4.2), we will also allow the vertices to be labeled with a two-valued expression denoting a set of states and allow edges to be labeled with a set of rules. We use a compact notation for two-valued expressions. For example, ab represents a conjunction of a and b, a+b denotes a disjunction of a and b, and a represents a negation of a.
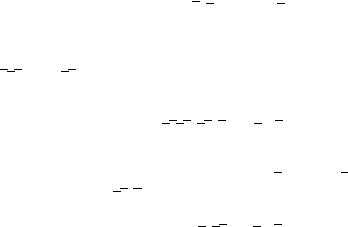
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BASIC DEFINITIONS |
443 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
abcd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
r4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
abcd |
|
|
|
|
|
|
|
|
|
|
abcd |
|
abcd |
|
abcd |
|
||||||||||||||||||||||||
|
|
|
|
r3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r3 |
|
|
|
|
|
|
|
|
r4 |
|
|
|
|
|
|
|
|
r2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
r5 |
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
abcd |
|
|
abcd |
r5 |
|
abcd |
|
|
|
|
|
|
|
|
|
|
abcd |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
abcd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
abcd |
|
abcd |
|
abcd |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
abcd |
|
abcd |
|
|
|
|
abcd |
|
||||||||||||||||
Figure 12.3 State-space graph for the EQL(B) program in Figure 12.1.
Each state may belong to one or more categories of states, which are:
•fixed point: A state is said to be a fixed-point state if it does not have any outedges or if all of the out-edges are self-loops. For the state-space graph in Figure 12.3, an example of fixed points are abcd, abcd, and abcd.
•unstable: A state is unstable if no fixed point is reachable from it. Because such states have to have out-edges (or else it would be a fixed point state), it either has to be involved in a cycle or has to have reachable a state involved in a cycle. States abcd and abcd from Figure 12.3 are unstable.
•potentially unstable: A potentially unstable state is either an unstable state or a state with a reachable fixed point, and either is involved in a cycle or has a path to the state involved in a cycle. States abcd, abcd, and abcd from Figure 12.3 are potentially unstable.
•stable: A stable state is either a fixed point or a state from which no unstable or potentially unstable state is reachable. For example, states abcd and abcd from Figure 12.3 are stable, while abcd is not.
•potentially stable: A potentially stable state is one with a reachable fixed point or is a fixed point itself. For example, states abcd and abcd from Figure 12.3 are potentially stable.
•launch: The state in which the program is invoked is called the launch state.
Stable states are a subset of potentially stable states. Unstable states are a subset of potentially unstable states. No unstable state is potentially stable. Any valid state is either potentially stable or unstable.
