
- •CONTENTS
- •PREFACE
- •LIST OF FIGURES
- •INTRODUCTION
- •1.1 WHAT IS TIME?
- •1.2 SIMULATION
- •1.3 TESTING
- •1.4 VERIFICATION
- •1.6 USEFUL RESOURCES
- •2.1 SYMBOLIC LOGIC
- •2.1.1 Propositional Logic
- •2.1.2 Predicate Logic
- •2.2 AUTOMATA AND LANGUAGES
- •2.2.1 Languages and Their Representations
- •2.2.2 Finite Automata
- •2.3 HISTORICAL PERSPECTIVE AND RELATED WORK
- •2.4 SUMMARY
- •EXERCISES
- •3.1 DETERMINING COMPUTATION TIME
- •3.2 UNIPROCESSOR SCHEDULING
- •3.2.1 Scheduling Preemptable and Independent Tasks
- •3.2.2 Scheduling Nonpreemptable Tasks
- •3.2.3 Nonpreemptable Tasks with Precedence Constraints
- •3.2.5 Periodic Tasks with Critical Sections: Kernelized Monitor Model
- •3.3 MULTIPROCESSOR SCHEDULING
- •3.3.1 Schedule Representations
- •3.3.3 Scheduling Periodic Tasks
- •3.4 AVAILABLE SCHEDULING TOOLS
- •3.4.2 PerfoRMAx
- •3.4.3 TimeWiz
- •3.6 HISTORICAL PERSPECTIVE AND RELATED WORK
- •3.7 SUMMARY
- •EXERCISES
- •4.1 SYSTEM SPECIFICATION
- •4.2.1 Analysis Complexity
- •4.3 EXTENSIONS TO CTL
- •4.4 APPLICATIONS
- •4.4.1 Analysis Example
- •4.5 COMPLETE CTL MODEL CHECKER IN C
- •4.6 SYMBOLIC MODEL CHECKING
- •4.6.1 Binary Decision Diagrams
- •4.6.2 Symbolic Model Checker
- •4.7.1 Minimum and Maximum Delays
- •4.7.2 Minimum and Maximum Number of Condition Occurrences
- •4.8 AVAILABLE TOOLS
- •4.9 HISTORICAL PERSPECTIVE AND RELATED WORK
- •4.10 SUMMARY
- •EXERCISES
- •VISUAL FORMALISM, STATECHARTS, AND STATEMATE
- •5.1 STATECHARTS
- •5.1.1 Basic Statecharts Features
- •5.1.2 Semantics
- •5.4 STATEMATE
- •5.4.1 Forms Language
- •5.4.2 Information Retrieval and Documentation
- •5.4.3 Code Executions and Analysis
- •5.5 AVAILABLE TOOLS
- •5.6 HISTORICAL PERSPECTIVE AND RELATED WORK
- •5.7 SUMMARY
- •EXERCISES
- •6.1 SPECIFICATION AND SAFETY ASSERTIONS
- •6.4 RESTRICTED RTL FORMULAS
- •6.4.1 Graph Construction
- •6.5 CHECKING FOR UNSATISFIABILITY
- •6.6 EFFICIENT UNSATISFIABILITY CHECK
- •6.6.1 Analysis Complexity and Optimization
- •6.7.2 Timing Properties
- •6.7.3 Timing and Safety Analysis Using RTL
- •6.7.5 RTL Representation Converted to Presburger Arithmetic
- •6.7.6 Constraint Graph Analysis
- •6.8 MODECHART SPECIFICATION LANGUAGE
- •6.8.1 Modes
- •6.8.2 Transitions
- •6.9.1 System Computations
- •6.9.2 Computation Graph
- •6.9.3 Timing Properties
- •6.9.4 Minimum and Maximum Distance Between Endpoints
- •6.9.5 Exclusion and Inclusion of Endpoint and Interval
- •6.10 AVAILABLE TOOLS
- •6.11 HISTORICAL PERSPECTIVE AND RELATED WORK
- •6.12 SUMMARY
- •EXERCISES
- •7.1.1 Timed Executions
- •7.1.2 Timed Traces
- •7.1.3 Composition of Timed Automata
- •7.1.4 MMT Automata
- •7.1.6 Proving Time Bounds with Simulations
- •7.2.1 Untimed Traces
- •7.2.2 Timed Traces
- •7.3.1 Clock Regions
- •7.3.2 Region Automaton
- •7.4 AVAILABLE TOOLS
- •7.5 HISTORICAL PERSPECTIVE AND RELATED WORK
- •7.6 SUMMARY
- •EXERCISES
- •TIMED PETRI NETS
- •8.1 UNTIMED PETRI NETS
- •8.2 PETRI NETS WITH TIME EXTENSIONS
- •8.2.1 Timed Petri Nets
- •8.2.2 Time Petri Nets
- •8.3 TIME ER NETS
- •8.3.1 Strong and Weak Time Models
- •8.5.1 Determining Fireability of Transitions from Classes
- •8.5.2 Deriving Reachable Classes
- •8.6 MILANO GROUP’S APPROACH TO HLTPN ANALYSIS
- •8.6.1 Facilitating Analysis with TRIO
- •8.7 PRACTICALITY: AVAILABLE TOOLS
- •8.8 HISTORICAL PERSPECTIVE AND RELATED WORK
- •8.9 SUMMARY
- •EXERCISES
- •PROCESS ALGEBRA
- •9.1 UNTIMED PROCESS ALGEBRAS
- •9.2 MILNER’S CALCULUS OF COMMUNICATING SYSTEMS
- •9.2.1 Direct Equivalence of Behavior Programs
- •9.2.2 Congruence of Behavior Programs
- •9.2.3 Equivalence Relations: Bisimulation
- •9.3 TIMED PROCESS ALGEBRAS
- •9.4 ALGEBRA OF COMMUNICATING SHARED RESOURCES
- •9.4.1 Syntax of ACSR
- •9.4.2 Semantics of ACSR: Operational Rules
- •9.4.3 Example Airport Radar System
- •9.5 ANALYSIS AND VERIFICATION
- •9.5.1 Analysis Example
- •9.5.2 Using VERSA
- •9.5.3 Practicality
- •9.6 RELATIONSHIPS TO OTHER APPROACHES
- •9.7 AVAILABLE TOOLS
- •9.8 HISTORICAL PERSPECTIVE AND RELATED WORK
- •9.9 SUMMARY
- •EXERCISES
- •10.3.1 The Declaration Section
- •10.3.2 The CONST Declaration
- •10.3.3 The VAR Declaration
- •10.3.4 The INPUTVAR Declaration
- •10.3.5 The Initialization Section INIT and INPUT
- •10.3.6 The RULES Section
- •10.3.7 The Output Section
- •10.5.1 Analysis Example
- •10.6 THE ANALYSIS PROBLEM
- •10.6.1 Finite Domains
- •10.6.2 Special Form: Compatible Assignment to Constants,
- •10.6.3 The General Analysis Strategy
- •10.8 THE SYNTHESIS PROBLEM
- •10.8.1 Time Complexity of Scheduling Equational
- •10.8.2 The Method of Lagrange Multipliers for Solving the
- •10.9 SPECIFYING TERMINATION CONDITIONS IN ESTELLA
- •10.9.1 Overview of the Analysis Methodology
- •10.9.2 Facility for Specifying Behavioral Constraint Assertions
- •10.10 TWO INDUSTRIAL EXAMPLES
- •10.10.2 Specifying Assertions for Analyzing the FCE Expert System
- •Meta Rules of the Fuel Cell Expert System
- •10.11.1 General Analysis Algorithm
- •10.11.2 Selecting Independent Rule Sets
- •10.11.3 Checking Compatibility Conditions
- •10.12 QUANTITATIVE TIMING ANALYSIS ALGORITHMS
- •10.12.1 Overview
- •10.12.2 The Equational Logic Language
- •10.12.3 Mutual Exclusiveness and Compatibility
- •10.12.5 Program Execution and Response Time
- •10.12.8 Special Form A and Algorithm A
- •10.12.9 Special Form A
- •10.12.10 Special Form D and Algorithm D
- •10.12.11 The General Analysis Algorithm
- •10.12.12 Proofs
- •10.13 HISTORICAL PERSPECTIVE AND RELATED WORK
- •10.14 SUMMARY
- •EXERCISES
- •11.1 THE OPS5 LANGUAGE
- •11.1.1 Overview
- •11.1.2 The Rete Network
- •11.2.1 Static Analysis of Control Paths in OPS5
- •11.2.2 Termination Analysis
- •11.2.3 Timing Analysis
- •11.2.4 Static Analysis
- •11.2.5 WM Generation
- •11.2.6 Implementation and Experiment
- •11.3.1 Introduction
- •11.3.3 Response Time of OPS5 Systems
- •11.3.4 List of Symbols
- •11.3.5 Experimental Results
- •11.3.6 Removing Cycles with the Help of the Programmer
- •11.4 HISTORICAL PERSPECTIVE AND RELATED WORK
- •11.5 SUMMARY
- •EXERCISES
- •12.1 INTRODUCTION
- •12.2 BACKGROUND
- •12.3 BASIC DEFINITIONS
- •12.3.1 EQL Program
- •12.3.4 Derivation of Fixed Points
- •12.4 OPTIMIZATION ALGORITHM
- •12.5 EXPERIMENTAL EVALUATION
- •12.6 COMMENTS ON OPTIMIZATION METHODS
- •12.6.1 Qualitative Comparison of Optimization Methods
- •12.7 HISTORICAL PERSPECTIVE AND RELATED WORK
- •12.8 SUMMARY
- •EXERCISES
- •BIBLIOGRAPHY
- •INDEX

344 DESIGN AND ANALYSIS OF PROPOSITIONAL-LOGIC RULE-BASED SYSTEMS
5 |
G1 |
G2 |
1 |
4
2
G3 |
|
3 |
|
6 |
|
|
G4 |
|
|
|
|
|
|
7 |
Figure 10.14 The ME graph of Program 2.
Example 10. The following is a sample Special Form A program.
PROGRAM Program 2 VAR
c, d, e, f, g, h : integer; x, y, z : boolean;
INPUTVAR
a, b : integer ; INIT
c:= 0, d := 0, e := 0, f := 0, g := 0, h := 0, x := true, y := true, z := true
INPUT read(a, b)
RULES
(*1*) c := 1 IF a > 0 and b > 0 (*2*) [] c := 2 IF a > 0 and b ≤ 0 (*3*) [] c := 3 IF a ≤ 0 and b > 0
(*4*) [] c := 4 IF a ≤ 0 and b ≤ 0
(*5*) [] e := 1 | f := 1 IF a ≤ 0 or b ≤ 0 (*6*) [] d := 1 | f := 1 IF a ≤ 0 or b > 0 (*7*) [] d := 1 | e := 1 IF a > 0 or b > 0
END.
Applying Algorithm A to Program 2, step 1 constructs the ME graph GProgramM E 2 that can be divided into four subgraphs in step 2: G1 contains four vertices (rules),
G2, G3, and G4 each contains only one vertex, as shown in Figure 10.14. Hence, step 3 determines that there are at most four rule firings during the execution of Program 2.
10.12.10 Special Form D and Algorithm D
Special Form D is a relaxed version of Special Form A since it allows variables in L p to appear in Tp and Rp, where p is a Special Form D program. For each rule
QUANTITATIVE TIMING ANALYSIS ALGORITHMS |
345 |
r in p, r may be dynamically enabled and disabled throughout the execution of p. This means that r may be fired more than once before p reaches a fixed point. On the other hand, the fact that r is enabled does not necessarily mean that r will be fired before p reaches a fixed point. It may be the case that the firings of other rules disable r before r gets an opportunity to be fired.
Rule-Dependency Graph The firing of r may result in the firing of r , if (1) r potentially enables r or (2) Lr ∩ Rr = . Each of these two conditions represents one potential firing sequence consisting of the firing of r followed by the firing of r . The former results from the dependency between the LHS of r and the EC of r , whereas the latter results from the dependency between the LHS of r and the RHS of r . The rule-dependency graphs are used to demonstrate potential firing sequences of EQL programs.
Rule-Dependency Graph: Let S denote a set of rules. The rule-dependency (RD) graph G SR D = (V, M, N ) is a labeled directed graph. V is a set of vertices representing subrules such that V contains a vertex labeled ri if and only if there is a subrule ri in S. M is a set of directed edges, called ER edges, such that M contains the edgeri , r j if and only if ri potentially enables r j . N is a set of directed edges, called VM edges, such that N contains the edge ri , r j if and only if
1.Lri ∩ Rr j = , and
2.ri does not disable r j if ri and r j do not mutually exclude each other, or ri
if ri and r j mutually exclude each other.
A cycle C in G SR D is classified as
•an ER cycle if it contains only ER edges, or
•a VM cycle if it contains only VM edges, or
•an EV cycle if it contains both kinds of edges.
It is possible that a variable xi (Lri ∩ Tr j ) exists such that it cannot be decided textually whether the value assigned to xi by ri is in Vr j ,xi . If this is the case, we assume the value assigned to xi is in Vr j ,xi , thus indicating that the ER edge ri , r j
exists from the vertex ri to the vertex r j in the actual implementation of the RD graph. In addition, in the worst case, the construction procedure requires exponential time as a function of the number of subrules to construct the RD graph, due to the checks for the property of mutual exclusiveness and enabledness/disabledness.
Note that although the existence of the ER edge ri , r j in G SR D does not necessarily mean that the subrule r j will be enabled as a result of the firing of the subrule ri , it does mean that r j may be enabled (and hence fired) as a result of the firing of ri . On the other hand, if the VM edge ri , r j exists in G SR D , then ri assigns a value
346 DESIGN AND ANALYSIS OF PROPOSITIONAL-LOGIC RULE-BASED SYSTEMS
to a variable x Rr j such that the value of the RHS of r j may change as a result of the firing of ri . Hence, the firing of ri may result in the firing of r j , too. If there
|
|
j |
|
|
S |
is a path ri , r |
, . . . , wk , bm , dl |
|
in G R D , then the firing of ri may eventually result |
||
the firing of d |
|
|
|
||
inR D |
|
l . In addition, if there is a cycle C = ri , u j , . . . , wk , bm , dl , ri in |
|||
G S |
, then the subrules in C may be repeatedly fired one after another an unlimited |
||||
number of times such that S does not reach a fixed point in any bounded time. |
|||||
Now, let ri |
and r j |
be two subrules in S of the form |
|||
x = f1(y) IF E1
and
y = f2(x) IF E2,
respectively. G SR D contains a VM cycle C consisting of only ri and r j . The equality assertion x == f1(y) must be true immediately after the firing of ri , and the equality assertion y == f2(x) must be true immediately after the firing of r j . If these two equality assertions can be rewritten in such a way that they are identical, then there can be at most one subrule firing among ri and r j if no other subrule is fired. For example, assume f1(y) = y + 1 and f2(x) = x − 1. The firing of either subrule, say ri , prevents the other, r j , from being fired, since the firing of r j immediately after the firing of ri does not change the value of a variable. Therefore, it is not possible for ri and r j to be alternately fired for an unlimited number of times such that S does not reach a fixed point in bounded time. If this is the case, then C is called a convergent cycle. Note that a convergent cycle is a VM cycle consisting of only two subrules (vertices), belonging to two different rules.
Special Form D The first condition of Special Form D ensures that each pair of rules cannot alternately change the value of a variable for an unlimited number of time, while the other conditions ensure that rules cannot be cyclically fired.
Special Form D: Let S denote a set of rules. S is in Special Form D if the following conditions hold.
D1. For each pair of distinct rules r and r in S, r and r are compatible.
D2. |
The rule-dependency graph G R D does not contain an EV cycle. |
|
||||||||
|
S |
|
|
|
|
|
|
|
|
|
D3. |
For each ER cycle in G SR D , there does not exist a pair of subrules ri and r j |
|||||||||
|
|
|
|
|
|
|
|
(Lri |
∩ |
j |
|
that disagree on the expression assigned to a variable x |
|
|
Lr ). |
||||||
D4. |
There does not exist a pair of subrules ri |
C1 |
and r j |
C2, where C1 and |
||||||
|
C2 are distinct simple ER cycles in G SR D , such that ri and r j disagree on the |
|||||||||
|
expression assigned to a variable x |
|
(Lri |
∩ |
Lr |
j |
|
|
|
|
|
|
|
). |
|
|
|
|
|||
D5. For each simple VM cycle C in G SR D , C is a convergent cycle, or the subrules (vertices) contained in C cannot all be enabled at the same time (i.e.,
∩r C Vr = ).

QUANTITATIVE TIMING ANALYSIS ALGORITHMS |
347 |
To check if a set of rules is in Special Form D, the recognition procedure requires exponential time in the worst case since it requires exponential time to determine all directed cycles in a directed graph [Garey and Johnson, 1979]. However, the RD graph is usually sparse, so the time required to check the satisfaction of Special Form D conditions is just a small fraction of what is required to conduct the state-space graph check.
Assume p is a Special Form D program. By the definition of Special Form D, p does not contain a rule that includes an assignment expression of the form x := f (x); otherwise, a one-vertex VM cycle C in G Rp D would exist, violating (D5) since C contains only one vertex. Also, a cycle C in G Rp D does not exist such that all of the subrules (vertices) in C belong to the same rule in p. If such a C did exist, (D5) would be violated since all of these subrules would have the same enabling condition.
Theorem 6. If p is in Special Form D, then the execution of p always terminates in a bounded number of rule firings.
Proof of Theorem 6. The proof can be found in section 10.12.12.
Algorithm D Assume p is an n-rule Special Form D program. To find an upper bound on the number of rule firings during the execution of p, the Divide-and- Conquer strategy is employed here. For each rule r p, r can be fireable (and hence fired) because (1) the launch state makes r fireable or (2) the firings of other rules make r fireable. According to the definition of program execution, the execution of p is a sequence of rule firings. From the view point of counting the number of rule firings, this sequence of rule firings can be regarded as being composed of interleaving subsequences, each of which starts with the firing of some rule which is fireable at the launch state (i.e., we say this rule initiates a subsequence of rule firings during the execution of p). Note that it is possible that a rule can initiate a subsequence of rule firings and be initiated by the firing(s) of other rules during the same execution.
Since there are n rules in p, at most n subsequences of rule firings exist during the execution of p. The number of rule firings during the execution of p is equal to the sum of the numbers of rule firings in individual subsequences. According to Theorem 6, the execution of p always terminates in a bounded number of rule firings. This means that each subsequence consists of up to a bounded number of rule firings, and hence there is a finite upper bound on the number of rule firings in each subsequence. Let N Ir denote an upper bound on the number of rule firings in the subsequence initiated by r. The sum of N Ir s, one for each rule r p, is thus an upper bound on the number of rule firings during the execution of p. That is,
|
|
T p = N Ir |
(10.2) |
r p
To obtain N Ir , the divide-and-conquer strategy is employed again. Since each subrule may have an influence on other rules and hence result in the firings of other rules, directly or indirectly, each subrule ri of r may initiate a sub-subsequence of
348 DESIGN AND ANALYSIS OF PROPOSITIONAL-LOGIC RULE-BASED SYSTEMS
rule firings. Let N Iri denote an upper bound on the number of rule firings in the subsubsequence initiated by the firing of ri . The sum of N Iri s, one for each subrule ri of r, is thus an upper bound on the number of rule firings in the subsequence initiated by the firing of r. That is,
|
|
N Ir = N Iri |
(10.3) |
ri r
By the definition of rule firing and subrule firing, the sum of the numbers of times that the subrules of the rule g are fired (as a result of the firing of ri ) is not less than
the number of times that g is fired (as a result of the firing of ri ). An upper bound |
||||||||
on the former is thus also an upper bound on the latter. Let N I g j denote an upper |
||||||||
bound on the number of times that g j |
|
|
|
|
ri |
|||
is fired as a result of the firing of ri . The sum |
||||||||
of N I g j |
s, one for each subrule g |
j |
of g, is an upper bound on the number of times |
|||||
ri |
|
|
|
. Let N I g |
|
|
||
that g is fired as a result of the firing of r |
denote this upper bound. The |
|||||||
|
|
|
|
i |
|
ri |
|
|
sum of all N Irgi s, one for each rule g p, is thus an upper bound on the number of |
||||||||
rule firings in the sub-subsequence initiated by the firings of ri . That is, |
||||||||
|
N Iri |
= |
N Irgi |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
g p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
N Irgi j |
|
(10.4) |
|
|
|
|
|
g j p |
|
|
|
|
|
|
|
|
i denote a |
|
|
N I g j . From now on, to sim- |
|
We now show how to compute the value of |
g j p |
|||||||
plify the notations used, for all i, let r |
|
subrule of some rule of p. Further- |
||||||
more, ri |
and r j do not have to be subrules of the same rule. As mentioned earlier, if |
|||||||
the edge r1, r2 in G Rp D exists, the firing of r1 may result in the firing of r2 since r1 either assigns a new value to a variable in Rr2 (thus changes the RHS value of r2) or potentially enables r2. If there is a path r1, r2, . . . , rk in G Rp D , the firing of r1 may eventually result in the firing of rk . Hence, any vertex (subrule) in G Rp D reachable by r1 can possibly be fired as a result of the firing of r1 (i.e., it can possibly be in the sub-subsequence initiated by the firing of r1). Furthermore, if more than one path from the vertex r1 to the vertex rk in G Rp D exist, rk may be fired more than once due to the firing of r1, and the number of paths between r1 and rk is the number of possible firings of rk as a result of the firing of r1. That is due to the fact that rk may
be invoked by r1 along each of these paths.
Now, assume C = r1, r2, . . . , rk−1, rk , r1 is a cycle in G Rp D . Since G Rp D does not contain an EV cycle (i.e., (D2)), C must be either an ER cycle or a VM cycle.
•C is an ER cycle. For each i, 1 ≤ i ≤ k − 1, ri+1 may be enabled due to the firing of ri . It is possible that, starting with r1, the subrules in C are fired one after another in order of their positions in C. Due to (D3), none of the
variables in C is assigned distinct values by distinct subrules in C. Hence, after a sequence of firings along the path r1, r2, . . . , rk , the variable in Lr1 will not be assigned a new value by a second firing of r1 since it is not assigned a distinct

QUANTITATIVE TIMING ANALYSIS ALGORITHMS |
349 |
value by other subrules in C. This means the firing of r1 cannot cause another firing of r1.
•C is a VM cycle. Along the path of C, for each i, 1 ≤ i ≤ k − 1, ri+1 may be fireable due to the fact that the firing of ri changes the value of the variable in
Rri+1 . However, due to (D5), C contains at least one subrule, say r j , which is disabled when r1 is enabled. In addition, r j cannot be enabled as a result of the firing of any subrule in C; otherwise, an EV cycle would exist, violating (D2). Hence, the firing of r1 cannot result in the firing of r j along the path of C. This also means the firing of r1 cannot cause another firing of r1.
Furthermore, assume there is a subrule ri of the form x := f If EC such that ri potentially enables r j and x Rr j . Not only does an ER edge ri , r j exist, but also a VM edge ri , r j exists in G Rp D . However, the effect of the firing of ri on r j via these two edges happens simultaneously. These two edges together should be treated as a single edge in terms of potential firing sequence. Hence, we first transform the RD graph into a simplified RD (SRD) graph, GSRDp , by combining edges connecting the same pair of vertices into one edge.
Based on the fact described above, we use a variation of the standard Depth- First-Search algorithm given in [Aho, Hopcroft, and Ullman, 1974] to traverse the simplified RD graph and obtain the maximal number of subrule firings as a result of the firing of the source vertex. Figure 10.15 outlines this modified algorithm.
Assume ri is the source vertex. A global variable, counter, initialized to 0, is used to record the number of times that vertices are visited, representing the number of possible subrule firings as a result of the firing of ri . This algorithm starts the process of search from ri . Each time a vertex is visited, a new path from ri to this vertex has been found. In general, suppose x is the most recently visited vertex. The search continues by selecting some unexplored edge x, v . If v is not an “ancestor” of x, then v will be visited next, the variable counter will be increased by 1, and a new search starting from v will begin; otherwise, another unexplored out-going edge from
Procedure DFS(v);
Begin
counter := counter + 1;
For each edge v, w GSRDp Do
If w is not an ancestor of v, then
Begin
DFS(w);
End;
End ;
Figure 10.15 Modified depth-first-search algorithm.

350 DESIGN AND ANALYSIS OF PROPOSITIONAL-LOGIC RULE-BASED SYSTEMS
x will be selected. This process continues until all of the out-going edges from x are explored. When the traversal is finished, the value of counter stands for the maximal number of possible subrule (and thus rule) firings as a result of the firing of ri (i.e.,
N Iri = counter).
Once we obtain all of the N Iri s of the subrules in p, we can obtain an upper bound on the number of rule firings during the execution of p by applying equations (10.2) and (10.3). However, we can tighten this upper bound by exploiting the property of mutual exclusiveness among rules, as we do in the case of Algorithm A.
If a rule is disabled at the launch state of an execution, it cannot initiate a subsequence of rule firings during this particular execution. If r and r are compatible by the property of mutual exclusiveness, then at least one of them, say r, is disabled at the launch state. This means that r cannot initiate a subsequence of rule firings during the execution of p. Hence, N Ir should not be counted in computing the upper bound for p. If a set of m rules exists in which each pair of distinct rules is compatible by the property of mutual exclusiveness, the argument above applies to each pair of rules in this set (i.e., at most one rule in this set can possibly initiate a subsequence of rule firings). This means that only one of the N Ir s corresponding to the rules in this set should be counted.
Hence, for the purpose of obtaining a tighter upper bound, the ME graph is partitioned into a minimal number of independent complete subgraphs such that the least number of N Ir s needs to be counted. Assume k is the minimal number of independent complete subgraphs of GMEp and pi is the set of rules corresponding to the ith independent complete ME subgraph. For each pi , 1 ≤ i ≤ k, there is at most one rule that can initiate a subsequence of rule firings during the execution of p. Although we do not know in advance which rule in pi can initiate a subsequence of rule firings, we do know that the number of rule firings initiated by that rule cannot be greater
than maxr pi (N Ir ). Hence, we obtain the following upper bound for p: |
|
||||||||||
|
|
|
|
T p |
= |
max(N I ). |
(10.5) |
||||
|
|
|
|
|
|
r |
|
pi |
r |
|
|
|
|
|
|
|
|
|
pi ,1≤i≤k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Input |
A Special Form D program p. |
|
|
|
|
|
|||||
Output An integer representing an upper bound for p. |
|
|
|||||||||
1. |
For each subrule ri GSRDp |
, apply depth-first-search algorithm to ri to obtain N Iri . |
|||||||||
2. |
For each rule r, obtain N Ir |
= |
ri |
N Iri . |
|
|
|
|
|||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Partition GME into a minimal number, k, of independent complete subgraphs. |
|
|||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
4. |
Output( |
|
max(N I )). |
|
|
|
|
|
|
||
r pi |
r |
|
|
|
|
|
|
|
|||
Figure 10.16 Algorithm D.
QUANTITATIVE TIMING ANALYSIS ALGORITHMS |
351 |
Figure 10.16 shows the resulting algorithm by applying the strategies described above. Step 1 requires O( i mi )-time in the worst case, where each mi is the number of edges in the ith layer during the depth-first search. From our experience, the SRD graph is usually sparse and thus the value of mi is usually small. Step 2 and step 4 require linear time to perform the summation and output operations. Step 3 requires quadratic time, as in the case of Algorithm A.
Example 11. The following is a sample Special Form D program.
PROGRAM Program 3 VAR
w, x, y, z, t, v : integer; INPUTVAR
g, h, i : integer;
INIT
w := 1, x := 1, y := 1, z := 1, t := 1, v := 1 INPUT
read(g, h, i)
RULES
(*1*) x := 1 | w := y IF g = 0 and y = 1 (*2*) [] x := 0 | w := y IF g = 1
(*3*) [] y := 1 | t := x IF h = 0 and x = 1 (*4*) [] z := 2 t IF t > 0
(*5*) [] v := 0 IF x = 0 and i = 0 (*6*) [] v := 1 IF x = 0 and i = 1 (*7*) [] v := 1 IF x = 1 and i = 1
END.
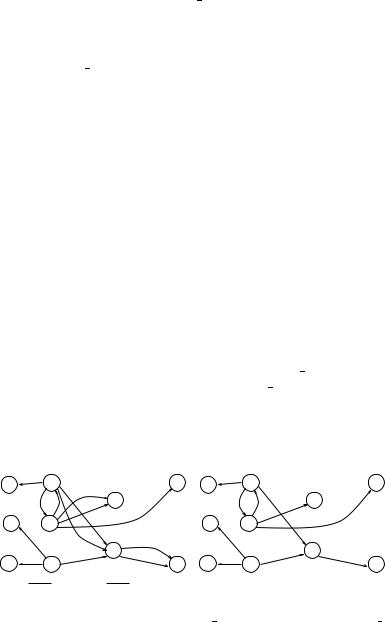
The RD graph and the simplified RD graph of Program 3 are shown in Figures 10.17(a) and (b), respectively. Applying Algorithm D, for each subrule ri , step 1 finds all of the possible firing sequences starting from the firing of ri . Figure 10.18 shows the subrules that are reachable by the subrule 11 (and hence can possibly be fired as a result of the firing of 11). That is, step 1 determines that N I11 = 7. Simi-
7 1 |
1 1 |
2 2 |
7 1 |
1 1 |
2 2 |
|
1 2 |
|
|
|
1 2 |
6 1 |
3 1 |
|
6 1 |
3 1 |
|
|
3 2 |
|
|
|
3 2 |
5 1 |
2 1 |
4 1 |
5 1 |
2 1 |
4 1 |
|
VM edge |
ER edge |
|
|
|
|
(a) |
|
|
|
(b) |
Figure 10.17 (a) The RD graph of Program 3. (b) The SRD graph of Program 3.
