
- •CONTENTS
- •PREFACE
- •LIST OF FIGURES
- •INTRODUCTION
- •1.1 WHAT IS TIME?
- •1.2 SIMULATION
- •1.3 TESTING
- •1.4 VERIFICATION
- •1.6 USEFUL RESOURCES
- •2.1 SYMBOLIC LOGIC
- •2.1.1 Propositional Logic
- •2.1.2 Predicate Logic
- •2.2 AUTOMATA AND LANGUAGES
- •2.2.1 Languages and Their Representations
- •2.2.2 Finite Automata
- •2.3 HISTORICAL PERSPECTIVE AND RELATED WORK
- •2.4 SUMMARY
- •EXERCISES
- •3.1 DETERMINING COMPUTATION TIME
- •3.2 UNIPROCESSOR SCHEDULING
- •3.2.1 Scheduling Preemptable and Independent Tasks
- •3.2.2 Scheduling Nonpreemptable Tasks
- •3.2.3 Nonpreemptable Tasks with Precedence Constraints
- •3.2.5 Periodic Tasks with Critical Sections: Kernelized Monitor Model
- •3.3 MULTIPROCESSOR SCHEDULING
- •3.3.1 Schedule Representations
- •3.3.3 Scheduling Periodic Tasks
- •3.4 AVAILABLE SCHEDULING TOOLS
- •3.4.2 PerfoRMAx
- •3.4.3 TimeWiz
- •3.6 HISTORICAL PERSPECTIVE AND RELATED WORK
- •3.7 SUMMARY
- •EXERCISES
- •4.1 SYSTEM SPECIFICATION
- •4.2.1 Analysis Complexity
- •4.3 EXTENSIONS TO CTL
- •4.4 APPLICATIONS
- •4.4.1 Analysis Example
- •4.5 COMPLETE CTL MODEL CHECKER IN C
- •4.6 SYMBOLIC MODEL CHECKING
- •4.6.1 Binary Decision Diagrams
- •4.6.2 Symbolic Model Checker
- •4.7.1 Minimum and Maximum Delays
- •4.7.2 Minimum and Maximum Number of Condition Occurrences
- •4.8 AVAILABLE TOOLS
- •4.9 HISTORICAL PERSPECTIVE AND RELATED WORK
- •4.10 SUMMARY
- •EXERCISES
- •VISUAL FORMALISM, STATECHARTS, AND STATEMATE
- •5.1 STATECHARTS
- •5.1.1 Basic Statecharts Features
- •5.1.2 Semantics
- •5.4 STATEMATE
- •5.4.1 Forms Language
- •5.4.2 Information Retrieval and Documentation
- •5.4.3 Code Executions and Analysis
- •5.5 AVAILABLE TOOLS
- •5.6 HISTORICAL PERSPECTIVE AND RELATED WORK
- •5.7 SUMMARY
- •EXERCISES
- •6.1 SPECIFICATION AND SAFETY ASSERTIONS
- •6.4 RESTRICTED RTL FORMULAS
- •6.4.1 Graph Construction
- •6.5 CHECKING FOR UNSATISFIABILITY
- •6.6 EFFICIENT UNSATISFIABILITY CHECK
- •6.6.1 Analysis Complexity and Optimization
- •6.7.2 Timing Properties
- •6.7.3 Timing and Safety Analysis Using RTL
- •6.7.5 RTL Representation Converted to Presburger Arithmetic
- •6.7.6 Constraint Graph Analysis
- •6.8 MODECHART SPECIFICATION LANGUAGE
- •6.8.1 Modes
- •6.8.2 Transitions
- •6.9.1 System Computations
- •6.9.2 Computation Graph
- •6.9.3 Timing Properties
- •6.9.4 Minimum and Maximum Distance Between Endpoints
- •6.9.5 Exclusion and Inclusion of Endpoint and Interval
- •6.10 AVAILABLE TOOLS
- •6.11 HISTORICAL PERSPECTIVE AND RELATED WORK
- •6.12 SUMMARY
- •EXERCISES
- •7.1.1 Timed Executions
- •7.1.2 Timed Traces
- •7.1.3 Composition of Timed Automata
- •7.1.4 MMT Automata
- •7.1.6 Proving Time Bounds with Simulations
- •7.2.1 Untimed Traces
- •7.2.2 Timed Traces
- •7.3.1 Clock Regions
- •7.3.2 Region Automaton
- •7.4 AVAILABLE TOOLS
- •7.5 HISTORICAL PERSPECTIVE AND RELATED WORK
- •7.6 SUMMARY
- •EXERCISES
- •TIMED PETRI NETS
- •8.1 UNTIMED PETRI NETS
- •8.2 PETRI NETS WITH TIME EXTENSIONS
- •8.2.1 Timed Petri Nets
- •8.2.2 Time Petri Nets
- •8.3 TIME ER NETS
- •8.3.1 Strong and Weak Time Models
- •8.5.1 Determining Fireability of Transitions from Classes
- •8.5.2 Deriving Reachable Classes
- •8.6 MILANO GROUP’S APPROACH TO HLTPN ANALYSIS
- •8.6.1 Facilitating Analysis with TRIO
- •8.7 PRACTICALITY: AVAILABLE TOOLS
- •8.8 HISTORICAL PERSPECTIVE AND RELATED WORK
- •8.9 SUMMARY
- •EXERCISES
- •PROCESS ALGEBRA
- •9.1 UNTIMED PROCESS ALGEBRAS
- •9.2 MILNER’S CALCULUS OF COMMUNICATING SYSTEMS
- •9.2.1 Direct Equivalence of Behavior Programs
- •9.2.2 Congruence of Behavior Programs
- •9.2.3 Equivalence Relations: Bisimulation
- •9.3 TIMED PROCESS ALGEBRAS
- •9.4 ALGEBRA OF COMMUNICATING SHARED RESOURCES
- •9.4.1 Syntax of ACSR
- •9.4.2 Semantics of ACSR: Operational Rules
- •9.4.3 Example Airport Radar System
- •9.5 ANALYSIS AND VERIFICATION
- •9.5.1 Analysis Example
- •9.5.2 Using VERSA
- •9.5.3 Practicality
- •9.6 RELATIONSHIPS TO OTHER APPROACHES
- •9.7 AVAILABLE TOOLS
- •9.8 HISTORICAL PERSPECTIVE AND RELATED WORK
- •9.9 SUMMARY
- •EXERCISES
- •10.3.1 The Declaration Section
- •10.3.2 The CONST Declaration
- •10.3.3 The VAR Declaration
- •10.3.4 The INPUTVAR Declaration
- •10.3.5 The Initialization Section INIT and INPUT
- •10.3.6 The RULES Section
- •10.3.7 The Output Section
- •10.5.1 Analysis Example
- •10.6 THE ANALYSIS PROBLEM
- •10.6.1 Finite Domains
- •10.6.2 Special Form: Compatible Assignment to Constants,
- •10.6.3 The General Analysis Strategy
- •10.8 THE SYNTHESIS PROBLEM
- •10.8.1 Time Complexity of Scheduling Equational
- •10.8.2 The Method of Lagrange Multipliers for Solving the
- •10.9 SPECIFYING TERMINATION CONDITIONS IN ESTELLA
- •10.9.1 Overview of the Analysis Methodology
- •10.9.2 Facility for Specifying Behavioral Constraint Assertions
- •10.10 TWO INDUSTRIAL EXAMPLES
- •10.10.2 Specifying Assertions for Analyzing the FCE Expert System
- •Meta Rules of the Fuel Cell Expert System
- •10.11.1 General Analysis Algorithm
- •10.11.2 Selecting Independent Rule Sets
- •10.11.3 Checking Compatibility Conditions
- •10.12 QUANTITATIVE TIMING ANALYSIS ALGORITHMS
- •10.12.1 Overview
- •10.12.2 The Equational Logic Language
- •10.12.3 Mutual Exclusiveness and Compatibility
- •10.12.5 Program Execution and Response Time
- •10.12.8 Special Form A and Algorithm A
- •10.12.9 Special Form A
- •10.12.10 Special Form D and Algorithm D
- •10.12.11 The General Analysis Algorithm
- •10.12.12 Proofs
- •10.13 HISTORICAL PERSPECTIVE AND RELATED WORK
- •10.14 SUMMARY
- •EXERCISES
- •11.1 THE OPS5 LANGUAGE
- •11.1.1 Overview
- •11.1.2 The Rete Network
- •11.2.1 Static Analysis of Control Paths in OPS5
- •11.2.2 Termination Analysis
- •11.2.3 Timing Analysis
- •11.2.4 Static Analysis
- •11.2.5 WM Generation
- •11.2.6 Implementation and Experiment
- •11.3.1 Introduction
- •11.3.3 Response Time of OPS5 Systems
- •11.3.4 List of Symbols
- •11.3.5 Experimental Results
- •11.3.6 Removing Cycles with the Help of the Programmer
- •11.4 HISTORICAL PERSPECTIVE AND RELATED WORK
- •11.5 SUMMARY
- •EXERCISES
- •12.1 INTRODUCTION
- •12.2 BACKGROUND
- •12.3 BASIC DEFINITIONS
- •12.3.1 EQL Program
- •12.3.4 Derivation of Fixed Points
- •12.4 OPTIMIZATION ALGORITHM
- •12.5 EXPERIMENTAL EVALUATION
- •12.6 COMMENTS ON OPTIMIZATION METHODS
- •12.6.1 Qualitative Comparison of Optimization Methods
- •12.7 HISTORICAL PERSPECTIVE AND RELATED WORK
- •12.8 SUMMARY
- •EXERCISES
- •BIBLIOGRAPHY
- •INDEX
388 TIMING ANALYSIS OF PREDICATE-LOGIC RULE-BASED SYSTEMS
This cycle contains only the fourth rule. It implies the other rules can terminate in finite firings. The fourth rule is
(p check-group
(device ^mode { <x> <> void } ^domain <y>
^compnt <z1> ^desc { <w> << open closed >> }) (device ^mode <x> ^domain <y> ^compnt <z2> ^desc <w>) (valve_groups ^vtype <v> ^valve_a <z1> ^valve_b <z2>)
-->
(modify 1 ^compnt <v>) (modify 2 ^mode void))
We then examine the non-terminating rule with the enabling condition of the cycle. We find that the program flow can enter the cycle when variable <z1> is equal to variable <z2> in the rule check-group. This situation is not expected as a normal execution flow. Hence, we modify the LHS of this rule such that variable <z1> is not equal to variable <z2>.
(p check-group
(device ^mode { <x> <> void } ^domain <y>
^compnt <z1> ^desc { <w> << open closed >> })
(device ^mode <x> ^domain <y> ^compnt { <z2> <> <z1> } ^desc <w>) (valve_groups ^vtype <v> ^valve_a <z1> ^valve_b <z2>)
-->
(modify 1 ^compnt <v>) (modify 2 ^mode void))
This modification breaks the cycle, thus guaranteeing the termination of this rule and the program. In the next section, we introduce techniques for determining the execution time of OPS5 programs.
11.2.3 Timing Analysis
Now we introduce techniques for analyzing the timing properties of OPS5 programs and discuss a static-analytic method to predict the timing bound on program execution time. The ER graph is the basic structure of our static analysis. We predict the timing in terms of the number of rule firings. Similar work has been done for MRL in [Wang and Mok, 1993]. We will indicate the problems of static analysis and describe a tool to facilitate the timing analysis and to assist programmers in analyzing run-time performance.
Before we analyze the problem, we need to make the following assumptions:
•The program can terminate.
•The data domains of all attributes are finite.
•No duplicate WMEs are in the WM.
The first assumption is obvious since no timing bound can be found for a program with infinite firings. The second assumption is based on the fact that the analysis

CHENG–TSAI TIMING ANALYSIS METHODOLOGY |
389 |
problem is in general undecidable for programs with infinite domains. The third assumption is actually an extension of the second assumption. Unlike MRL, OPS5’s WMEs are identified not only by their contents but also by their time tags. Thus, the following two WMEs are identified as different items in OPS5; the first WME is generated earlier than the second WME. However, identical WMEs cannot co-exist in the WM in MRL.
time tag |
WMEs |
___________________________________
#3 (class ^a1 3 ^a2 4)
#6 (class ^a1 3 ^a2 4)
An OPS5 system can use a hash table to quickly locate the duplicate WMEs in the WM and prevent redundancy in every cycle. If a set of WMEs satisfies the enabling condition of the first firing rule, we can generate the same WMEs as many times as we want. In other words, we can fire the first-firing rule as many times as we want. This indicates that no upper bound exists for this rule’s firings, and thus the program cannot terminate in a finite number of rule firings. Therefore, we need to enforce the third assumption to facilitate our analysis.
11.2.4 Static Analysis
Prediction of the Number of Rule Firings Since the execution of rule-based programs is data-driven, the WM is used to predict the number of rule firings. To predict the number of each rule’s firings, we estimate the number of instantiations in the conflict set. The maximum number of instantiations of a rule can be estimated, as in example 10.
Example 10. An example with a maximum number of instantiations.
(p a
(class_a ^a1 <x> ^a2 <y>) (class_b ^b1 <x> ^b2 <z>) (class_c ^c1 <z>)
-->
action without changing the instantiations of rule a ...
Assume the domains of <x>,<y>, and <z> contain at most x, y, and z instances, respectively. Then, we have at most x yz instantiations of rule a in the conflict set. Suppose the action of rule a does not remove any instantiations of rule a. There are two situations in which rule a can be fired: (1) the initial WM contains rule a’s instantiations, or (2) rule a is triggered by other rules.
In the first situation, we have at most x yz instantiations in the initial WM. Thus rule a can fire at most x yz times before rule a is triggered by other rules.
In the second situation, another rule creates or modifies WME w which matches one or more enabling condition elements of rule a. If the WME w matches the first condition element, (class a ^a1 <x> ^a2 <y>), at most z of rule a instantiations will
390 TIMING ANALYSIS OF PREDICATE-LOGIC RULE-BASED SYSTEMS
be added into the conflict set because variables <x> and <y> are bound with the values of w’s attributes. Thus rule a can fire at most z times before it is again triggered by other rules. Similarly, if w matches (class b ^b1 <x> ^b2 <z>) or (class c ^c1 <z>), rule a can fire at most y or x y times, respectively, before another rule triggers rule a again.
Also, the action part of a rule can affect the rule’s instantiations. For example, the rule in example 10 can be
(p a
(class_a ^a1 <x> ^a2 <y>) (class_b ^b1 <x> ^b2 <z>) (class_c ^c1 <z>)
-->
(modify 3 ^c1 <y>))
Once the value of attribute ^c1 is changed, the instantiations associated with the third condition element, (class c ^c1 <z>), will be removed. Thus the maximum number of firings is the number of instances of <z>, that is, z. Also, we reduce the maximum number of firings from x yz to z. If rule a is triggered with the match of the third condition element, (class c ^c1 <z>), rule a can fire at most once before another trigger.
Algorithm 2. Detection of the upper bound on the number of firings of rule r.
Premise: rule r can be detected to terminate in bounded time by using the termination detection algorithm 1.
Suppose we have up to Ir instantiations of rule r in the initial WM. The upper bound on the firings of rule r can be estimated according to the following conditions.
1.Rule r satisfies condition 1 of theorem 1: the upper bound on the firings of rule r is Ir . The maximum number of the initial WMEs is bounded by the domain size of each attribute.
2.Rule r satisfies condition 2 of theorem 1: rules r1, r2, . . . , rn are enabling rules of the matched condition elements of rule r. These rules can terminate in f1, f2, . . . , fn firings, respectively. Rule r has at most I1, I2, . . . , In instantiations when triggered by r1, r2, . . . , rn . The upper bound on the number of firings of rule r is
n
Ir + ( f j × I j )
j=1
3.Rule r satisfies condition 3 of theorem 1: rules r1, r2, . . . , rm , which point to rule r in the ER graph can terminate in f1, f2, . . . , fm firings, respectively. Rule r has at most I1, I2, . . . , Im instantiations when triggered by
CHENG–TSAI TIMING ANALYSIS METHODOLOGY |
391 |
r1, r2, . . . , rm . The upper bound on the number of firings of rule r is
m
Ir + ( f j × I j )
j=1
Example 3 illustrates condition 1 of this algorithm. Example 11 illustrates condition 2 of this algorithm.
Example 11. A rule satisfying condition 2 of algorithm 2.
(p a
(c1 ^a1 1 ^a2 <y>)
(c2 ^a1 <x> ^a2 <y>)
-->
(modify 2 ^a2 <x>))
Suppose variables <x> and <y> have x and y items. The second condition element, (c2 ^a1 <x> ^a2 <y>), is the matched condition element. The enabling rules of this condition element can terminate in f1, f2, . . . , fm firings, respectively. We have up to Ia instantiations of rule a in the initial WM. Since the action does not affect the WMEs that satisfy the first condition element, (c1 ^a1 1 ^a2 <y>), there would be at most y instantiations when this rule is triggered by one of the enabling rules. The upper bound on the number of firings of rule a is
n
Ia + ( f j × y)
j=1
Problems Algorithm 2 is based on the ER graph. However, in the ER graph, we use the symbolic matching method to detect the enabling relations. Since the contents and interrelationship of WMEs cannot be determined statically, it is likely to cause a pessimistic prediction, as in example 12.
Example 12. A rule with pessimistic estimation.
(p a
(class_a ^a1 7 ^a2 <x>) (class_b ^b1 <x> ^b2 6)
-->
(make class_b ^b1 5 ^b2 4)) (p b
(class_a ^a1 { <x> <> <y> } ^a2 <y>) -(class_a ^a1 <y> ^a2 <x>)
(class_b ^b1 <x> ^b2 <y>) (class_b ^b1 <y> ^b2 <x>)
-->
(modify 3 ^b2 <x>))
392 TIMING ANALYSIS OF PREDICATE-LOGIC RULE-BASED SYSTEMS
First, the enabling conditions of rule b are quite restricted. They actually imply tight relationships among the WMEs of class a and class b. The probability of firing this rule is relatively low compared to other rules. However, we still need to say that rule a potentially enables rule b since rule a creates a WME (class b ^b1 5 ^b2 4), which can individually match the third and fourth condition elements of rule b.
Second, it is unlikely that the WME modified by rule a can match the second condition element of rule b, (class b ^b1 <x> ^b2 6), because of the constant restriction on attribute ^b2. However, since variable <x> in rule a is not semantically bounded, the enabling relation still weakly holds.
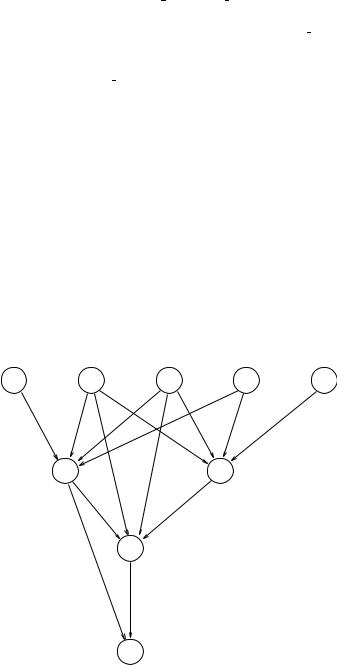
In addition, algorithm 2 does not take the control strategies (LEX or MEA) into consideration. These control strategies require the time tag of each WME in the WM to determine the priorities of each instantiation in the conflict set. The time tags of WMEs are hard to predict before run-time. Without knowing the time tag of the WMEs, it is difficult to predict the interference among instantiations. Thus we must assume no interference among instantiations to make a conservative estimation. If the domain is too large, our estimation becomes pessimistic. Figure 11.3 illustrates the situation. For example, rule c can be triggered by rules e, f , g, and h. It is rare or even impossible that instantiations of these four rules triggering rule c co-exist in the conflict set because firing one of these rules may prevent other rules from firing. For example, firing instantiations of rule e may remove the instantiations of rule f . Since we cannot predict the interference relation among rules e, f , g, and h, we must assume all instantiations of these four rules can be executed. The same condition applies to rules a, b, and d. As we can see, rule b inherits the firing bounds of rules
e |
f |
g |
h |
i |
c |
d |
b
a
Figure 11.3 Enabling relation with pessimistic estimation.
