
- •CONTENTS
- •PREFACE
- •LIST OF FIGURES
- •INTRODUCTION
- •1.1 WHAT IS TIME?
- •1.2 SIMULATION
- •1.3 TESTING
- •1.4 VERIFICATION
- •1.6 USEFUL RESOURCES
- •2.1 SYMBOLIC LOGIC
- •2.1.1 Propositional Logic
- •2.1.2 Predicate Logic
- •2.2 AUTOMATA AND LANGUAGES
- •2.2.1 Languages and Their Representations
- •2.2.2 Finite Automata
- •2.3 HISTORICAL PERSPECTIVE AND RELATED WORK
- •2.4 SUMMARY
- •EXERCISES
- •3.1 DETERMINING COMPUTATION TIME
- •3.2 UNIPROCESSOR SCHEDULING
- •3.2.1 Scheduling Preemptable and Independent Tasks
- •3.2.2 Scheduling Nonpreemptable Tasks
- •3.2.3 Nonpreemptable Tasks with Precedence Constraints
- •3.2.5 Periodic Tasks with Critical Sections: Kernelized Monitor Model
- •3.3 MULTIPROCESSOR SCHEDULING
- •3.3.1 Schedule Representations
- •3.3.3 Scheduling Periodic Tasks
- •3.4 AVAILABLE SCHEDULING TOOLS
- •3.4.2 PerfoRMAx
- •3.4.3 TimeWiz
- •3.6 HISTORICAL PERSPECTIVE AND RELATED WORK
- •3.7 SUMMARY
- •EXERCISES
- •4.1 SYSTEM SPECIFICATION
- •4.2.1 Analysis Complexity
- •4.3 EXTENSIONS TO CTL
- •4.4 APPLICATIONS
- •4.4.1 Analysis Example
- •4.5 COMPLETE CTL MODEL CHECKER IN C
- •4.6 SYMBOLIC MODEL CHECKING
- •4.6.1 Binary Decision Diagrams
- •4.6.2 Symbolic Model Checker
- •4.7.1 Minimum and Maximum Delays
- •4.7.2 Minimum and Maximum Number of Condition Occurrences
- •4.8 AVAILABLE TOOLS
- •4.9 HISTORICAL PERSPECTIVE AND RELATED WORK
- •4.10 SUMMARY
- •EXERCISES
- •VISUAL FORMALISM, STATECHARTS, AND STATEMATE
- •5.1 STATECHARTS
- •5.1.1 Basic Statecharts Features
- •5.1.2 Semantics
- •5.4 STATEMATE
- •5.4.1 Forms Language
- •5.4.2 Information Retrieval and Documentation
- •5.4.3 Code Executions and Analysis
- •5.5 AVAILABLE TOOLS
- •5.6 HISTORICAL PERSPECTIVE AND RELATED WORK
- •5.7 SUMMARY
- •EXERCISES
- •6.1 SPECIFICATION AND SAFETY ASSERTIONS
- •6.4 RESTRICTED RTL FORMULAS
- •6.4.1 Graph Construction
- •6.5 CHECKING FOR UNSATISFIABILITY
- •6.6 EFFICIENT UNSATISFIABILITY CHECK
- •6.6.1 Analysis Complexity and Optimization
- •6.7.2 Timing Properties
- •6.7.3 Timing and Safety Analysis Using RTL
- •6.7.5 RTL Representation Converted to Presburger Arithmetic
- •6.7.6 Constraint Graph Analysis
- •6.8 MODECHART SPECIFICATION LANGUAGE
- •6.8.1 Modes
- •6.8.2 Transitions
- •6.9.1 System Computations
- •6.9.2 Computation Graph
- •6.9.3 Timing Properties
- •6.9.4 Minimum and Maximum Distance Between Endpoints
- •6.9.5 Exclusion and Inclusion of Endpoint and Interval
- •6.10 AVAILABLE TOOLS
- •6.11 HISTORICAL PERSPECTIVE AND RELATED WORK
- •6.12 SUMMARY
- •EXERCISES
- •7.1.1 Timed Executions
- •7.1.2 Timed Traces
- •7.1.3 Composition of Timed Automata
- •7.1.4 MMT Automata
- •7.1.6 Proving Time Bounds with Simulations
- •7.2.1 Untimed Traces
- •7.2.2 Timed Traces
- •7.3.1 Clock Regions
- •7.3.2 Region Automaton
- •7.4 AVAILABLE TOOLS
- •7.5 HISTORICAL PERSPECTIVE AND RELATED WORK
- •7.6 SUMMARY
- •EXERCISES
- •TIMED PETRI NETS
- •8.1 UNTIMED PETRI NETS
- •8.2 PETRI NETS WITH TIME EXTENSIONS
- •8.2.1 Timed Petri Nets
- •8.2.2 Time Petri Nets
- •8.3 TIME ER NETS
- •8.3.1 Strong and Weak Time Models
- •8.5.1 Determining Fireability of Transitions from Classes
- •8.5.2 Deriving Reachable Classes
- •8.6 MILANO GROUP’S APPROACH TO HLTPN ANALYSIS
- •8.6.1 Facilitating Analysis with TRIO
- •8.7 PRACTICALITY: AVAILABLE TOOLS
- •8.8 HISTORICAL PERSPECTIVE AND RELATED WORK
- •8.9 SUMMARY
- •EXERCISES
- •PROCESS ALGEBRA
- •9.1 UNTIMED PROCESS ALGEBRAS
- •9.2 MILNER’S CALCULUS OF COMMUNICATING SYSTEMS
- •9.2.1 Direct Equivalence of Behavior Programs
- •9.2.2 Congruence of Behavior Programs
- •9.2.3 Equivalence Relations: Bisimulation
- •9.3 TIMED PROCESS ALGEBRAS
- •9.4 ALGEBRA OF COMMUNICATING SHARED RESOURCES
- •9.4.1 Syntax of ACSR
- •9.4.2 Semantics of ACSR: Operational Rules
- •9.4.3 Example Airport Radar System
- •9.5 ANALYSIS AND VERIFICATION
- •9.5.1 Analysis Example
- •9.5.2 Using VERSA
- •9.5.3 Practicality
- •9.6 RELATIONSHIPS TO OTHER APPROACHES
- •9.7 AVAILABLE TOOLS
- •9.8 HISTORICAL PERSPECTIVE AND RELATED WORK
- •9.9 SUMMARY
- •EXERCISES
- •10.3.1 The Declaration Section
- •10.3.2 The CONST Declaration
- •10.3.3 The VAR Declaration
- •10.3.4 The INPUTVAR Declaration
- •10.3.5 The Initialization Section INIT and INPUT
- •10.3.6 The RULES Section
- •10.3.7 The Output Section
- •10.5.1 Analysis Example
- •10.6 THE ANALYSIS PROBLEM
- •10.6.1 Finite Domains
- •10.6.2 Special Form: Compatible Assignment to Constants,
- •10.6.3 The General Analysis Strategy
- •10.8 THE SYNTHESIS PROBLEM
- •10.8.1 Time Complexity of Scheduling Equational
- •10.8.2 The Method of Lagrange Multipliers for Solving the
- •10.9 SPECIFYING TERMINATION CONDITIONS IN ESTELLA
- •10.9.1 Overview of the Analysis Methodology
- •10.9.2 Facility for Specifying Behavioral Constraint Assertions
- •10.10 TWO INDUSTRIAL EXAMPLES
- •10.10.2 Specifying Assertions for Analyzing the FCE Expert System
- •Meta Rules of the Fuel Cell Expert System
- •10.11.1 General Analysis Algorithm
- •10.11.2 Selecting Independent Rule Sets
- •10.11.3 Checking Compatibility Conditions
- •10.12 QUANTITATIVE TIMING ANALYSIS ALGORITHMS
- •10.12.1 Overview
- •10.12.2 The Equational Logic Language
- •10.12.3 Mutual Exclusiveness and Compatibility
- •10.12.5 Program Execution and Response Time
- •10.12.8 Special Form A and Algorithm A
- •10.12.9 Special Form A
- •10.12.10 Special Form D and Algorithm D
- •10.12.11 The General Analysis Algorithm
- •10.12.12 Proofs
- •10.13 HISTORICAL PERSPECTIVE AND RELATED WORK
- •10.14 SUMMARY
- •EXERCISES
- •11.1 THE OPS5 LANGUAGE
- •11.1.1 Overview
- •11.1.2 The Rete Network
- •11.2.1 Static Analysis of Control Paths in OPS5
- •11.2.2 Termination Analysis
- •11.2.3 Timing Analysis
- •11.2.4 Static Analysis
- •11.2.5 WM Generation
- •11.2.6 Implementation and Experiment
- •11.3.1 Introduction
- •11.3.3 Response Time of OPS5 Systems
- •11.3.4 List of Symbols
- •11.3.5 Experimental Results
- •11.3.6 Removing Cycles with the Help of the Programmer
- •11.4 HISTORICAL PERSPECTIVE AND RELATED WORK
- •11.5 SUMMARY
- •EXERCISES
- •12.1 INTRODUCTION
- •12.2 BACKGROUND
- •12.3 BASIC DEFINITIONS
- •12.3.1 EQL Program
- •12.3.4 Derivation of Fixed Points
- •12.4 OPTIMIZATION ALGORITHM
- •12.5 EXPERIMENTAL EVALUATION
- •12.6 COMMENTS ON OPTIMIZATION METHODS
- •12.6.1 Qualitative Comparison of Optimization Methods
- •12.7 HISTORICAL PERSPECTIVE AND RELATED WORK
- •12.8 SUMMARY
- •EXERCISES
- •BIBLIOGRAPHY
- •INDEX

CHAPTER 8
TIMED PETRI NETS
Petri nets were developed as an operational formalism for specifying untimed concurrent systems. They can show concurrent activities by depicting control and data flows in different parts of the modeled system. As an operational formalism, a Petri net gives a dynamic representation of the state of a system through the use of moving tokens. The original, classical, untimed Petri nets have been used successfully to model a variety of industrial systems. More recently, time extensions of Petri nets have been developed to model and analyze time-dependent or real-time systems. The fact that Petri nets can show the different active components of the modeled system at different stages of execution or at different instants of time makes this formalism especially attractive for modeling embedded systems that interact with the external environment.
8.1 UNTIMED PETRI NETS
A Petri net, or place-transition net, consists of four basic components: places, transitions, directed arcs, and tokens. A place is a state the specified system (or part of it) may be in. The arcs connect transitions to places and places to transitions. If an arc goes from a place to a transition, the place is an input for that transition and the arc is an input arc to that transition. If an arc goes from a transition to a place, the place is an output for that transition and the arc is an output arc from that transition. More than one arc may exist from a place to a transition, indicating the input place’s multiplicity. A place may be empty, or may contain one or more tokens. The state of a Petri net is defined by the number of tokens in each place, known as the marking and represented by a marking vector M. M[i] is the number of tokens in place i.
212
UNTIMED PETRI NETS |
213 |
Graphically, circles denote places, bars represent transitions, arrows denote arcs, and heavy dots represent tokens.
As an operational formalism, a Petri net shows a particular state of the system and evolves to the next state according to the following rules. Given a marking, a transition is enabled if the number of tokens in each of its input places is at least the number of arcs, ni , from the place to the transition. We select ni tokens as enabling tokens.
An enabled transition may fire by removing all enabling tokens from its input places and by putting in each of its output places one token for each arc from the transition to that place. If the number of input arcs and output arcs differs, the tokens will not be conserved. If two or more transitions are enabled, any transition may fire. The choice of the next-firing transition is nondeterministic. Each firing of a transition changes the marking and thus produces a new system state. Note that an enabled transition may fire, but is not forced (required) to fire.
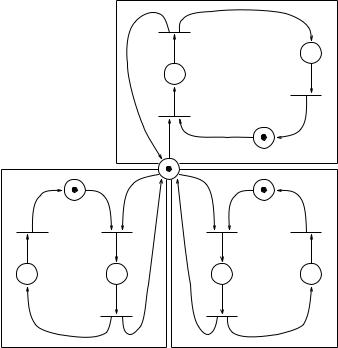
Example. Three-process mutual exclusion problem: Figure 8.1 shows the Petri net of the solution to a three-process mutual exclusion problem. There are 10 places in this net, three for each of the three tasks, and one “shared” among the three tasks.
T3
tn3
|
|
|
|
Pn3 |
|
|
|
Pcs3 |
|
|
|
|
|
|
|
tr3 |
|
|
|
tcs3 |
|
Pr3 |
|
|
|
|
|
|
|
|
|
Pmutex |
|
|
|
T1 |
Pr1 |
|
|
Pr2 |
T2 |
tr1 |
tcs1 |
|
tcs2 tr2 |
|
|
Pn1 |
Pcs1 |
|
Pcs2 |
Pn2 |
|
|
|
|
|
|
|
|
tn1 |
|
tn2 |
|
|
Figure 8.1 Petri net of a three-process mutual exclusion algorithm.
214 TIMED PETRI NETS
A dot in place Pni means that task Ti is in the non-critical region. A dot in place Pri means that task Ti is in the requesting (trying) region. A dot in place Pcsi means that task Ti is in the critical section. There are nine transitions in this net, three for each of the three tasks. The figure illustrates the state of the Petri net in which all three tasks are requesting to enter the critical section. This is indicated by dots in Pr1, Pr2, and Pr 3.
There are three enabled transitions in this net, tcs1, tcs2, and tcs3, since the input places of each transition contain tokens. The dot in place Pmutex indicates that one token (privilege) is available to grant to one task to enter and execute the critical section. The task to obtain this privilege is selected nondeterministically. Suppose task T1 is selected, then the transition tcs1 fires by removing the tokens from both of its input places and then putting a token in its output place Pcs1, indicating that task T1 is executing the critical section. Note that transitions tcs2 and tcs3 are now disabled since the token in Pmutex has been removed by the firing of tcs1.
After task T1 finishes executing its critical section, it goes back to its non-critical region. This is modeled by firing transition tn1, which removes the token in input place Pcs1, and then putting a token in its output place Pn1 and a token in its output place Pmutex. Now either T2 and T3 may be selected to enter the critical section since transitions tcs2 and tcs3 become enabled.
Given an initial state, the reachability set of a Petri net is the set of all states reachable from the initial state by a sequence of transition firings. To construct the reachability graph corresponding to a reachability set, we can represent each state by a node and add a directed edge from state s1 to state s2 if firing a transition enabled in state s1 leads the net to state s2.
8.2 PETRI NETS WITH TIME EXTENSIONS
Classical Petri nets cannot express the passage of time, such as durations and timeouts. The tokens are also anonymous and thus cannot model named items. They also lack hierarchical decomposition or abstraction mechanisms to properly model large systems. To model realistic real-time systems, several extended versions of Petri nets have been proposed to deal with timing constraints. There are basically two approaches: one associates the notions of time to transitions and the other associates time values to places.
[Ramchandani, 1974] associated a finite firing time to each transition in a classical Petri net to yield timed Petri nets (TdPNs). More precisely, the firing of a transition now takes time and a transition must fire as soon as it is enabled. TdPNs have been used mainly for performance evaluation. Shortly thereafter, [Merlin and Farber, 1976] developed a more general class of nets called time Petri nets (TPNs). These are Petri nets with labels: two values of time expressed as real numbers, x and y, are associated with each transition where x < y. x is the delay after which and y is the deadline by which to fire the enabled transition. A TPN can model a TdPn but not vice versa.
PETRI NETS WITH TIME EXTENSIONS |
215 |
8.2.1 Timed Petri Nets
A TdPN is formally defined as a tuple (P, T, F, V, M0, D) where
P is a finite set of places;
T is a finite, ordered set of transitions t1, . . . , tm ;
B is the backward incidence function B : T × P → N , where N is tghe set of nonnegative integers;
V : F → (P, T, F) is the arc multiplicity;
D : T → N assigns to every transition tI a nonnegative real number N indicating the duration of the firing of tI ; and
M0 is the initial marking.
A TdPN follows the following earliest firing schedule transition rule: An enabled transition at a time k must fire at this time if there is no conflict. Transitions with no firing durations (D(t) = 0) fire first. When a transition starts firing at time t it removes the corresponding number of tokens from its input places at time t and adds the corresponding number of tokens to its output places at time k + D(t). At any time, a maximal set of concurrently enabled transitions (maximal step) is fired.
8.2.2 Time Petri Nets
A TPN is formally defined as a tuple (P, T, B, F, M0, S) where
P is a finite set of places;
T is a finite, ordered set of transitions t1, t2, . . . , tm ;
B is the backward incidence function B : T × P → N , where N is the set of nonnegative integers;
F is the forward incidence function F : T × P → N ; M0 is the initial marking function M0 : P → N ;
S is the static interval mapping
S : T → Q × (Q ∞), where Q is the set of positive rational numbers.
[Merlin and Farber, 1976] specifies timing constraints on a transition ti using constrained static rational values as follows.
Static Firing Interval: Suppose αi S and βi S are rational numbers, then
S(ti ) = (αi S , βi S ),
where 0 ≤ αS < ∞, 0 ≤ βS ≤ ∞, and αS ≤ βS if βS = ∞ or αS < βS if βS = ∞.
The interval (αi S , βi S ) is the static firing interval for transition ti , indicated by the superscript S, where αi S is the static earliest firing time (EFT) and βS is the static
216 TIMED PETRI NETS
latest firing time (LFT). In general, for states other than the initial state, the firing intervals in the firing domain will be different from the static intervals. These dynamic lower and upper bounds are denoted αi and βi , respectively, and are called simply EFT and LFT, respectively.
Both the static and dynamic lower and upper bounds are relative to the instant at which ti is enabled. If ti is enabled at time θ, then while ti is continuously enabled, it must fire only in the time interval between θ + αi S (or θ + αi ) and θ + βi S (or
θ + βi ).
For modeling real-time systems, EFT corresponds to the delay before a transition can be fired, and LFT is the deadline by which a transition must fire. In Merlin’s model, time can be either discrete or dense. Also, the firing of a transition happens instantaneously; that is, firing a transition takes no time.
If there is no time interval associated with a transition, this transition is a classical Petri net transition and the time interval can be defined as αi S = 0, βi S = ∞. This indicates that an enabled transition may fire, but is not forced (required) to fire. Therefore, TPNs are timed restrictions of Petri nets.
TPN States: A state S of a TPN is a pair (M, I ) where M is a marking, and I is a firing interval set which is a vector of possible firing times.
For each transition enabled by marking M, a corresponding entry exists of the form (EFT,LFT) in I . Since the number of transitions enabled by a marking varies, the number of entries in I also varies as the Petri net runs. If the enabled transitions are ordered (numbered) in I , then entry i in I is the ith transition in the set of transitions enabled by M.
Example. For the example Petri net in Figure 8.1, M = Pr 1(1), Pr 2(1), Pr 3(1), Pmutex(1). Four places are marked, each containing one token. There are three enabled transitions: tcs1, tcs2, and tcs3. Suppose I has the following three time interval entries: (1, 6) (2, 7) (3, 8). Transition tcs1 may fire at any time between 1 and 6. Transition tcs2 may fire at any time between 2 and 7. Transition tcs3 may fire at any time between 3 and 8. Note that as soon as one transition fires, the other two become disabled.
Conditions for Firing Enabled Transitions Again, assuming the current TPN state S = (M, I ), a subset of the set of all enabled transitions may fire owing to the EFT and LFT timing restrictions on these transitions. Formally, a transition ti is firable from state S at time θ + δ iff both of the following conditions hold:
1.ti is enabled by marking M at time θ under the usual enabling condition of classical Petri nets; that is, p(M( p) ≥ B(ti , p)); and
2.δ is at least EFT of ti and at most the minimum of the LFTs of all transitions enabled by M; that is, EFT of ti ≤ δ ≤ min(LFTs of tk enabled by M).
PETRI NETS WITH TIME EXTENSIONS |
217 |
The reason for condition (2) is as follows. Suppose t j is the transition with the smallest LFT among all enabled transitions. Then t j must fire at time δ = LFT j if no other enabled transition has fired, modifying the marking and thus the state of the TPN.
The firing of a transition ti at relative time δ leads the TPN to a new state S = (M , I ), which can be derived as follows:
1. The new marking M is derived with the usual Petri nets rule: pM ( p) =
M ( p) − B(ti , p) + F(ti , p).
2.To derive the new set of time intervals I , we first remove from I the intervals associated with the transitions that are disabled after firing ti . Note that ti is also diabled after its firing. Then we shift the remaining time intervals by δ towards the origin of times, truncating them if necessary to obtain nonnegative
values. This corresponds to incrementing time by δ. Finally, we add to I the static intervals of the newly enabled transitions, yielding I . Thus the domain of the new state is the product of the time intervals of the remaining enabled transitions and those of the newly enabled transitions.
We use the following notation to denote that transition ti |
is firable from state S at |
||
time δ and its firing leads to state S : |
|
|
|
|
S −(ti→,δ) S . |
|
|
Firing Schedule: A firing |
schedule |
is a sequence of |
pairs (ti , δ1)(t2, δ2) · · · |
(tn , δn ). This schedule is feasible from state S iff states exist such that |
|||
(t1,δ1) |
(t2,δ2) |
(tn ,δn ) |
|
S −→ |
S1 −→ S2 |
· · · −→ Sn−1 −→ |
Sn . |
With this definition, we can construct the reachability graph to characterize the behavior of a TPN. However, as in other state space graphs, this reachability graph may have an infinite number of states and hence cannot be constructed in practice. Some simulation techniques that do not require the construction of the entire reachability graph have been proposed but are not appropriate for the analysis of safety-critical real-time systems. Later in this chapter we describe an efficient exhaustive analysis technique for a class of TPNs.
Example. For the example Petri net in Figure 8.1,
M0 = Pr1(1), Pr2(1), Pr 3(1), Pmutex(1).
I0 = (1, 8)(2, 7)(3, 6).
Therefore, any one of the three transitions tcs1, tcs2, tcs3 may fire according to the following timing restrictions. Transition tcs1 may fire in the period between relative time 1 (the EFT of (1,8)) and relative time 6 (the minimum of the LFTs (6,7,8) of the
218 TIMED PETRI NETS
intervals for the three enabled transitions). Similarly, transition tcs2 may fire in the period between relative time 2 (the EFT of (2, 7)) and relative time 6; and transition tcs3 may fire in the period between relative time 3 (the EFT of (3, 6)) and relative time 6. The choice of which transition to fire is nondeterministic.
Thus at any time δ1 within the infinite number of real values in interval (1, 6), firing tcs1 leads to state S1 = (M1, I1):
M1 = pcs1(1), pr 2(1), pr3(1) and
I1 = (1, 2).
Notice transitions tcs2 and tcs3 have been disabled by the firing of tcs1 and thus their associated time intervals are removed from I . Also, transition tcs1 is disabled after its own firing. Transition tn1 has enabled tcs1 and so the associated time interval (1, 2) is added to I .
Next, there is only one enabled transition to fire. Firing tn1 leads to state S2 =
(M2, I2):
M1 = pn1(1), pr 2(1), pr 3(1) and
I1 = (2, 4).
8.2.3 High-Level Timed Petri Nets
High-level timed Petri nets (HLTPNs), or time environment/relationship nets (TERNs) [Ghezzi et al., 1991], integrate functional and temporal descriptions in the same model. In particular, HLTPNs provide features that can precisely model the identities of a system’s components as well as their logical and timing properties and relationships. A HLTPN is a classical Petri net augmented with the following features.
For each place, a restriction exists on the type of tokens that can mark it; for example, each place has one or more types. If any type of token can mark a place, then this place has the same meaning as in a classical Petri net. Each token has a time-stamp indicating its creation time (or birth date) and a data structure for storing its associated data.
Each transition has a predicate that determines when and how the transition is enabled. This is similar to a transition in TPNs but is more elaborate. In HLTPNs, this predicate expresses constraints based on the values of the data structures and timestamps of the tokens in the input places. A transition also has an action that specifies the values of the data to be associated with the tokens produced by the transition firing. This action depends on the data and time-stamps of the tokens removed by the firing. Finally, a transition has a time function that specifies the minimum and maximum firing times. This function depends also on the data and time-stamps of the tokens removed by the firing. Graphically, a transition is represented by a box or rectangle.
PETRI NETS WITH TIME EXTENSIONS |
219 |
Environment/Relationship Nets We first more formally describe environment/relationship (ER) nets without timing extensions. Tokens in ER nets are environments, functions that associate values to variables. Each transition has an associated action that specifies the types of tokens for enabling the transitions and the types of tokens produced by the firing. More precisely, in an ER net:
1. Tokens are environments or possibly partial functions on I D and V : I D → V , where I is a set of identifiers and V is a set of values. ENV = V I D is the set of all environments.
2.Each transition t has an associated action, which is a relationship: α(t) ENVk(t) × ENVh(t), where k(t) and h(t) are the cardinalities of the preset and postset of transition t, respectively. The weight of each arc is 1. Also, h(t) > 0
for all t. The predicate of transition t, denoted π(t), is the projection of α(t) on ENVk(t).
3.A marking M is an assignment of multisets of environments to places.
4.In a marking M, a transition t is enabled iff for every input place pi of t, at least one token envi exists such that the enabling tuple env1, . . . , envk(t) π(t). More than one enabling tuple may exist for transition t, and a token may appear in more than one enabling tuple.
5.A firing is a triple x = enab, t, prod , where enab is the input tuple, prod is the output tuple, and enab, prod α(t).
6.In a marking M, the firing enab, t, prod occurs by removing the enabling
tuple enab from the input places of transition T and storing the tuple prod in the output places of transition T , thus producing a new marking, M .
7.A firing sequence starting from marking M0 is a finite sequence of firings,
enab1, t1, prod1 , · · · , enabn , tn , prodn ,
where t1 is enabled in M0 by enab1; each ti , i = 2, . . . , n, is enabled in Mi−1 by the firing enabi−1, ti−1, prodi−1 and its firing produces Mi .
Example. Figure 8.2 shows a sample ER net, which consists of three places and one transition with an action:
token1 = {x, −1 , y, 2}
token2 = {x, 2 , y, 2}
token3 = {x, 1 , y, 2}
act = {p1, p2 , p3|p1.x < p2.x p1.y = p2.y
p3.x = p1.x + p2.x p3.y = p1.y}
Only tokens token1 and token3 satisfy the predicate in the action act associated with the transition t since −1 < 1 and 2 = 2. Hence only these two tokens form an
