84 REAL-TIME SCHEDULING AND SCHEDULABILITY ANALYSIS
EXERCISES
1.Suppose a task consists of n subtasks Ji , each of which has computation time ci , i = 1, . . . , n. This task requests service at time k and has absolute deadline D. Give a formula to compute the latest deadline for completing each subtask such that the deadline of the entire task can be satisfied.
2.A scheduler is said to obey the stack discipline if whenever task A is preempted by task B, task A cannot resume execution before task B completes. A random scheduler is one that selects a task to execute every time unit by random choice. Does the random scheduler obey the stack discipline? Justify your answer clearly or give a counter-example.
3.The rate-monotonic scheduling algorithm is used to assign priority to the following task set. All tasks arrive at time 0.
task |
period |
computation time |
A |
30 |
1 |
B |
10 |
1 |
C |
6 |
1 |
D |
5 |
1 |
E |
2 |
1 |
(a)Show a schedule. What is the maximum response time for each task? Show all your calculations.
(b)If the periods of the tasks in a task set are all multiples of a base unit, say 4, is the static priority scheduler as good as the earliest deadline scheduler for this type of task set? Give a proof or show a counter-example.
4.Determine whether the following task set is RM-schedulable. If yes, show an RM schedule. All tasks arrive at time 0.
task |
period |
computation time |
A |
50 |
8 |
B |
20 |
3 |
C |
35 |
15 |
D |
10 |
2 |
5.Schedule the task set in exercise 3 using the FIFO (FCFS) scheduler. Is the schedule feasible?
6.Schedule the task set in exercise 3 using the EDF scheduler.
7.Schedule the task set in exercise 3 using the LL scheduler.
8.Show three periodic tasks that do not satisfy the simple schedulable utilization (Schedulability Test 2) but can still be RM-scheduled.
9.Construct a set of periodic tasks (showing start times, computation times, and periods) that can be scheduled by the EDF algorithm but not by the RM algorithm.
EXERCISES 85
10.Prove the optimality of the LL algorithm for a set of independent, preemptable tasks on a uniprocessor.
11.Under what condition(s) are the RM algorithm and the EDF algorithm equivalent?
12.There is an optimal priority-based scheduling algorithm for nonpreemptable tasks with arbitrary start times, computations times, and deadlines on a uniprocessor. Suppose the start times are 0 for all tasks in a task set. Is the EDF or LL algorithm optimal for this type of task set? Justify your answer.
13.Consider the following three periodic tasks:
T1: c1,1 = 1, c1,2 = 2, c1,3 = 3, d1 = p1 = 18.
T2: c2,1 = 1, c2,2 = 2, d2 = 5, p2 = 6.
T3: c3 = 1, d3 = p3 = 18.
T1 must rendezvous with T2 after the first, second, and third scheduling blocks.
T2 must rendezvous with T1 after the first scheduling block.
Construct a schedule for this task set.
14.Is it possible to find a set of n3 tasks which can be scheduled on a multiprocessor systems with n processors. Justify your answer.
15.Graphically show on a scheduling game board the three regions (R1(k), R2(k), R3(k)) of tasks defined in section 3.3.2. Describe the urgency of the tasks in each region.
16.The scheduling game board is a concise way of representing a scheduling problem at a particular instant of time. If tasks are not independent, that is, they have precedence constraints, then the existing game board representation and the execution rules as defined in the paper are not appropriate. Furthermore, the necessary and sufficient condition for scheduling tasks may no longer apply. Give an extension to the game board and the execution rules to handle precedence constraints, and suggest a technique and/or a new necessary and sufficient condition for scheduling.
17.Explain why there are “conflict sets” of tasks when we consider multiprocessor scheduling of independent tasks but there are no such conflict sets in uniprocessor scheduling.
18.Consider the sufficient condition for scheduling a set of periodic tasks: t must be integral. Is it still possible to schedule a set of periodic tasks if t is not integral but U (utilization) is less than n (number of processors). Justify your answer. If yes, show a task set and its schedule.
CHAPTER 4
MODEL CHECKING OF
FINITE-STATE SYSTEMS
One way to show that a program or system meets the designer’s specification is to manually construct a proof using axioms and inference rules in a deductive system such as temporal logic, a first-order logic capable of expressing relative ordering of events. This traditional, manual approach to concurrent program verification is tedious and error-prone even for small programs. For finite-state concurrent systems and systems that can be represented as such, we can use model checking instead of proof construction to check their correctness relative to their specifications.
In the model checking approach, we represent the concurrent system as a finitestate graph, which can be viewed as a finite Kripke structure. The specification or safety assertion is expressed in propositional temporal logic formulas. We can then check whether the system meets its specification using an algorithm called a model checker. In other words, the model checker determines whether the Kripke structure is a model of the formula(s). Several model checkers are available and they vary in code and run-time complexity. Here we describe one of the first model checkers, proposed by [Clarke, Emerson, and Sistla, 1986], and a more efficient symbolic model checker, developed later by [Burch et al., 1990a].
In Clarke, Emerson, and Sistla’s [1986] approach, the system to be checked is represented by a labeled finite-state graph and the specification is written in a propositional, branching-time temporal logic called computation tree logic (CTL). The use of linear-time temporal logic, which can express fairness properties, is ruled out since a model checker such as logic has high complexity. Instead, fairness requirements are moved into the semantics of CTL. In this chapter, we use the terms program and system interchangeably.
86
SYSTEM SPECIFICATION |
87 |
4.1 SYSTEM SPECIFICATION
To construct the finte-state graph corresponding to a given concurrent program, we have to thoroughly understand the program and determine the effect of each statement or action in the program. If a flow or control graph has been used in the design of the program, we can use it to determine the effect of each statement. One way to construct the finite-state graph is to begin with the initial state labeled with the initial values of all program variables or attributes, which are called labels here. Then for each possible next statement, we execute the statement and examine any change to one or more program variables. We construct a new state if it is different from any existing state. Note that sometimes we need to construct a new state even if its labels are the same as those in an existing state because the sequence of actions leading to the present state is different from that leading to the existing state. A directed edge is constructed from the state we are considering to the new state. We repeat this state and edge construction step for each new state until there are no states to consider. An example program and the corresponding finite-state graph in adjacency matrix form are shown in section 4.4.1.
For other systems that are not computer programs, we can perform a similar graph construction. First, we identify the state attributes that are relevant in the system to be specified in the CTL structure.
Example. In a railroad crossing scenario, the train has several possible positions: BEFORE-APPROACH means that the train has not been detected by the crossing sensor so it is far from the crossing, APPROACH means that the train has been detected by the crossing sensor and is approaching the crossing, BEFORE-CROSSING means that the train is near the crossing but is not on it yet, CROSSING means that the train is crossing and thus occupying the crossing intersection, and AFTERCROSSING means that the train has left the crossing. Therefore, the state attribute train-position has one of the above five values at a given time or state here. Next, we simulate or actually execute the possible actions in the system and observe the changes in the state attributes in a way similar to that of executing statements in a program and observing the changes in the program variables. We can then construct the finite-state graph as described above and shown in Figure 4.1.
Note that given a particular system to be specified, we can model it with the level of details required by our goal. In the railroad crossing example, each position of the train can be further divided into more precise numerical coordinates. This of course requires more states and transitions in the CTL structure, which in turn makes the analysis more complex.
The state-graph construction is very important since the correctness of the model checking depends on correctly capturing the concurrent program to be checked in the state graph. This construction is not discussed in [Clarke, Emerson, and Sistla, 1986] but an algorithm for it can be easily implemented [Cheng et al., 1993; Zupan and Cheng, 1994b] (see chapters 10 and 12). We first formally define the CTL structure.
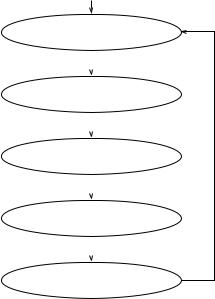
88 MODEL CHECKING OF FINITE-STATE SYSTEMS
S 0 |
(GATE_UP, BEFORE_APPROACH) |
|
S 1 |
|
|
|
|
|
(GATE_UP, APPROACH) |
||
S 2 |
|
|
|
|
|
(GATE_DOWN, NEAR_CROSSING) |
||
S 3 |
|
|
(GATE_DOWN, CROSSING) |
||
S 4 |
|
|
|
|
|
(GATE_DOWN, AFTER_CROSSING) |
||
Figure 4.1 CTL structure for the railroad crossing system.
CTL Structure: Formally, the CTL structure (state graph) is a triple, M =
(S, R, P), where
1.S is a finite set of states,
2.R is a binary relation on S which gives the possible transitions between states, and
3.P assigns to each state the set of atomic propositions true in that state.
The next step is to specify the specification or safety assertion in CTL.
CTL consists of a set AP of atomic propositions, which can be attributes such as C1 (process 1 in critical section), program variable value C = 1 (variable C has value 1), or BEFORE-CROSSING in the railroad crossing scenario. Every atomic proposition is a CTL formula. More complex CTL formulas can be constructed using the operators NOT, AND, AX, EX, AU, and EU. The operators NOT and AND have their usual meanings. To define the remaining operators, we need to define a path as an infinite, directed sequence of states (some of which may be the same) in the CTL structure.
The symbol X is the next-time operator. The formula AX f1 means that f1 holds in every immediate successor of the current program state. Alternatively, the formula EX f1 means that f1 holds in some immediate successor of the current program state. The symbol U is the until operator. The formula A[ f1 U f2] means that for every computation path there exists an initial prefix of the path such that f2 holds at the
CLARKE–EMERSON–SISTLA MODEL CHECKER |
89 |
last state of the prefix and f1 holds at all other states along the prefix. Alternatively, the formula E[ f1 U f2] means that for some computation path there exists an initial prefix of the path such that f2 holds at the last state of the prefix and f1 holds at all other states along the prefix.
To simplify the specification, we use the following abbreviations. AF( f ) means A[True U f ]: f holds in the future along every path from the initial state s0, so f is inevitable. EF( f ) means E[True U f ]: some path from the initial state s0 exists that leads to a state at which f holds, so f potentially holds. EG( f ) means NOT AF(NOT f ): some path from the initial state s0 exists on which f holds at every state. AG( f ) means NOT EF(NOT f ): f holds at every state on every path from the initial state s0, so f holds globally.
Figure 4.1 shows the finite-state graph of our simple railroad crossing system. Each state consists of two variables (gate-position, train-position). The initial state is s0.
4.2 CLARKE–EMERSON–SISTLA MODEL CHECKER
The Clarke–Emerson–Sistla (CES) model checker can determine whether a formula f0 written in CTL is true in a given CTL structure. It uses a compositional approach to analysis and hence operates in stages. The first stage checks all subformulas of length 1 in f0, that is, all atomic propositions. These atomic propositions hold in states having labels that are identical to these propositions. The second stage checks all subformulas of length 2 in f0 based on the results in stage 1, and labels each state with the subformulas that hold in that state, and so on. As a result, each state will be labeled with the set of subformulas of length less than or equal to i after the completion of the ith stage. At completion, the model checker will have checked the entire formula of length n.
The following data structures and functions [Clarke, Emerson, and Sistla, 1986] to access the labels associated with each state. The variables arg1 and arg2 refer to the first and second arguments of a binary temporal operator. The variable labeled[s][ f ] is true if state s is labeled with formula numbered f , false otherwise. The function addlabel(s, f, labeled) adds formula f to the current label of state s by modifying the array labeled.
To simplify the input of CTL formulas and internal processing, we use prefix notation to write the formulas. Now the length of a formula is equal to the total number of operands and operators in it. Suppose that formula f is assigned an integer i. If f is unary (e.g., f = NOT f1), then we assign the integers i +1 through i +length( f1) to the subformulas of f1. If f is binary (e.g., f = AU f1 f2), then we assign the integers i + 1 through i + length( f1) to the subformulas of f1 and i + length( f1) + 1 through i +length( f1) +length( f2) to the subformulas of f2. Using this assignment, in one pass through f , we can build two arrays, n f [length( f )] and s f [length( f )], where n f [i] is the ith subformula of f in the above numbering and s f [i] is the list of numbers assigned to the immediate subformulas of the ith formula. For example, if f = (AU (NOT CROSSING) GATE-DOWN), then n f and s f are
90 |
MODEL CHECKING OF FINITE-STATE SYSTEMS |
|
|
|
nf[1] (AU (NOT CROSSING) GATE-DOWN) |
sf[1] (2 4) |
|
|
nf[2] (NOT CROSSING) |
sf[2] (3) |
|
|
nf[3] |
CROSSING |
sf[3] nil |
|
nf[4] |
GATE-DOWN |
sf[4] nil. |
Therefore, we can determine in constant time the operator of a formula f and the numbers assigned to its arguments given f ’s number. This enables us to efficiently implement the function labelgraph. Instead of using the function labeled as in [Clarke, Emerson, and Sistla, 1986], we use the array labeled[][] and the initial array initlabeled[][], making the access and update faster. labeled[s][a] is true if state s is labeled with formula number a.
To handle an arbitrary formula f , we apply the labelgraph function to each subformula of f , starting with the highest numbered (simplest) formula and working backwards. Note that the indices in the following C code start from 0 instead of 1 since arrays in C are indexed from 0.
for (fi=flength; fi >= 1; fi--) labelgraph(fi,s,&correct);
The following C function labelgraph( f i, s, b) determines whether f i holds in state s. Note that it can handle seven cases: f i is atomic or has one of the following operators (NOT, AND, AX, EX, AU, or EU).
/*===========================================================================*/ /* function labelgraph */ /*===========================================================================*/
/* procedure labelgraph (fi,s,b) */ labelgraph (fi,s,b)
short fi, s; Boolean *b;
{
short i; switch(nf[fi-1][0].opcode)
{
case atomic: atf(fi,s,b); break;
case nt: ntf(fi,s,b); break;
case ad: adf(fi,s,b); break;
case ax: axf(fi,s,b); break;
case ex: exf(fi,s,b); break;
CLARKE–EMERSON–SISTLA MODEL CHECKER |
91 |
case au:
for (i=0; i <= numstates; i++) marked[i] = false;
for (i=0; i <= numstates; i++) if (!marked[i])
auf(fi,s,b);
break; case eu:
euf(fi,s,b);
break;
}
}
/*labelgraph*/
The following recursive C function auf( f i, s, b) determines whether the formula f i with an AU operator holds in state s. The code for initialization and for processing formulas with the other six operators is listed in section 4.5.
/*=========================================================================*/
/* |
function auf |
*/ |
/* |
In : fi = input formula number |
*/ |
/* |
s = state of the transition graph at which f is to be proved */ |
|
/* |
Out : b = true if formula f is true at state s |
*/ |
/* |
Description: |
*/ |
/* |
Use DFS to determine whether (au arg1 arg2) is true in state s |
*/ |
/*=========================================================================*/
/* procedure auf (fi,s,b) */ auf (fi,s,b)
short fi, s; Boolean *b;
{
short a1, a2, s1; Boolean b1;
a1 = sf[fi-1].arg1;
a2 = sf[fi-1].arg2; *b = true;
/*
#----------------------------------------------------------------------
#If s is marked, check to see if s is labeled with fi; return true
#if it is, else false.
#----------------------------------------------------------------------
*/
if (marked[s])
{
if (labeled[s][fi-1]) *b = true;
else *b = false;
}
92 MODEL CHECKING OF FINITE-STATE SYSTEMS
else
/*
#---------------------------------------------------------------------
#If the state has not been visited (marked), mark it and check to see
#if it is labeled with the argument 2.
#---------------------------------------------------------------------
*/ {
marked[s] = true;
if (labeled[s][a2-1] || initlabeled(s,nf[a2-1]))
{
addlabel(s,fi,labeled); *b = true;
}
else if (!(labeled[s][a1-1] || initlabeled(s,nf[a1-1])))
{
*b = false;
}
else {
/*
#----------------------------------------------------------
# For all successor states of s, check to see if f is true.
#----------------------------------------------------------
*/
s1 = 0;
while (*b && (s1 <= numstates))
{
if ((s != s1) && (e[s][s1] == 1))
{
auf(fi,s1,&b1); if (!b1)
*b = false;
}
s1 = s1 + 1;
}
if (*b) addlabel(s,fi,labeled);
}
}
}
/*auf*/
The function auf basically performs a depth-first search of the CTL structure starting from state s. It checks whether each path from s has a prefix with states labeled with the first argument of AU and eventually leading to a state labeled with the second argument of AU. It does so by labeling state s and the successor states of s that satisfy the formula fi, and then calling the function itself recursively to perform the same check. As soon as a state that is not labeled with the first argument is reached prior to reaching a state labeled with the second argument, the function returns false.