70 REAL-TIME SCHEDULING AND SCHEDULABILITY ANALYSIS
and k time units into the future. Then a necessary condition for scheduling to meet the deadlines of a set of tasks whose start times are the same (at time i = 0) is that for all k > 0, F (k, 0) ≥ 0.
Schedulability Test 9: For a multiprocessor system, if a schedule exists that meets the deadlines of a set of single-instance tasks whose start times are the same, then the same set of tasks can be scheduled at run-time even if their start times are different and not known a priori. Knowledge of pre-assigned deadlines and computation times alone is enough to schedule using the least-laxity-first algorithm.
A proof for this schedulability test can be found in [Dertouzos and Mok, 1989].
3.3.3 Scheduling Periodic Tasks
The preceding section shows that the LL scheduler is optimal for a set of singleinstance tasks satisfying a sufficient condition. This makes it possible to schedule tasks without knowing their release times in advance. This LL scheduler is no longer optimal for periodic tasks. Next, we present a simple sufficient condition for scheduling periodic tasks.
Simple Condition for Scheduling Periodic Tasks A simple sufficient condition is given in [Dertouzos and Mok, 1989] for feasible scheduling of a set of independent, preemptable, and periodic tasks on a multiprocessor system.
Schedulability Test 10: Given a set of k independent, preemptable (at discrete time instants), and periodic tasks on a multiprocessor system with n processors with
|
k |
ci |
|
|
|
|
|
|
U = |
|
|
≤ n, |
|
|
|
|
|
i =1 |
pi |
|
|
|
|
|
||
let |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T = GC D( p1, . . . , pk ), |
, . . . , T |
pk . |
||||||
t = GC D |
T , T |
p1 |
||||||
|
|
|
|
|
c1 |
|
|
ck |
A sufficient condition for feasible scheduling of this task set is t is integral.
If a task set satisfies Schedulability Test 10, it can be scheduled as follows. For each interval of T time units beginning at time 0, we schedule each task Ji , starting with task J1, for T (ci / pi ) time units. Therefore, within one period of task Ji , this task executes
|
p |
|
c |
|
|
i |
T |
i |
= ci |
T |
pi |
MULTIPROCESSOR SCHEDULING |
71 |
time units, which is the computation time of Ji . The length of each of these time slices pi /T is an integer owing to the definition of T . We begin by assigning tasks to processor 1 and “fill it up” until we encounter a task that cannot be scheduled on this processor. Then we assign it to processor 2. If processor 1 still has available time, we check to see if we can assign the next task to it. We repeat this procedure for the remaining tasks and processors. We are ready to show an example.
Example. Consider the following set of periodic tasks (period = deadline):
Task J1: c1 |
= 32, |
p1 |
= 40, |
Task J2: c2 |
= 3, |
p2 |
= 10, |
Task J3: c3 |
= 4, |
p3 |
= 20, and |
Task J4: c4 |
= 7, |
p4 |
= 10. |
Suppose two processors are available for executing these tasks. Is it possible to schedule these four tasks without missing a deadline?
Since the utilization of this task set is
|
4 |
ci |
32 3 4 7 |
|
|||||||
U = |
|
|
= |
|
+ |
|
+ |
|
+ |
|
= 2 ≤ n = 2, |
i =1 |
pi |
40 |
10 |
20 |
10 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
the necessary condition for scheduling is satisfied. Then we use the sufficient condition in Schedulability Test 10 to check if the task set is schedulable.
T = GC D(40, 10, 20, 10) = 10,
so
t = GC D |
10, 10 |
|
40 |
|
, 10 |
|
10 |
|
, 10 |
|
20 |
|
, 10 |
|
10 |
|
|
|
|
32 |
|
|
|
3 |
|
|
|
4 |
|
|
|
7 |
|
= GC D(8, 3, 2, 7) = 1.
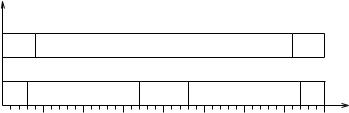
Therefore, since 1 is integral, a feasible schedule exists for this task set. One feasible schedule is shown in Figure 3.28.
Processor |
|
|
|
|
|
|
|
|
|
1 |
J3 |
|
|
J1 |
|
|
|
J3 |
|
2 |
J2 |
J4 |
|
J2 |
|
J4 |
|
J2 |
|
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
time |
|
Figure 3.28 Schedule for four periodic tasks on two processors.
72 REAL-TIME SCHEDULING AND SCHEDULABILITY ANALYSIS
In [Lee and Cheng, 1994], we consider the cost of task migration between processors and show that U ≤ n is both a necessary and sufficient condition for feasible scheduling for this type of task set.
3.4 AVAILABLE SCHEDULING TOOLS
A variety of tools are available for scheduling and schedulability analysis of real-time tasks. Here we review three such tools and report on our experience using them to schedule tasks in the NASA/International Space Station X-38 Crew Return Vehicle avionics [Rice and Cheng, 1999]. Although the X-38 task scheduling paradigm is not the dynamic scheduling example best supported by commercial scheduling tools, and no sporadic or asynchronous events seem to be present, the requirements for a tool to represent timing relationships of the system, deadlines, and the need for “what-if” analysis and workload adjustment nevertheless exist. Thus, the following tools are briefly and subjectively evaluated against supporting this particular project model:
1.PERTS (now renamed RAPID RMA),
2.PerfoRMAx, and
3.TimeWiz.
We outline the criteria and requirements for the scheduling tool evaluation and present a summary of each tool evaluation against the criteria:
1.ability to represent/model system,
2.ability to perform “what-if” schedulability analysis for changing workloads and to visualize deadlines,
3.ability to provide hardcopy reports of timelines representing system,
4.cost,
5.ease of use, and
6.maturity.
In addition to these evaluation criteria, we also provide information on the product, company, and platform for each scheduling tool.
3.4.1 PERTS/RAPID RMA
We examine a 30-day full-capability evaluation copy of PERTS (Prototyping Environment for Real-Time Systems), downloaded from the Tri-Pacific Software, Inc. web site
http://www.tripac.com
and installed on a SunOS 5.5.1 machine. PERTS is now renamed RAPID RMA, which provides Common Object Request Broker Architecture (CORBA) mapping
AVAILABLE SCHEDULING TOOLS |
73 |
capabilities, and interfaces to ObjecTime and Wind River’s WindView. PERTS provides a complete user documentation as well as a tutorial. The PERTS tool focuses on a task-resource model for the system, which is especially suited for the X-38 project, and provides a graphical means of depicting the system. The X-38’s 50-Hz critical task loop is modeled with the PERTS tool. The CPU resources, the Instrumentation Control Processor (ICP) and the Flight Critical Processor (FCP), are first modeled using the PERTS resource editor. We input information such as resource type, processing rate, and preemptability into the tool. Next, the 50-Hz flight critical tasks, the 50-Hz non-flight critical tasks, and a sample 10-Hz flight critical 10 Hertz task are defined in the PERTS task editor.
Attributes such as task name, ready time, deadline, period, workload, and resource(s) utilized are defined for each task. Dependencies between tasks, even on different CPU resources, such as what is required to ensure proper sequencing for X-38 tasks, are easily and graphically represented. A robust set of scheduling, sporadic server, and resource sharing policies are provided in the tool, though only a fixed-priority periodic user-defined scheduling policy across two nodes is required to model the X-38 task system. Because of the deterministic task execution times required in this system, the full power of the scheduling algorithms provided is not utilized. Rather, to ensure a set task execution order, user-specified priorities as well as a phase-offset start time for each task are manually assigned.
PERTS provides the capability for singleand multi-node schedulability analysis across multiple resources, which is precisely what is needed for the X-38 system. The ability to schedule between each of the two processors, the ICP and the FCP, in a Flight Critical Chassis (FCC) and represent dependencies between tasks running on these different resources is required and is provided by the PERTS tool. Singlenode analysis is performed running the task set as described above, and the tool graphically shows a 50% CPU utilization for the FCP, which is what is expected. After running a schedule, a display that combines all resources and tasks on a single timeline is produced.
Of all the tools evaluated, the task-resource model provided by this tool is especially useful for modeling the X-38 system. By increasing workloads or changing start times, it is verified that the PERTS tool meets the requirement for schedulability analysis. A task set that is not schedulable is clearly identified as such. The timeline display gives a clear block diagram but does not provide the timeline hardcopy/reporting capability necessary for team communication. Only a screen print is available for hardcopy output. In general, the tool is intuitive, is rich in analysis capability, and seems to have the greatest maturity of all tools evaluated, and taken as is, it best met our scheduler tool evaluation criteria listed above.
3.4.2 PerfoRMAx
We examine an evaluation copy of PerfoRMAx downloaded from the AONIX web site
http://www.aonix.com