
- •1.Основные задачи сопротивления материалов.
- •2.Допущения принятые в сопротивлении материалов.
- •3.Геометрическая схематизация элементов строительных конструкций.
- •4.Классификация сил, действующих на элемент конструкции.
- •5.Внутренние силы.
- •Простейшие случаи сопротивления
- •6.Деформация и перемещения.
- •7.Расчетная схема.
- •8.Продольная сила и её определение. Построение эпюры продольной силы.
- •9.Напряжения при растяжении-сжатии (нормально напряжение). Построение эпюры нормальных напряжений.
- •10.Закон Гука при растяжении-сжатии. Модуль упругости (модуль Юнга).
- •Определение абсолютной деформации участка бруса
- •11.Коэффициент поперечной деформации (коэффициент Пуассона
- •12.Определение перемещений при растяжении-сжатии. Закон Гука для участка бруса. Определение перемещений сечений бруса
- •13.Определение механических характеристик материалов. Испытание на растяжение. Испытание на сжатие.
- •14.Методы расчёта элементов конструкций на прочность и жесткость.
- •15.Статические неопределимые задачи при растяжении-сжатии и методы их решения.
- •16.Особенности стержневых статически неопределимых конструкций.
- •17.Сдвиг. Поперечная сила.
- •18.Напряжение при сдвиге (касательное напряжение). Закон парности касательных напряжений.
- •19.Закон Гука при сдвиге. Модуль упругости при сдвиге. Связь модуля при сдвиге с модулем при растяжении.
- •20.Практические расчёты на сдвиг. Расчет сварных соединений. Расчёт болтовых и заклёпочных соединений.
- •21.Геометрические характеристики плоских сечений. Общие сведения. Статический момент сечения. Определение центра тяжести сечения.
- •22.Моменты инерции площади сечения.
- •23.Зависимость между моментами инерции относительно параллельных осей. Вычисление моментов инерции сложных сечений.
- •24.Зависимость между моментами инерции при повороте осей. Главные оси и главные моменты инерции.
- •Главные оси инерции и главные моменты инерции
- •25.Вычисление главных центральных осевых моментов инерции простых сечений.
- •26.Вычисление главных центральных осевых моментов инерции сложных сечений.
- •28.Напряжения при кручении (вывод формулы).
- •29.Определение перемещений при кручении.
- •30.Практические расчёты на кручение.
- •31.Изгиб. Внутренние усилия при изгибе. Разновидности изгиба. Виды балок.
- •32.Определение внутренних усилий при изгибе. Дифференциальные зависимости при изгибе. Правила построения эпюр.
- •34.Касательные напряжения при изгибе (вывод формулы).
- •35.Расчёт на прочность при изгибе.
- •36.Расчёт балок на жёсткость. Методы определения перемещений при изгибе (перечислить методы).
- •37.Определение перемещений при помощи дифференциального уравнения изогнутой оси балки..
- •38.Определение перемещений при изгибе при помощи универсального уравнения изогнутой оси бруса (метода начальных параметров).
- •39.Определение перемещений при изгибе при помощи интеграла Мора. Правило Верещагина.
- •Потенциальная энергия системы с учетом силы ф
- •Площадь иногда приходится разбивать на более простые части, тогда вместо (20) получим
- •40.Напряжённое состояние в точке элемента конструкции. Виды напряжённого состояния.
- •41.Линейное напряжённое состояние. Плоское напряжённое состояние.
- •Внецентренное растяжение (сжатие) прямого бруса.
- •Ядро сечения
- •43Изгиб с кручением.
- •44.Изгиб, кручение и сжатие.
14.Методы расчёта элементов конструкций на прочность и жесткость.




15.Статические неопределимые задачи при растяжении-сжатии и методы их решения.
Статически неопределимыми называются брусья и системы, внутренние усилия или реакции опор в которых нельзя определить с помощью одних лишь уравнений равновесия. Поэтому при их расчете необходимо составлять дополнительные уравнения – уравнения совместности деформаций или перемещений сечений, учитывающих характер деформации системы (геометрическая сторона задачи). Число дополнительных уравнений, необходимых для расчета системы, характеризует степень ее статической неопределимости. Всегда можно составить столько дополнительных уравнений, сколько не хватает уравнений статики для решения задачи.
Усилия в элементах статически определимых систем возникают только от действия внешней нагрузки (включая собственный вес конструкций). В элементах статически неопределимых систем усилия могут возникать и при отсутствии внешней нагрузки – в результате, например, изменения температуры, смещения опорных связей, а также при монтаже из-за неточности изготовления отдельных элементов конструкции.
Составление дополнительных (к уравнениям равновесия) уравнений перемещений (геометрическая сторона задачи) рассмотрим на примере.
Стержень защемлен по концам и нагружен силой F, действующей вдоль оси стержня (рис. 3.9). Собственный вес стержня не учитываем.

Под действием силы F в этом случае в заделках могут возникать только показанные реакции VA и VB, которые требуется определить. Направления неизвестных опорных реакций выбираем произвольно.
Для данного случая (когда все силы действуют вдоль одной прямой) можно составить только одно уравнение равновесия:
![]()
![]()
Для определения двух неизвестных VA и VB необходимо составить дополнительно одно уравнение, т.е. рассматриваемая задача является статически неопределимой (степень статической неопределимости бруса равна единице).
Для
составления дополнительного уравнения
рассмотрим геометрическую
сторону задачи – составим условие
совместности деформаций отдельных
участков: общая длина бруса не может
изменяться, следовательно,
![]()
Удлинение
![]() можно выразить как сумму удлинений двух
участков:
можно выразить как сумму удлинений двух
участков:
![]() (3.18)
(3.18)
Рассмотрим
физическую
сторону задачи
и абсолютные удлинения участков
![]() и
и![]() ,
используя закон Гука по формуле (3.13),
выразим через продольные силы N1
и
N2:
,
используя закон Гука по формуле (3.13),
выразим через продольные силы N1
и
N2:
![]()
![]() (3.19)
(3.19)
В
этих формулах
![]() и
и![]() представляют собой выражения продольных
сил на участках 1 и 2, записываемые по
методу сечений:
представляют собой выражения продольных
сил на участках 1 и 2, записываемые по
методу сечений:
![]()
![]() (3.20)
(3.20)
Подставим выражения (3.19) с учетом (3.20) в формулу (3.18) и получим:
![]() (3.21)
(3.21)
Отсюда
найдем
![]() =
=![]()
При
условии
![]() получим:
получим:
![]() (3.22)
(3.22)
Если
![]() то
то![]() (3.23)
(3.23)
Если
![]() то
то![]()
![]() (3.24)
(3.24)
Реакцию
![]() найдем из уравнения статики:
найдем из уравнения статики:
![]() (3.25)
(3.25)
При равномерном изменении температуры окружающей среды вокруг бруса на t формулы (3.19) запишутся в виде:
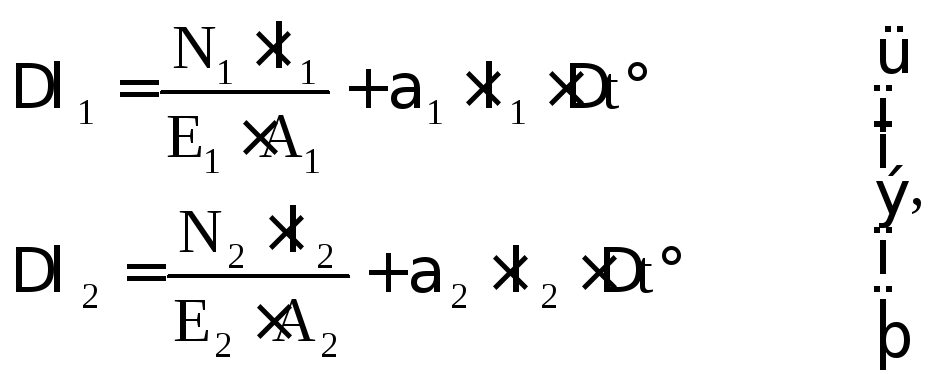 (3.26)
(3.26)
где 1 и 2 – коэффициенты линейного расширения материалов бруса.
Подставляя формулы (3.26) в формулу (3.18) и используя (3.20), найдем реакцию VB при совместном воздействии на брус силы F и изменением температуры окружающей среды на t градусов.
