
- •1.Основные задачи сопротивления материалов.
- •2.Допущения принятые в сопротивлении материалов.
- •3.Геометрическая схематизация элементов строительных конструкций.
- •4.Классификация сил, действующих на элемент конструкции.
- •5.Внутренние силы.
- •Простейшие случаи сопротивления
- •6.Деформация и перемещения.
- •7.Расчетная схема.
- •8.Продольная сила и её определение. Построение эпюры продольной силы.
- •9.Напряжения при растяжении-сжатии (нормально напряжение). Построение эпюры нормальных напряжений.
- •10.Закон Гука при растяжении-сжатии. Модуль упругости (модуль Юнга).
- •Определение абсолютной деформации участка бруса
- •11.Коэффициент поперечной деформации (коэффициент Пуассона
- •12.Определение перемещений при растяжении-сжатии. Закон Гука для участка бруса. Определение перемещений сечений бруса
- •13.Определение механических характеристик материалов. Испытание на растяжение. Испытание на сжатие.
- •14.Методы расчёта элементов конструкций на прочность и жесткость.
- •15.Статические неопределимые задачи при растяжении-сжатии и методы их решения.
- •16.Особенности стержневых статически неопределимых конструкций.
- •17.Сдвиг. Поперечная сила.
- •18.Напряжение при сдвиге (касательное напряжение). Закон парности касательных напряжений.
- •19.Закон Гука при сдвиге. Модуль упругости при сдвиге. Связь модуля при сдвиге с модулем при растяжении.
- •20.Практические расчёты на сдвиг. Расчет сварных соединений. Расчёт болтовых и заклёпочных соединений.
- •21.Геометрические характеристики плоских сечений. Общие сведения. Статический момент сечения. Определение центра тяжести сечения.
- •22.Моменты инерции площади сечения.
- •23.Зависимость между моментами инерции относительно параллельных осей. Вычисление моментов инерции сложных сечений.
- •24.Зависимость между моментами инерции при повороте осей. Главные оси и главные моменты инерции.
- •Главные оси инерции и главные моменты инерции
- •25.Вычисление главных центральных осевых моментов инерции простых сечений.
- •26.Вычисление главных центральных осевых моментов инерции сложных сечений.
- •28.Напряжения при кручении (вывод формулы).
- •29.Определение перемещений при кручении.
- •30.Практические расчёты на кручение.
- •31.Изгиб. Внутренние усилия при изгибе. Разновидности изгиба. Виды балок.
- •32.Определение внутренних усилий при изгибе. Дифференциальные зависимости при изгибе. Правила построения эпюр.
- •34.Касательные напряжения при изгибе (вывод формулы).
- •35.Расчёт на прочность при изгибе.
- •36.Расчёт балок на жёсткость. Методы определения перемещений при изгибе (перечислить методы).
- •37.Определение перемещений при помощи дифференциального уравнения изогнутой оси балки..
- •38.Определение перемещений при изгибе при помощи универсального уравнения изогнутой оси бруса (метода начальных параметров).
- •39.Определение перемещений при изгибе при помощи интеграла Мора. Правило Верещагина.
- •Потенциальная энергия системы с учетом силы ф
- •Площадь иногда приходится разбивать на более простые части, тогда вместо (20) получим
- •40.Напряжённое состояние в точке элемента конструкции. Виды напряжённого состояния.
- •41.Линейное напряжённое состояние. Плоское напряжённое состояние.
- •Внецентренное растяжение (сжатие) прямого бруса.
- •Ядро сечения
- •43Изгиб с кручением.
- •44.Изгиб, кручение и сжатие.
28.Напряжения при кручении (вывод формулы).
В поперечном сечении бруса возникают только касательные напряжения от крутящего момента, определяемые по формуле (6.1). Их направление в каждой точке перпендикулярно радиусу, соединяющему эту точку с центром сечения (рис. 6.1). В центре (при ρ = 0) касательные напряжения равны нулю; в точках же, расположенных в непосредственной близости от внешней поверхности бруса, они наибольшие.
![]() (6.1)
(6.1)
где
![]() – крутящий момент в рассматриваемом
сечении;
– крутящий момент в рассматриваемом
сечении;![]() – полярный момент инерции круглого
поперечного сечения;К
– расстояние от центра тяжести сечения
до рассматриваемой точки К (рис. 6.1).
– полярный момент инерции круглого
поперечного сечения;К
– расстояние от центра тяжести сечения
до рассматриваемой точки К (рис. 6.1).
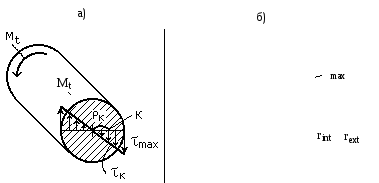
Рис. 6.1
Эпюры
![]() ,
построенные по формуле (6.1) для круглого
сплошного и кольцевого сечений,
представлены на рис. 6.1а, б.
,
построенные по формуле (6.1) для круглого
сплошного и кольцевого сечений,
представлены на рис. 6.1а, б.
Наибольшие касательные напряжения в поперечных сечениях определяются по формуле:
![]() (6.2)
(6.2)
Введем следующее обозначение:
![]() (6.3)
(6.3)
где
![]() –
называется полярным моментом сопротивления
поперечного сечения (см3,
м3);
–
называется полярным моментом сопротивления
поперечного сечения (см3,
м3);
![]() – расстояние от центра тяжести до
наиболее удаленной точки сечения, оно
равняется радиусу круга
– расстояние от центра тяжести до
наиболее удаленной точки сечения, оно
равняется радиусу круга![]()
Условие прочности при кручении запишется:
![]() (6.4)
(6.4)
где RS – расчетное сопротивление материала при сдвиге.
29.Определение перемещений при кручении.

30.Практические расчёты на кручение.
Условие прочности бруса при кручении заключается в том, что наибольшее касательное напряжение, возникающее в нем, не должно превышать предельно допустимое. При этом расчетная формула на прочность имеет вид:
τmax = Мкр / Wr ≤ [τкр],
где [τкр] - предельное допускаемое напряжение.
При практических расчетах, определяя предельные допускаемые напряжения для различных материалов, используют зависимость между напряжениями при растяжении и напряжениями при кручении, которая для стали и чугуна имеет вид:
для стали - [τкр] = 0,55....0,6 [σр]
для чугуна - [τкр] = 1,0....1,2 [σр])
(здесь [σр] - справочная или определяемая экспериментально величина, (предельное допустимое напряжение растяжения) характеризующая материал бруса (вала).
Кроме требования прочности к валам предъявляются требования жесткости, которое заключается в том, что угол закручивания участка вала длиной 1 м не должен превышать предельной величины, определяемой требованиями конструкции. Допускаемый угол закручивания 1 м длины вала задается в градусах и обозначается [φ0°].
Расчетная формула на жесткость при кручении имеет вид:
φ0°= 180 Мкр / (пGIr) ≤ [φ0°]
В реальных механизмах обычно допускаются углы закручивания валов в пределах [φ0°] = 0,25...1 градус/м.
31.Изгиб. Внутренние усилия при изгибе. Разновидности изгиба. Виды балок.
Под
изгибом понимается такой вид нагружения,
при котором в поперечных сечениях бруса
возникают изгибающие моменты Mx
или
My .
Если изгибающий момент в сечении является
единственным силовым фактором, то
изгиб называется чистым
(рис. 5.1, а).
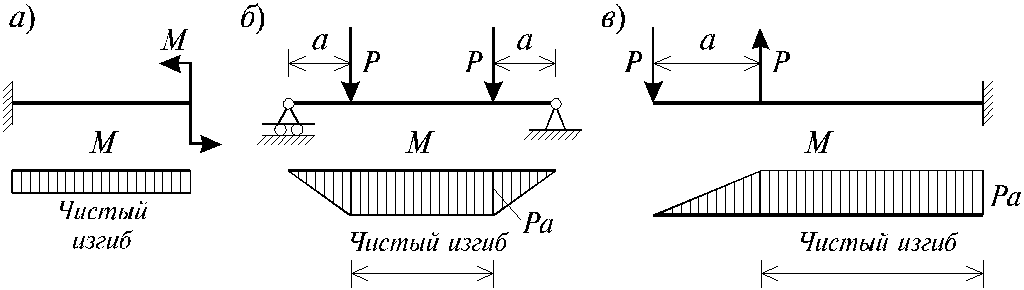
Рис. 5.1
В тех случаях, когда в поперечных сечениях бруса наряду с изгибающим моментом возникают и поперечные силы изгиб называется поперечным. Брус, работающий в основном на изгиб, часто называют балкой. В дальнейшем будем рассматривать такие случаи изгиба балки, при которых, вопервых, поперечное сечение балки имеет хотя бы одну ось симметрии, и, вовторых, вся нагрузка лежит в плоскости, совпадающей с осью симметрии балки. Таким образом, одна из главных осей инерции лежит в плоскости изгиба, а другая перпендикулярна ей.
Для того, чтобы правильно ориентироваться в вопросах, связанных с расчетом бруса на изгиб, необходимо прежде всего научиться определять законы изменения внутренних силовых факторов, т.е. научиться строить эпюры изгибающих моментов и поперечных сил.
Предварительно рассмотрим три основных типа опорных связей балки с основанием:
1. Шарнирноподвижная опора (рис. 5.1, б левая опора балки), ограничивающая лишь вертикальное перемещение опорного узла.
2. Шарнирнонеподвижная опора (рис. 5.1, б правая опора балки), ограничивающая вертикальное и горизонтальное перемещения опоры.
3. Жесткая заделка (рис. 5.1, а опора балки на левом краю), не допускающая поворота и перемещений по вертикали и горизонтали сечения балки, примыкающего к опоре.
По запрещенным направлениям во всех этих типах опор возникают соответствующие реакции.
Закрепленные опорами балки имеют следующие названия:
а) однопролетная или двухопорная (рис. 1.9);
б) консоль (рис.1.10);
в) консольная балка (рис. 1.11)
|
Рис. 1.9 |
Рис. 1.10 |
Рис.1.11 |



