4. Выявление влияния отдельных факторов на изучаемый.

Применение методов корреляционного анализа даёт возможность выражать связь между признаками аналитически и придавать количественное значение. К примеру, связь между признаками может быть выражена уравнением прямой: . В уравнении прямой х всегда известен, поэтому нужно найтии, представляющие собой среднее значение некоторых показателей, принимаемые в уравнении постоянными. Известно, что параметр а_о является отрезком ординаты при х=0, а а₁=tg угла наклона. Нахождение параметров производится по способу выравнивания наименьших квадратов. Линия связи должна обладать основными сво-вами ср.арифм: ∑d=0, ∑d²=min; если обозначить ординаты фактических точек поля корреляции через y_i, а ординаты теоретических линий - , то второе условие можно записать так:. Это условие и лежит в основе способа наименьших квадратов. Поскольку, то:. Вычислив первые производные поиот этой ф-ии и приравняв каждую из производных к 0, мы сможем определить те значенияипри которыхбудет минимальной. После преобразований получим систему из 2ух уравнений: 1),

2) . Для нахожденииинужно найти ∑х, ∑у, ∑х², ∑ху (данные берутся из представленной таблицы). Подставляя значения из предоставленной таблицы находим и, затем эти значения подставляем в ур-ие.

Параметры итакже можно определить по формулам:,.

Связь между признаками прямая, поэтому нужно разработать мероприятие по усилению влияния фактора. Может быть криволинейная зависимость между признаками: парабола, гипербола. Способ решения будет аналогичен. Кроме парной корреляции можно вычислить зависимость одно признака от нескольких, т.е. мы будем иметь уравнение множественной регрессии.

5. Множественная корреляция.

Методология решения задач множественной корреляции: установление наличия связи, установление тесноты связи, формы связи, влияние отдельных факторов на общий результат. Отличительные особенности этой методологии: иногда приходится укрупнять единицы наблюдения (брать не рабочих, а бригады; не строительные управления, а тресты); численность исследуемой совокупности должна превосходить число факторов в 6-7 раз; должен быть тщательный отбор факторов и их содержательный анализ д/выбора уравнения связи. Д/этого вычисляют х, σ, σ²_, v и коэфф-т тесноты связи. Существенным в составлении уравнения регрессии является выбор типа функции. Модель должна иметь математическое решение → её нужно выразить в форме одной из известных функций. Как и при парной корреляции, указание на функций можно получить из логического анализа предыдущего опыта, экспертных оценок, изучение исходных эмпирических данных. Чаще всего д/определения вида уравнения связи исп-ся способ перебора различных уравнений: большое число уравнений связи реализуется на ЭВМ с помощью специально разработанного алгоритма перебора с последующей проверкой, главным образом на основе критерия Стьюдента (очень трудоёмко).

Д/определения тесноты связи при множественной корреляции пользуются коэффициентом множественной корреляции предварительно вычислив парной корреляции. Если х зависит от у и z, то парные коэфф-ты вычисляют по формулам:,,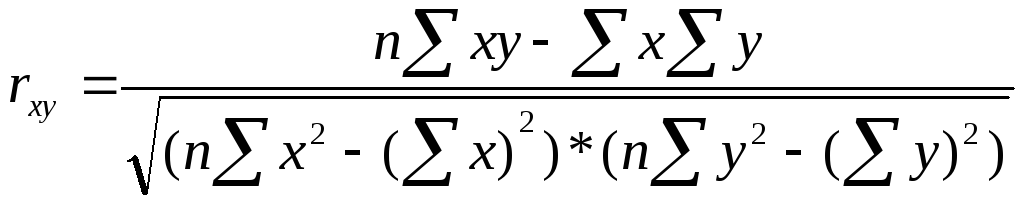

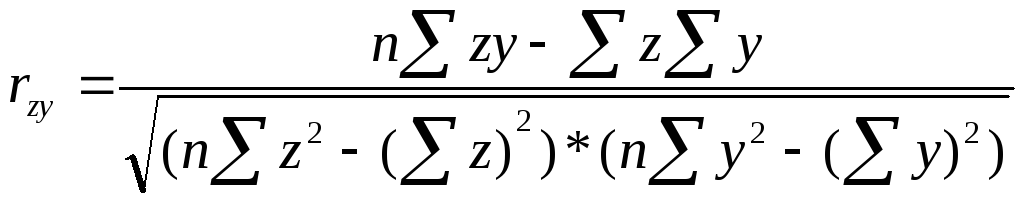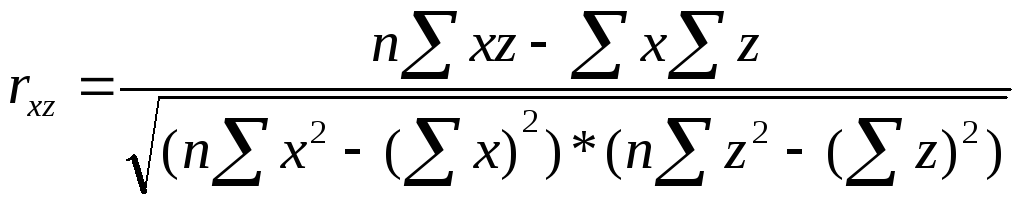
На их основе вычисляют коэфф-т множественной корреляции: