2. Различные виды приближений. Интерполяция и аппроксимация.

Аппроксимация заключается в том, что используя имеющуюся информацию по f(x) можно рассмотреть другую функцию ц(ч) близкую в некотором смысле к f(x), позволяющую выполнить над ней соответствующие операции и получить оценку погрешность такой замены. ц(х)- аппроксимирующая функция. Интерполяция (частный случай аппроксимации)

Интерполяция – один из способов аппроксимации данных. В простейшем (одномерном) случае задача интерполяции [1-3] состоит в следующем: заданы точки (x_i, y_i), и требуется найти функцию(x), которая проходит через эти точки (см. рис. 1),

т.е.

(x_i)= y_i , .                (1)

Точки (x_i, y_i) называют узлами интерполяции, а функцию (x) – интерполирующей функцией или интерполянтом. Вид функции (x) определяет способ интерполяции. На практике в качестве интерполирующей функции (x) часто используются алгебраические полиномы различного вида, так как полиномы легко вычислять, дифференцировать и интегрировать. При этом интерполяция носит название полиномиальной.

3. Методы конечных элементов, граничных элементов, их сравнительные преимущества и недостатки.

МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

Метод конечных элементов несколько подобен методу конечных разностей. Однако он имеет вариационные особенности в алгоритме и содержит несколько гибких особенностей. В методе конечных элементов, вместо частных дифференциальных уравнений с граничными условиями, соответствующие функционалы составляют систему вариационных выражений, относящихся к каждой из малых областей или объемов, подразделяющих область, представляющую интерес. Обычно, эти малые сегменты - многоугольники типа треугольников и прямоугольников для двух размерных задач и тетраэдных элементов для трехмерных задач. Из-за такой дискретизации, не всякие ограничения могут быть наложены на форму структуры.

Сущность этого метода иллюстрируется ниже для задачи уравнения Лапласа(1) в двумерной области на рис. 2. Решение (1), подчиненного граничному условию эквивалентно к минимизации функционала

(4)

Этот интеграл выполнен как сумма вкладов из всех малых многоугольных (треугольных в этом примере) областей. В каждом многоугольнике  может быть аппроксимирована полиномом по x и y:

Рис. 2. Типичное подразбиение поперечного сечения в двумерном анализе методом конечных элементов.

Коэффициенты имогут быть выражены в терминах значенийв каждой вершине треугольника:где нижний индексp = i, j, k идентифицирует три вершины. Поскольку только требуются для вычисления (4), оно переписывается как

                       

Значение I( ) для одного многоугольника

                (5)

 где индекс t указывает операцию транспонирования, а | S| - площадь многоугольника, равная

                   

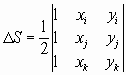
Для минимизации используется метод Релея-Ритца.

                (6)

Подстановка (5) в (6) приводит к результату

Когда этот процесс применяется ко всем многоугольникам в S, получаем

(7)

Так как некоторые из , расположенные на границе, известны, (7) может быть решено для потенциалов во всех внутренних точках. Алгоритмы для волновых уравнений для двух и трех координат были разработаны [8]. Одна из проблем методов конечных элементов - существование так называемых паразитных нулей. Такие нули соответствуют физически несуществующим структурам. Точная причина этого явления еще не ясна. Несколько способов имеется, чтобы уменьшить влияние или исключить эти нули. Обычно они основаны на вариационном выражении, которое содержит дополнительное ограничение

Некоторая предосторожность должна быть осуществлена, когда метод конечных элементов применяется к задаче с открытой областью типа диэлектрического волновода. Во многих случаях, область, к которой метод применяется, усекается в конечном объеме. В некоторых ситуациях, например, вблизи граничной частоты волновода, такое усечение не очевидно, потому что область разделяется очень медленно

В свое время был предложен метод граничных элементов [10,11]. Это - комбинация метода интегрального уравнения на границе, и техники дискретизации, подобной алгоритму конечных элементов, применяемому к границе. По существу, волновое уравнение для объема преобразовано к интегральному уравнению посредством тождества Грина. Поверхностные интегралы - дискретизированы на N сегментах, и их расчет в каждом сегменте выполняется после того, как величины поля аппроксимированы многочленами.

Одно из преимуществ этого метода состоит в уменьшении требуемой памяти и времени расчета, следующее из уменьшения размерности.