
- •Оглавление
- •Глава 5. Пространственная система сил..........................................27
- •Глава 6. Кинематика точки........................................................................31
- •Глава 7. Простейшие движения твердого тела..............................38
- •Глава 8. Сложное движение.......................................................................45
- •Глава 9. Движение несвободной материальной точки............50
- •Глава 10. Работа и мощность....................................................................53
- •Глава 11. Общие теоремы динамики.....................................................61
- •Раздел 2.
- •Глава 18. Механические свойства конструкционных материалов......................................................................................................98
- •Глава 19. Расчет несущей способности типовых элементов, моделируемых в форме стержня...........................101
- •Глава 20. Устойчивость сжатых элементов конструкций...115
- •Раздел 4.
- •Глава 21. Зубчатые передачи...................................................................119
- •Глава 22. Червячные передачи................................................................127
- •Глава 23. Ременные передачи..................................................................132
- •Глава 24. Цепные передачи.......................................................................140
- •Глава 25.Несущие детали и опорные устройства механизмов......................................................................................142
- •Глава 26. Соединения деталей и узлов машин.......................152
- •Предисловие
- •Раздел 1. Основы расчета абсолютного твердого тела как модели механического объекта
- •Глава 1. Основные положения статики
- •1.1. Общие сведения
- •1.2. Аксиомы статики
- •1.3. Связи и их реакции
- •Глава 2. Плоская система сходящихся сил
- •2.1. Сложение плоской системы сходящихся сил. Геометрическое условие равновесия
- •2.2. Определение равнодействующей системы сходящихся сил методом проекций. Аналитическое условие равновесия
- •Глава 3. Теория пар сил на плоскости
- •3.1. Пара сил. Эквивалентность пар сил
- •3.2. Сложение пар сил. Условие равновесия пар
- •3.3. Момент пары относительно точки
- •Глава 4. Плоская система произвольно расположенных сил (пспрс)
- •4.1. Приведение силы к точке
- •4.2. Приведение к точке плоской системы произвольно расположенных сил
- •4.3. Теорема Вариньона
- •4.4. Уравнения равновесия и их различные формы
- •4.5. Балочные системы. Разновидности опор и виды нагрузок
- •2. Равномерно распределены.
- •4.6. Реальные связи. Трение скольжения и его законы
- •Основные законы трения
- •Глава 5. Пространственная система сил
- •5.1. Сложение пространственной системы сходящихся сил. Условие равновесия
- •5.2. Момент силы относительно оси
- •5.3. Пространственная система произвольно расположенных сил. Условие равновесия
- •Глава 6. Кинематика точки
- •6.1. Основные понятия кинематики
- •6.2. Способы задания движения точки
- •6.3. Определение скорости точки при естественном способе задания ее движения
- •6.4. Определение ускорения точки при естественном способе задания ее движения
- •6.5. Частные случаи движения точки
- •Равномерное движение точки по окружности
- •Глава 7. Простейшие движения твердого тела
- •7.1. Поступательное движение
- •7.2. Вращательное движение. Угловая скорость, угловое ускорение
- •7.3. Частные случаи вращательного движения
- •7.4. Скорости и ускорения различных точек вращающегося тела
- •7.5. Способы передачи вращательного движения
- •Глава 8. Сложное движение
- •8.1. Сложное движение точки
- •8.2. Плоскопараллельное движение тела
- •8.3. Определение скорости любой точки тела при плоскопараллельном движении
- •Глава 9. Движение несвободной материальной точки
- •9.1. Основные понятия и аксиомы динамики
- •9.2. Свободная и несвободная точки
- •9.3. Силы инерции
- •9.4. Принцип Даламбера
- •Глава 10. Работа и мощность
- •10.1. Работа постоянной силы на прямолинейном перемещении
- •10.2. Работа равнодействующей силы
- •10.3. Работа переменной силы на криволинейном пути
- •10.4. Мощность
- •10.5. Механический коэффициент полезного действия
- •10.6. Работа сил на наклонной плоскости
- •10.7. Работа и мощность при вращательном движении тел
- •10.8. Трение качения. Работа при качении тел
- •Глава 11. Общие теоремы динамики
- •11.1. Импульс силы. Количество движения. Кинетическая энергия
- •11.2. Теорема об изменении количества движения точки
- •11.3. Теорема об изменении кинетической энергии точки
- •11.4. Понятие о механической системе
- •11.5. Основное уравнение динамики вращающегося тела
- •11.6. Кинетическая энергия тела. Кинетический момент
- •Раздел 2. Основы построения и исследования механизмов
- •Глава 12. Структура механизмов
- •12.1. Основные понятия
- •12.2. Классификация кинематических пар. Кинематические цепи
- •Кинематические цепи
- •12.3. Структурный синтез и анализ механизмов
- •12.4. Конструктивно-функциональная классификация механизмов
- •12.5. Передаточное отношение
- •Глава 13. Основы расчета и проектирования механизмов
- •13.1. Общие сведения о передачах. Основные виды зубчатых передач
- •13.2. Общие сведения о методах изготовления зубчатых колес
- •13.3. Кинематика зубчатых механизмов с неподвижными осями вращения
- •13.4. Кинематика зубчатых механизмов с подвижными осями вращения
- •Глава 14.Основы кинематического анализа механизмов
- •14.1. Задачи и методы кинематического анализа механизмов. Масштабные коэффициенты
- •Масштабные коэффициенты
- •14.2. Построение положений рычажных механизмов методом засечек
- •14.3. Определение скоростей и ускорений рычажных механизмов методом планов
- •Глава 15. Методические указания к решению задач
- •15.1. Кинематика зубчатых механизмов с неподвижными осями вращения
- •15.2. Кинематика зубчатых механизмов с подвижными осями вращения
- •Раздел 3. Основы расчетов элементов конструкций
- •Глава 16. Напряженно-деформированное сечение детали
- •16.1. Метод сечений
- •16.2. Напряжение как мера внутренних сил
- •Глава 17. Напряженно-деформированное состояние элементарного объема материала
- •17.1. Напряженное состояние в точке. Закон парности касательных напряжений. Главные площадки и главные напряжения. Классификация напряженных состояний.
- •17.2. Однородное растяжение бруса как пример реализации одноосного напряженного состояния материала.
- •17.3. Продольная и поперечная деформации. Закон Гука. Модуль упругости. Коэффициент Пуассона
- •17.4. Частный случай плоского напряженного состояния – чистый сдвиг. Закон Гука при сдвиге.
- •Глава 18. Механические свойства конструкционных материалов
- •18.1. Экспериментальные исследования механических свойств при проведении стандартных испытаний на растяжении
- •18.2. Условие прочности, коэффициент запаса прочности, допускаемые напряжения.
- •Глава 19. Расчет несущей способности типовых элементов, моделируемых в форме стержня
- •19.1. Расчеты на прочность стержней при растяжении-сжатии.
- •19.2.Особенности расчета статически неопределимых стержневых систем
- •19.3. Напряженно-деформированное состояние при прямом поперечном изгибе.
- •19.4. Условия прочности при прямом поперечном изгибе.
- •19.5. Расчеты на жесткость при изгибе.
- •19.6. Кручение вала (стержня) круглого поперечного сечения.
- •19.7. Расчеты на прочность и жесткость при кручении.
- •19.8. Условие прочности вала при совместном действии крутящего и изгибающего моментов.
- •Глава 20. Устойчивость сжатых элементов Конструкций
- •20.1. Понятие о критической силе для сжатого стержня. Формула Эйлера.
- •20.2. Критическое напряжение. Пределы применимости формулы Эйлера.
- •Раздел 4. Расчет и конструирование деталей машин общего назначения и деталей отрасли
- •Глава 21. Зубчатые передачи
- •21.1. Геометрический расчет эвольвентных прямозубых передач
- •21.2. Особенности геометрии косозубых, шевронных и конических передач
- •21.3. Особенности геометрии конических колес
- •21.4. Усилия в зацеплении зубчатых передач
- •21.5. Материалы, термообработка для зубчатых колес
- •21.6. Расчеты зубьев на сопротивление усталости по изгибным и контактным напряжениям
- •1. Расчет зубьев на прочность при изгибе
- •Глава 22. Червячные передачи
- •2.1. Общие сведения. Геометрические и кинематические особенности червячных передач
- •22.2. Усилия в зацеплении. Расчет зубьев колес. Тепловой расчет червячных передач
- •Глава 23. Ременные передачи
- •23.1. Общие сведения. Ремни. Шкивы
- •23.2. Скольжение ремня.
- •23.3. Усилия и напряжения в ремнях. Тяговая способность и кпд передачи
- •Глава 24. Цепные передачи
- •24.1. Общие сведения. Цепи. Материалы
- •24.2. Усилия в элементах передачи. Расчет передачи
- •Глава 25. Несущие детали и опорше устройства механизмов
- •25.1. Валы и оси. Классификация. Расчет на прочность. Материалы
- •25.2. Опоры валов и осей. Классификация подшипников
- •25.3. Динамическая грузоподъемность подшипников качения. Выбор подшипников и определение их ресурса
- •25.4. Муфты механических приводов. Общие сведения и классификация
- •25.5. Муфты общего назначения. Особенности расчета
- •25.6. Предохранительные муфты
- •Глава 26. Соединения деталей и уздов машин
- •26.1. Сварные соединения. Общие сведения и характеристика. Изображения и обозначения на чертежах швов сварных соединений
- •26.2. Расчет на прочность и проектирование сварных соединений при постоянных нагрузках
- •26.3. Соединения пайкой и склеиванием
- •26.4. Соединения типа "вал - ступица": шпоночные, шлицевые, штифтовые. Общая характеристика и особенности расчета
- •26.4.1. Шпоночные соединения
- •26.4.2. Шлицевые соединения
- •26.4.3. Профильные соединения
- •26.4.4. Штифтовые соединения
- •26.5. Резьбовые соединения
- •26.5.1. Крепежные детали и стопорящие устройства
- •26.5.2. Резьба и ее параметры
- •26.5.3. Силовые зависимости в резьбовом соединении
- •26.5.4. Самоторможение и коэффициент полезного действия винтовой пары
- •26.5.5. Расчет резьбовых соединений на прочность
- •26.5.6. Расчет резьбовых соединений при переменном режиме нагружения
- •Литература
- •Приложения
- •Сортамент прокатной стали
- •Сталь горячекатаная. Швеллер. Гост 8240 – 89
- •Сталь горячекатаная. Уголки равнополочные. Гост 8509 – 86
- •Сталь горячекатаная. Уголки неравнополочные. Гост 8510 – 86
8.2. Плоскопараллельное движение тела
Движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости, называется плоскопараллельным.
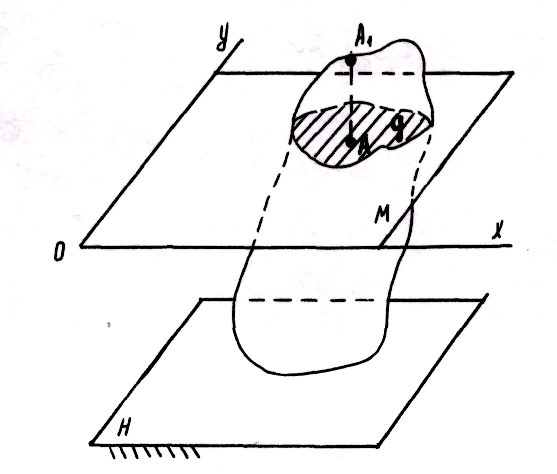
Изучая плоскопараллельное движение тела М, достаточно рассматривать движение его плоского сечения q плоскости ХОУ.
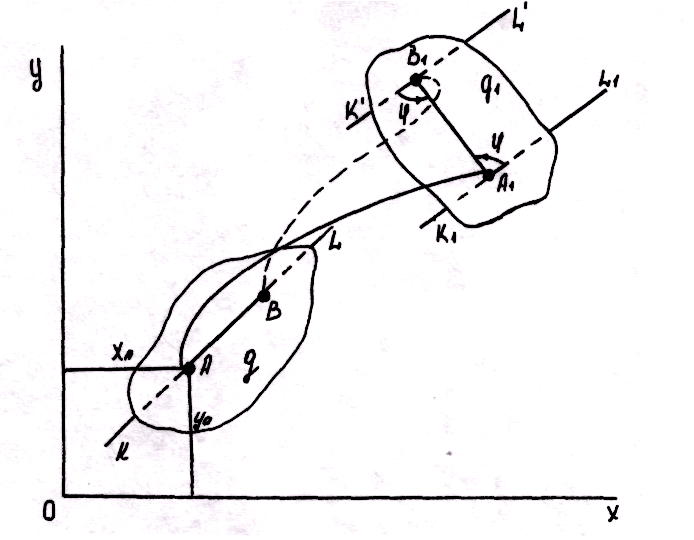
Выберем
в сечении q
произвольную
точку A,
которую назовем полюсом. Свяжем с полюсом
А некоторую прямую KL
, а в самом сечении вдоль прямой KL
проведем отрезок AB,
перемещая плоское сечение из положения
q
в положение q1.
Можно сначала передвинуть его вместе
с полюсом А поступательно, а затем
повернуть на угол ![]() .
.
Плоскопараллельное движение тела – движение сложное и состоит из поступательного движения вместе с полюсом и вращательного движения вокруг полюса.
Закон плоскопараллельного движения можно задать тремя уравнениями:
![]() .
.
Дифференцируя
заданные уравнения плоскопараллельного
движения, можно в каждый момент
времени определить скорость ![]() и
ускорение
и
ускорение ![]() полюса, а также угловую скорость
полюса, а также угловую скорость ![]() и угловое ускорение
и угловое ускорение ![]() тела.
тела.
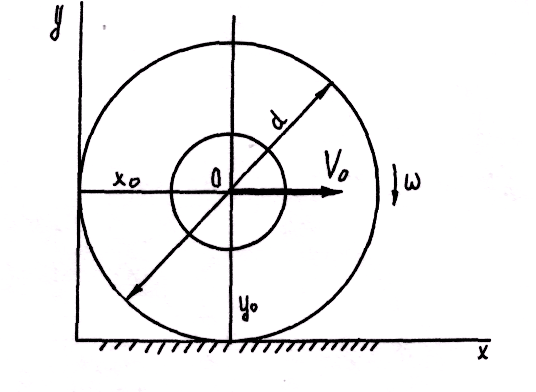
Пусть,
например, движение катящегося колеса
диаметром d
задано уравнениями ![]() ,
где
,
где ![]() и
и ![]() – м,
– м, ![]() – рад, t
– с. Продифференцировав эти уравнения,
находим, что скорость полюса O
– рад, t
– с. Продифференцировав эти уравнения,
находим, что скорость полюса O
![]() ,
угловая скорость колеса
,
угловая скорость колеса ![]() .
Ускорение полюса и угловое ускорение
колеса в данном случае равны нулю. Зная
скорость полюса и угловую скорость
тела, можно затем определить скорость
любой его точки.
.
Ускорение полюса и угловое ускорение
колеса в данном случае равны нулю. Зная
скорость полюса и угловую скорость
тела, можно затем определить скорость
любой его точки.
8.3. Определение скорости любой точки тела при плоскопараллельном движении
Пусть
дано плоское сечение q
, угловая скорость и скорость полюса
которого в некоторый момент времени
соответственно
![]() и
и
![]() .Требуется
определить скорость какой-либо точки
А.
.Требуется
определить скорость какой-либо точки
А.

Расчленим
плоскопараллельное движение на составные
части – поступательную и вращательную.
При поступательном движении вместе
с полюсом (переносное движение) все
точки сечения, и точка А в том числе,
имеют переносную скорость
![]() ,
равную скорости полюса. Одновременно
с поступательным сечениеq,
совершает
вращательное движение с угловой
скоростью
,
равную скорости полюса. Одновременно
с поступательным сечениеq,
совершает
вращательное движение с угловой
скоростью
![]() (относительное движение).
(относительное движение).
![]() ,
,
![]() – относительная
скорость точки A
(
– относительная
скорость точки A
(![]() ).
).
Следовательно, в каждый данный момент времени
![]() ,
,
т.е. абсолютная скорость точки тела при плоскопараллельном движении равна геометрической сумме скорости полюса и относительной скорости этой точки вокруг полюса.
Модуль абсолютной скорости может быть определен по формуле
![]() ,
,
а направление – с помощью теоремы синусов. Если же направление абсолютной скорости известно, то ее модуль определяется проще на основании следующей теоремы: проекции скоростей двух точек твердого тела на прямую, соединяющую эти точки, равны между собой.
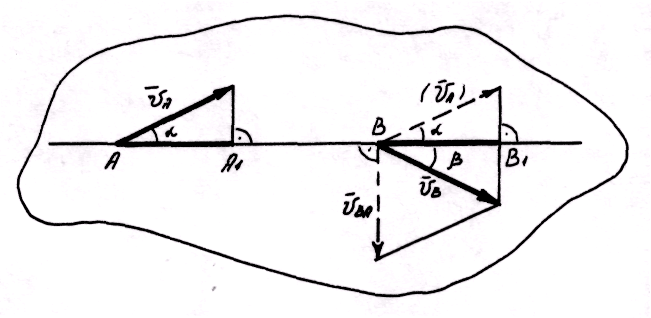
Допустим,
что известны скорости
![]() и
и
![]() точек A
и В какого-либо тела. Приняв за полюс
точку A,
получим
точек A
и В какого-либо тела. Приняв за полюс
точку A,
получим
![]() .
.
Относительная
скорость
![]() перпендикулярна
АВ. Следовательно,
перпендикулярна
АВ. Следовательно,
![]() или
или
![]() .
Теорема доказана.
.
Теорема доказана.
Глава 9. Движение несвободной материальной точки
9.1. Основные понятия и аксиомы динамики
Динамика изучает движение материальных тел под действием сил.
В основе динамики лежат следующие аксиомы.
Аксиома 1 (принцип инерции). Всякая изолированная материальная точка находится в состоянии покоя или равномерного и прямолинейного движения, пока приложенные силы не выведут ее из этого состояния.
Аксиома 2 (основной закон динамики). Ускорение материальной точки пропорционально действующей силе F и направлено по той прямой, по которой действует эта сила.
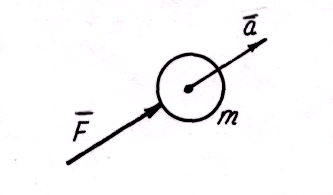
Математически вторая аксиома записывается векторным равенством
![]() ,
,
где коэффициент пропорциональности m выражает меру инертности материальной точки и называется ее массой. В Международной системе единиц (СИ) масса выражается в килограммах.
Зависимость между числовыми значениями (модулями) сил и ускорения выражается равенством
![]() .
.
На все материальные тела вблизи Земли действует сила тяжести G. При свободном падении на Землю тела любой массы приобретают одно и то же ускорение g, которое называется ускорением свободного падения. Для свободно падающего тела из предыдущего уравнения следует зависимость
![]() .
.
Таким образом, значение силы тяжести тела в ньютонах равно произведению его массы на ускорение свободного падения.
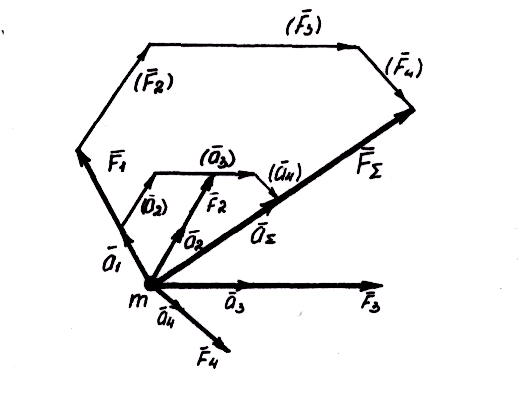
Аксиома 3 (закон независимости действия сил). Если к материальной точке приложена система сил, то каждая из сил системы сообщает точке такое же ускорение, какое она сообщила бы, действуя одна.
Таким
образом, при одновременном действии на
материальную точку массой m,
например, четырех сил, ускорение ![]() ,
полученное точкой, можно
,
полученное точкой, можно
определить,
геометрически сложив ускорения ![]() и
и ![]() ,
возникающие под действием каждой силы
в отдельности. В то же время ускорение
,
возникающие под действием каждой силы
в отдельности. В то же время ускорение
![]() пропорционально
равнодействующей
пропорционально
равнодействующей ![]() тех
же сил
тех
же сил![]() ,
,
где
![]() и
и
![]() .
.
Аксиома 4. Две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны.
