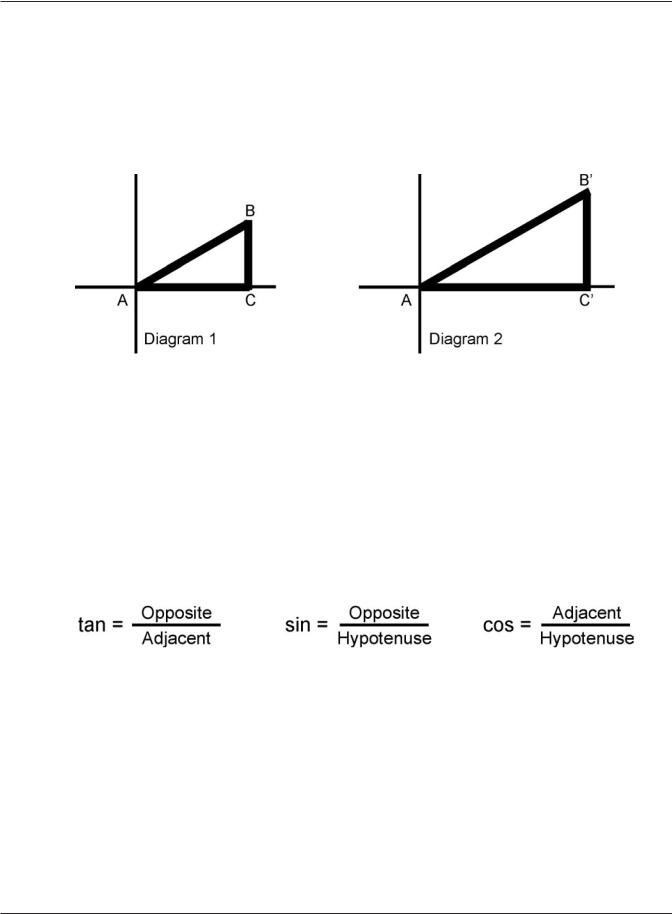
Appendix B

Trigonometric Relationships: Tangent, Sine, and Cosine

Consider a triangle ABC such that AB forms the hypotenuse, AC lies along the x-axis, and CB represents the y-axis height, as shown in Figure B.1, Diagram 1 on the left, below.

Figure B.1: Trigonometric Relationships In Right Triangles

In Figure B.1 Diagram 2 (above) the BC line has moved to the right (represented now as Bʼand Cʼ). There is an immutable ratio between the length of AC and the length of BC. As AC gets longer, BC gets taller, but always in a fixed ratio; a ratio based on the size of the angle at A. The ratio between the x-axis value and the y-axis value (AC and BC) is called the tangent of angle A. The basic trigonometric relationship is that the tangent value is equal to the ratio of the length of the side opposite the angle (BC) divided by the length of the side adjacent to the angle (AC). This gives rise to two additional relationships that are the sine and cosine ratios. The sine is the ratio of the length of the side opposite the angle (BC) divided by the length of the hypotenuse (AB). Cosine is the ratio of the length of the side adjacent the angle (AC) divided by the length of the hypotenuse (AB). These relationships are summarized in Figure B.2 below.

Figure B.2: The Basic Trigonometric Relationships in a Right Triangle

Copyright 2003 - Joseph Bardwell