FM_MMMFP (1) / ммфп мой (даты на рис)

МИНОБРНАУКИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «ВГТУ», ВГТУ)

Физико-технический факультет

Кафедра высшей математики и физико-математического моделирования

КУРСОВАЯ РАБОТА

по дисциплине «Математические методы моделирования физических процессов»

Тема: Математическое моделирование задач диффузии и теплопроводности методом конечных элементов.

Выполнила студентка ТФ - 091 Е.О.Буловацкая

группа подпись инициалы, фамилия

Руководитель И.Л. Батаронов

подпись инициалы, фамилия

Нормоконтроль И.Л. Батаронов

подпись инициалы, фамилия

Защищена________________ Оценка_____________________

Воронеж

2011

Воронежский государственный технический университет Кафедра высшей математики и физико-математического моделирования

ЗАДАНИЕ

на курсовую работу по дисциплине «Математические методы моделирования физических процессов»

студентке гр. ТФ-091 Буловацкой Е.О.

Специальность: «Техническая физика»

Тема работы: Математическое моделирование задач диффузии и теплопроводности методом конечных элементов.

Содержание расчётно-пояснительной записки:

Решение задач в декартовой и цилиндрической системе координат методом конечных элементов с помощью Flexpde:

1. Один конец тонкого изолированного стержня поддерживается при температуре равной нулю, а второй меняется по закону Аsinωt. Найти распределение температуры в стержне, если начальная температура равна нулю..

2. Найти установившееся распределение концентраций вокруг сферы, если плотность потока диффузанта через неё описывается выражением . Нарисовать следы концентрационных поверхностей..

Дата выдачи задания:

Дата сдачи курсовой работы:

Дата защиты курсовой работы:

Руководитель работы: И. Л. Батаронов

Исполнитель: Е.О.Буловацкая

Содержание

	Задание	2
	Введение	4
	Решение задачи № 1	7
	Решение задачи № 2	12
	Заключение	19
	Список использованной литературы	20

Введение

Уравнение теплопроводности. Процесс передачи тепло­ты от более нагретых частей тела к менее наг­ре­тым связан с изменением температуры u в различных частях тела. Поэтому описание такого процесса в мак­ро­скопической теории в общем случае сводится к определению нестационарного температур­ного поля в теле.

Рассмотрим одномерный процесс передачи теплоты тепло­проводностью в плоском слое изотропного материала (рис.1), считая, что температура u = u(х, t) является функцией лишь одного пространственного переменного х.

Плотность р материала, его удельную массовую теп­лоем­кость с и коэффициент теплопроводно­сти k в общем слу­чае неоднород­ной среды будем считать также зави­ся­щи­ми только от одной прос­транственной координаты х.

При построении математиче­ской модели процесса будем пред­полагать, что среда неподвижна, а изменение объема материала, связанное с изменением темпера­туры, пренебре­жи­мо мало. В этом случае можно считать, что про­цесс теплопро­водности не связан с совершением механи­ческой ра­боты.

В рассматриваемом слое материала в качестве некоторой термодинамической системы выделим объем V в виде цилиндра с площадью основания ΔS и осью, параллельной координатной оси Ох (см. рис. 1).

Из первого закона термодинамики, записанного для выде­ленного объема V, следует, что

(1)

где U - внутренняя энергия системы, которая может быть най­дена интегрированием объемной плотности внутренней энергии ε(х, t) по объему цилиндра, т.е.

Поэтому изменение внутренней энергии системы за единицу времени

(2)

Коли­чество теплоты Q₁, отдаваемое через поверхность за единицу времени, можно найти, инте­грируя по поверхности Σ нормальную составляющую плотности теплового потока . Поэтому

где - единичная внешняя нормаль к Σ.

Согласно физическому закону Фурье, при передаче тепло­ты теплопроводностью . Так как в рассматрива­емом случае вектор плотности теплового потока имеет лишь одну составляющую , то тепловой поток от выделенного объема проходит лишь через основания цилиндра, причем

(3)

Внутри выделенного объема вследствие протекания эндо- или экзотермических реакций, про­хож­дения электрического тока, испарения влаги в пористом материале и других при­чин может выделяться или поглощаться теплота. Если под F(х, t) пони­мать объемную плот­ность (удельную мощность) тепловых ис­точников, то за единицу времени в рассмат­ри­ваемом объеме выделится (F > 0) или поглотится (F < 0) количество теплоты

(4)

Подставив выражения (2) - (4) в уравнение (1), получим

(5)

В силу произвольности выбора координат х₁ и x₂ основа­ний цилиндра равенство нулю интеграла в уравнении (5) воз­можно лишь при равенстве нулю подынтегральной функции.

Таким образом, в каждой точке пространства, должно выполнять­ся следующее дифференциальное соотношение:

(6)

Заметим, что объемная плотность внутренней энергии рас­сматриваемой несжи­мае­мой среды ε = ε (и) зависит от температуры, а производная , определяет объемную теп­лоем­кость материала. Поэтому

Тогда из выражения (6) получаем дифференциальное уравне­ние

(7)

Для однородного материала с независящими от температу­ры теплофизическими ха­рак­теристиками ρ, с и k уравнение (7) можно записать в виде

(8)

где a² = k/(ρс) - постоянная, которую называют коэффициен­том температуропроводности мате­риала; .

Уравнения (7) и (8) являются дифференциальными урав­нениями в частных произ­вод­ных параболического типа. Они лежат в основе математических моделей, описы­ваю­щих процесс передачи теплоты в неоднородных и однородных телах с одно­мерным темпе­ра­турным полем. Эти уравнения называются уравнениями теплопроводности.

Решение задачи № 1.

Один конец тонкого изолированного стержня поддерживается при температуре равной нулю, а второй меняется по закону Аsinωt. Найти распределение температуры в стержне, если начальная температура равна нулю.

Для решения задачи будем использовать специальное приложение FlexPDE 6.20.

Предположим, что коэффициент теплопроводности K = 2 Вт/(м*К), длина стержня L=5 м, частота W = 5 Гц, а амплитуда колебаний А=1м.

TITLE

'New Problem'

COORDINATES

cartesian1

VARIABLES

u(threshold=100)

DEFINITIONS

K=2

cp=1

L=5

w=5

A=1

EQUATIONS

div(K*grad(u))=cp*dt(u)

BOUNDARIES

REGION 1

start(0) point value(u) = 0

line to (0+L) point value(u) = A*sin(w*t)

TIME 0 TO 10 by 0.01

MONITORS

for t = 0.0 by 0.1 to (0+L)

elevation(u) from (0) to (0+L) range=(0,1) as "Surface Temp"

plots

elevation(-k*grad(u)) from(0) to (0+L)

histories

history(u) at (5)(6)(7)

END

Рисунок1. Распределение температуры в начальный момент времени

Рисунок 3. Направления потока температуры

Рисунок 4. Изменение поля во времени в отдельных точках

При увеличении коэффициент теплопроводности в 2 раза (K = 2 Вт/(м*К)) картина меняется.

Рисунок 5. Распределение температуры в начальный момент времени

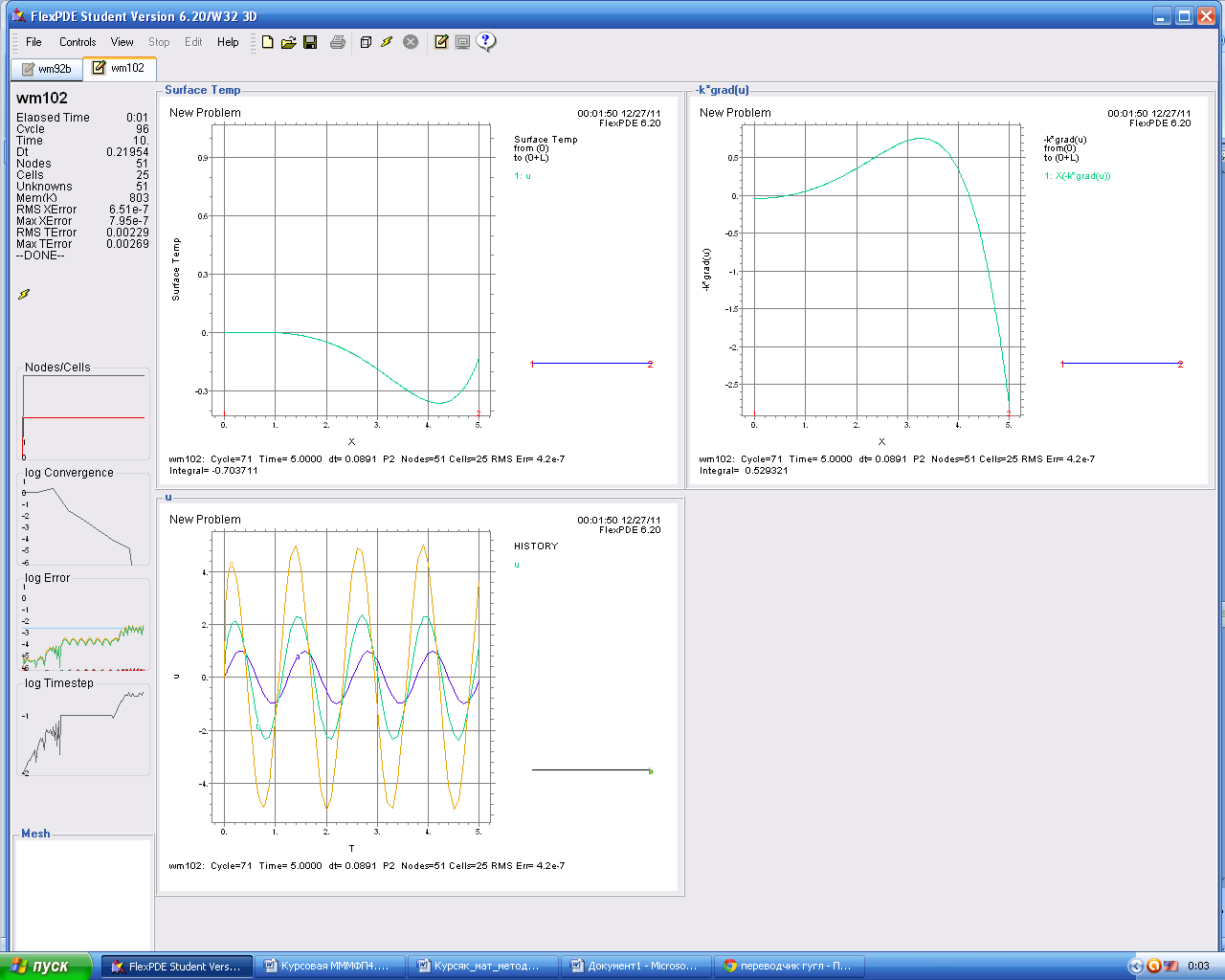
Рисунок 6. Направления потока температуры

Рисунок 7. Изменение поля во времени в отдельных точках

Решение задачи № 2.

Найти установившееся распределение концентраций вокруг сферы, если плотность потока диффузанта через неё описывается выражением . Нарисовать следы концентрационных поверхностей.

В нашей задаче объемная плотность источника диффузанта равна нулю, т.к. объёмных источников нет. Поэтому уравнение будет иметь вид: div(grad(N)) = 0.

_{Для задания условия на границе сферы необходимо выразить} через координаты R и Z. Получим, что

Для решения задачи будем использовать специальное приложение FlexPDE 6.20

TITLE

'New Problem'

COORDINATES

ycylinder ('R','Z')

VARIABLES

u

DEFINITIONS

R0=1.2

k=0.5

A=10

EQUATIONS

div(k*grad(u))=0

BOUNDARIES

REGION 1

START(0,-R0)

natural (u)=0

arc(center=0,0)to (R0,0)

natural(u)=0

arc(center=0,0)to (0,R0)

natural(u)=0

LINE TO (0,1)

value(u)=A*Z/SQRT(R^2+Z^2)

arc(center=0,0) to (1,0)

value(u)=A*Z/SQRT(R^2+Z^2)

arc(center=0,0) to (0,-1)

natural(u)=0

line TO CLOSE

MONITORS

contour(u)

PLOTS

CONTOUR(u)

surface(u)

vector(k*grad(u))

END

Рисунок8 Распределение концентрации

Рисунок 9. Поверхность распределения концентрации

Рисунок 10. Направления потока концентрации

Увеличим RO в 2 раза и получим следующие результаты

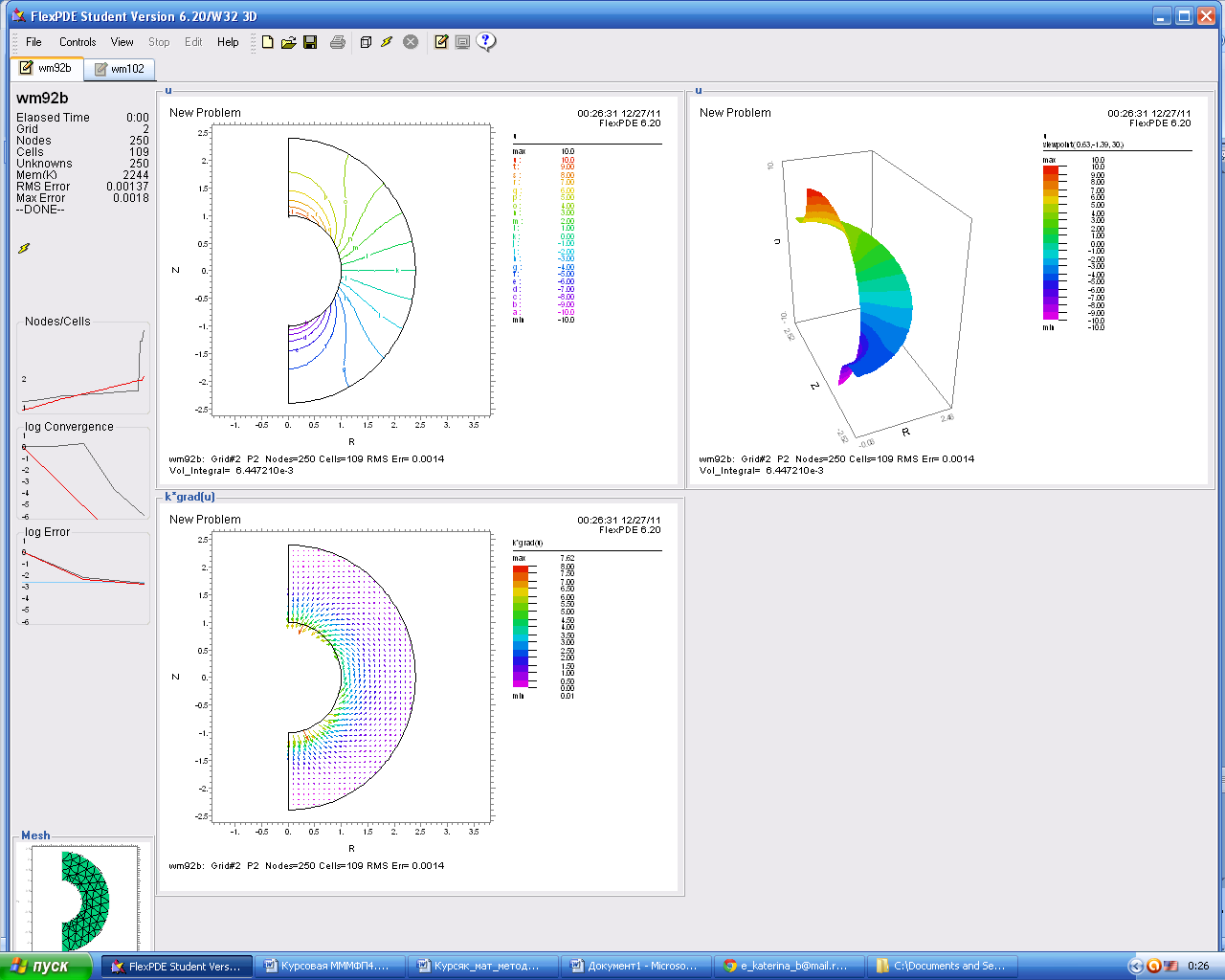
Рисунок 11 Распределение концентрации

Рисунок 12. Поверхность распределения концентрации

Рисунок 13. Направления потока концентрации

Увеличим R0 еще в 2 раза и получим:

Рисунок 11 Распределение концентрации

Рисунок 12. Поверхность распределения концентрации

Рисунок 13. Направления потока концентрации

Заключение.

В данной работе мы моделировали уравнения диффузии и теплопроводности с помощью приложения FlexPDE. В задаче теплопроводности решалось уравнение параболического типа, и в итоге были получены графики распределения температур в тонком изолированном стержне, в котором один конец поддерживается при температуре Т=0, а температура второго меняется по закону Аsin(ωt).

Во второй задаче решалось эллиптическое уравнение диффузии с поверхности сферы. В итоге была получена картина установившегося распределения диффузанта и следы концентрационных поверхностей.

Список используемой литературы

1. Мартинсон Л. К., Малов Ю. И. Дифференциальные уравнения математической физики. – 3-е изд., испр. – М.: Издательство МГТУ имени Баумана, 2006 – 60 с.