KR_No3

Проинтегрировав это выражение, найдем

t= c r(1/T23 – 1/T13)/ 3 . (6)

После подстановки числовых значений получим t = 500 с.

Пример 2. Вследствие изменения температуры черного тела максимум спектральной плотности энергетической светимости сместился с длины волны 1 =2,4 мкм на2=0,8 мкм. Как и во сколько раз изменилась энергетическая светимость тела и максимальная спектральная плотность энергетической светимости?

Решение

Зная длины волн, на которые приходятся максимумы лучеиспускательной способности тела, и, используя закон смещения Вина, находим начальную и конечную температуры тела

T1= b/ 1, T2= b/ 2 .

Энергетическая светимость черного тела определяется согласно закону Стефана-Больцмана

R*= T4 ,

следовательно, R1*/ R2* = (T2/T1)4 = ( 1/ 2)4 .

Максимальное значение спектральной плотности энергетической светимости определяется по второму закону Вина

Подставляя числовые значения, получаем

R2*/R1* = 81;

r*2max/ r*1max = 243.

Пример 3. Красная граница фотоэффекта у рубидия равна0=0,8 мкм. Определить максимальную скорость фотоэлектронов при облучении рубидия монохроматическим светом с длиной волны =0,4 мкм. Какую задерживающую

19

разность потенциалов нужно приложить к фотоэлементу, чтобы прекратился ток?

Решение

Энергия фотона вычисляется по формуле =hc/ и составляет для =0,4 мкм = 3,1эВ. Эта величина значительно меньше энергии покоя электрона, поэтому максимальная кинетическая энергия фотоэлектрона может быть выражена классической формулой Tmax = ½ mVmax2. Выразив работу выхода через красную границу фотоэффекта, на основании

уравнения Эйнштейна получим

Tmax= ½ m Vmax2 = h c/ - h c/ 0 .

Откуда

Vmax= (2 h c( 0 - )/(m 0 ))1/2 .

Подставив числовые значения, найдем Vmax = 0,74 108 м/с. При U<0 внешнее поле между катодом и анодом

фотоэлемента тормозит движение электронов. Задерживающая разность потенциалов Uз, при которой сила тока обращается в нуль, определится из уравнения e Uз = m Vmax2 /2.

Следовательно, Uз= hc(1/ - 1/ 0) /e = 1,58 В.

Пример 4. Уединенный медный шарик облучают ультрафиолетовыми излучением с длиной волны =165 нм. До какого максимального потенциала зарядится шарик?

Решение

Вследствие вылета электронов под действием излучения шарик заряжается положительно. Электрическое поле шарика тормозит вылетевшие электроны, однако, если их кинетическая энергия достаточно велика для преодоления электростатического притяжения, то они будут уходить практически в бесконечность. Максимальный потенциал, до которого зарядится шарик, определится из выражения

e max= m Vmax2 /2.

20

Из уравнения Эйнштейна

m Vmax2 /2= h - A = hc/ - A ,

тогда

max= (hc/ - A) /e = 3 эВ.

Пример 5. Фотон испытал рассеяние на покоившемся свободном электроне. Найти импульс налетавшего фотона, если энергия рассеянного фотона равна кинетической энергии электрона отдачи при угле = /2 между направлениями их разлета.

Решение

Кинетическая энергия T электрона отдачи на основании закона сохранения энергии равна разности между энергией падающего фотона и энергией ’ рассеянного фотона

T= - ’ .

По условию задачи T= ’, значит, = 2 ’, или hc/ = 2hc/ ’ ,

откуда / ’= 0,5 , а с учетом формулы P= h/ , P’/P =0,5. Воспользуемся законом сохранения импульса, в соответствии с которым

21

Пример 6. Определить импульс электрона отдачи при эффекте Комптона, если фотон с энергией, равной энергии покоя электрона, был рассеян под угол = 180 .

Решение

Используя формулы для энергии и импульса фотона, определяем длину волны и импульс падающего фотона. Так как по условию

= hc/ =m0c2,

то

λ=h /m0 c , P= h / = m0 c.

В соответствии с формулой Комптона для данного случая

’ - = k (1 – cos180 ) = 2 k ,

откуда длина волны рассеянного фотона равна

’= 2 k + = 2h/ (m0 c) + h/ (m0 c) = 3h /(m0 c).

Величина его импульса

P’= h/ ’ = m0 c/ 3.

Для нахождения импульса электрона отдачи построим векторную диаграмму импульсов.

P = -P’ + mυ.

Из полученного уравнения найдем mυ= P + P’ = 4/3 m0c.

Подставив числовые значения, получим mυ= 3,64∙10-22 кг м/с.

Пример 7. Пучок монохроматического света с длиной волны λ = 663 нм падает нормально на зеркальную плоскую поверхность. Поток излучения Фе=0,6 Вт. Определить:

1)силу давления F, испытываемую этой поверхностью;

2)число фотонов ежесекундно падающих на поверхность.

22

Решение

1) Сила светового давления на поверхность равна произве-

где, Е0 – энергетическая освещённость; с – скорость света в вакууме; ρ - коэффициент отражения.

Подставляя правую часть уравнения (2) в формулу (1),

Проведём вычисления, учитывая, что для зеркальной поверхности ρ=1 :

0,6

F (1 1) 4 нН . 3 108

2) Произведение энергии ε одного фотона на число фотонов n1, ежесекундно падающих на поверхность, равно мощности излучения, т.е.потоку излучения: Фе= εn1, а так как

3.ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ

3.1.Основные законы и формулы

1.Формула де Бройля

= h/m.V

2.Соотношение неопределенностей Гейзенберга

x. px ; E. t ,

23

где h .

где - оператор Лапласа, E – полная энергия частицы,

U – потенциальная энергия частицы, - волновая функция. 4. Вероятность обнаружить частицу в объеме dV

dp = 2 . dV .

Условие нормировки волновой функции

2 dV 1.

5. Волновая функция, описывающая движение свободной частицы

(x,t) = A . e –i( E t – p x) / .

6.Собственные значения энергии и собственные волновые функции для частицы, находящейся в одномерной прямоугольной бесконечно глубокой потенциальной яме

(x) 2 d sin( nx), d

где d – ширина потенциальной ямы.

7. Коэффициент прозрачности прямоугольного потенциального барьера

2

D exp[ 2m(U 0 E)d ]

где d – ширина барьера, E – энергия частицы.

24

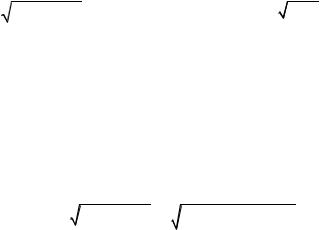
3.2. Примеры решения задач Пример 1. Поток моноэнергетических электронов падает

нормально на диафрагму с узкой щелью шириной b= 2мкм. Найти скорость электронов, если на экране, отстоящем от щели на L=50 см, ширина центрального дифракционного максимума x=0,36 мм.

Решение

Согласно гипотезе де Бройля длина волны , соответствующая частице массой m, движущейся со скоростью V, выражается формулой

Для минимумов первого порядка

(k=1), угол заведомо мал, поэтому sin = , и, следовательно, формула (2) примет вид

Пример 2. Определить длину волны де Бройля λ электрона, прошедшего ускоряющую разность потенциалов

700 кВ.

Решение

Связь длины волны де Бройля с импульсом

hp ,

где h = 6,63 10-34Дж с – постоянная Планка, причём импульс

где m, T, E0 – соответственно масса, кинетическая энергия, энергия покоя частицы.

Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U,

Т= e U = 0,7МэВ,

а энергия покоя электрона Е0 = mc2 = 0,5МэВ, т.е. в данном случае имеем дело с релятивистской частицей.

Тогда искомая длина волны де Бройля

где m = 9,11 10-31кг; c =3 108м/c; е =1,6 10-19Кл.

Вичисляя, получаем λ= 1,13пм.

Пример 3. Используя соотношения неопределенностейx px h/2 , найти выражение, позволяющее оценить минимальную энергию E электрона, находящегося в одномерном потенциальном ящике шириной l.

Решение

Из данного соотношения следует, что, чем точнее определяется положение частицы, тем более неопределенным становится импульс, а, следовательно, и энергия частицы. Неопределенность координаты электрона x=l/2. Тогда соотношение неопределенностей можно записать в виде

26

l /2 p h/2 ,

откуда

p h/ l.

Физически разумная неопределенность импульса p, во всяком случае, не должна превышать значения самого импульса, т.е. p p.

Энергия E электрона, находящегося в одномерном потенциальном ящике, есть его кинетическая энергия T,

величину которой можно связать с импульсом соотношением

T= p2 / 2m .

Заменив p на p, получим

Emin= (h2/2 2)/(m l2)=2 2ml2 .

Пример 4. Электрон находится в бесконечно глубокой одномерной прямоугольной потенциальной яме шириной L. Вычислить вероятность обнаружения электрона на первом энергетическом уровне в интервале L /4, равноудаленном от стенок ямы.

Решение

Вероятность P обнаружить частицу в интервале x1<x<x2 определяется равенством

где (x) – нормированная собственная волновая функция, отвечающая данному состоянию.

Нормированная собственная волновая функция, описывающая состояние электрона в потенциальной яме, имеет вид

n(x)= (2/L)½ sin( n x/L).

Невозбужденному состоянию (n=1) отвечает волновая функция

27

Подставив 1(x) в подынтегральное выражение формулы (1) и вынося постоянные за знак интеграла, получим

Согласно условию задачи x1=3L/8 и x2=5L/8. Произведя замену sin2( x/L) = 1 /2 [1 – cos(2 x/L)] ,

получим

4.ФИЗИКА АТОМОВ

4.1.Основные законы и формулы

1.Собственные значения энергии электрона в атоме водорода и водородоподобном ионе

где n = 1,2,3…- главное квантовое число; Z – порядковый номер элемента; h = 6.62∙10-34 Дж·с – постоянная Планка; R= 3,28∙1015с-1 – постоянная Ридберга.

2. Орбитальный механический момент импульса L электрона и его проекция на заданное направление z внешнего магнитного поля

где = 0,1,2…(n-1) – орбитальное квантовое число; где m = 0, 1, 2… - магнитное квантовое число;

h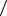2 1,05 10 34 Дж / с.

28