4. Теория многомерной полезности

Теория многомерной полезности позволяет для задач в условиях риска и неопределенности получить функцию многомерной полезности, максимальное значение которой соответствует наиболее предпочтительному варианту. Многомерная функция полезности обычно получается как аддитивная или мультипликативная комбинация одномерных функций, которые строятся на основании опроса экспертов и позволяют провести ранжирование возможных исходов без взаимного сравнения альтернатив. При этом делается допущение о взаимной независимости критериев по полезности. Процедура построения функции полезности требует привлечения значительных объемов информации и является достаточно трудоемкой. Достоинством этого подхода является возможность оценки любого количества альтернативных вариантов с использованием полученной функции. В случае неустойчивой исходной информации применение методов теории полезности становится малоэффективным.

В общем случае полезность каждого варианта зависит от его оценок по многим частным критериям. Необходимость учета этого обсто­ятельства привела к созданию аксиоматической теории много­мерной полезности (Multi-Attribute Utility Theory — MAUT), су­щественный вклад в построение которой внесли Р. Кини, Г. Рай- фа, П. Фишберн (США).

Теория опирается на формальные допущения (аксиомы), ха­рактеризующие предпочтения ЛПР и задающие определенный вид функции полезности. Предложены разные системы таких аксиом. Представим одну из наиболее известных аксиоматик многомерной полезности, которая включает в себя аксиомы, ана­логичные используемым в теории одномерной полезности, и ряд дополнительных аксиом, устанавливающих независимость пред­почтений ЛПР.

МП1. Аксиома полной сравнимости. При сравнении любых двух вариантоввыполняется одно и только одно бинар­ное отношение между полезностями вариантовли­бо равенство, либо строгий порядок или

МП2. Аксиома транзитивности. Отношения равенства и строгого порядка между полезностями вариантов транзитивны:

МП3. Аксиома растворимости. Для любых вариантов таких, чтонайдется такая вероят­ность р, что полезности вариантаи простой лотереи равны:

МП4. Аксиома Архимеда. Для любых вариантов таких, что|, найдутся вероятности р и q

такие, что полезности вариантаи простых лотерей удовлетворяют неравенствам

МП5. Аксиома независимости по предпочтению. Для лю­бых вариантовтаких, чтонайдется та­кая вероятность р, что полезности простых лотерейи при любом вариантеудовлетворяют неравенству

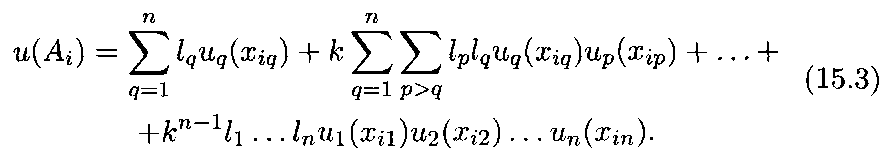
МП6. Аксиома независимости по полезности. Для любых простых лотерейтаких, что, найдется та­кая вероятность р, что полезности составных лотерей ипри любом вариантеудовлетворяют неравенству

Аксиомы МП1 и МП2 совпадают с аксиомами ОП1 и ОП2. Аксиомы МПЗ и МП4 в совокупности аналогичны аксиомам ОПЗ и ОП4. Аксиомы независимости по предпочтению МП5 и полезности МП6 означают, что на результаты сравнения двух конкретных вариантов или лотерей не влияет присутствие каких-либо третьих вариантов. На критериальном языке это зву­чит так: предпочтительность вариантов и лотерей, которые раз­личаются лишь значениями оценок по отдельным частным кри­териям, не зависит от одинаковых фиксированных значений оце­нок по остальным частным критериям.

Доказано, что при выполнении аксиом МП1 — МП6 существу­ет действительная многомерная функцияполезности, за­данная на множестве вариантовв виде поли­линейной функции

Здесь— полезность оценкивариантапо q-му частному критериюудовлетворяющая условию нормировки причемхудшая и лучшая оценка по шкале критериячаст­ный шкалирующий параметр, который определяется значением функции полезности Общая шкалирующая константанаходится из характе­ристического уравнения

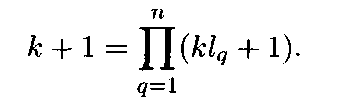
Прифункция полезностиприобретает адди­тивную форму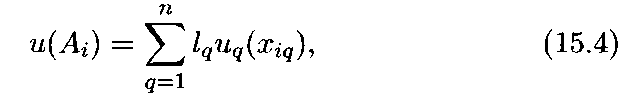а примультипликативную форму

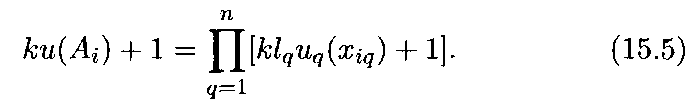
При к = 0 мультипликативная функция полезности (15.5) сводится к аддитивной функции (15.4). Как и в одномерном слу­чае, вариантпредпочтительнее для ЛПР вариантатогда и только тогда, когдаварианты экви­валентны для ЛПР

На практике нахождение численных значений шкалирующих константи конкретного выражения для функции многомер­ной полезности сопряжено со значительными трудностями. Это связано с большими расхождениями, которые может допускать ЛПР при выражении своих предпочтений.

Заключение

В данной курсовой работе мы рассмотрели системный анализ с точки зрения принятия решений, были подробно рассмотрены основные принципы системного анализа. Главной задачей было рассмотрение принятие решений в условиях неопределенности. Также рассмотрели основные критерии, используемые в процессе принятия решений в условиях неопределенности. Подробно рассмотрели критерий Гурвица, привели пример к данному критерию. Не мало важную роль в принятии решений играет теория многомерной полезности. В теории многомерной полезности рассмотрели общие положения.

Принятие решения — это процесс рационального или иррационального выбора альтернатив, имеющий целью достижение осознаваемого результата.