Биномиальное распределение, его математическое ожидание, дисперсия

Рассмотрим серию независимых испытаний проведенных в условиях схемы Бернулли, в ходе которых появлялось событиес вероятностью, одинаковой для всех испытаний.

Необходимо определить закон распределения случайной величины числа появлений события. Для этого нужно определить возможные значенияи их вероятности. Минимальное значениеравно нулю, что соответствует ситуации, когда в сериииспытаний событиене появилось; максимальное значениесоответствует «успеху» во всех испытаниях серии и равно. Очевидно, что случайная величиначисла появлений событияв сериииспытаний принимает значения. Остается найти соответствующие вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:

,

где ,.

Эта формула является аналитическим выражением искомого закона распределения. Эта формула еще называется биномиальной, так как ее правая часть представляет собой -й член бинома Ньютона:

.

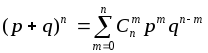Отсюда сразу видно, что для полученного закона биномиального распределения вероятностей числа появления события принезависимых испытаниях выполняется условие нормировки, т.е. сумма всех вероятностей равна единице:

.

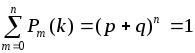Теорема. Математическое ожидание числа появлений события внезависимых испытаниях равно произведению числа испытаний на вероятность появления событияв каждом испытании.

Доказательство. Случайная величина распределена по биномиальному закону:

(),

где .

Величину можно рассматривать, как сумму независимых случайных величин, где() – число появлений событиявм испытании. Случайная величинапринимает лишь два значения: 1, если событиепоявилось вм испытании, и 0, если вм испытании событияне произошло.

Вероятности этих событий и, а математическое ожидание:().

Следовательно, используя теорему о математическом ожидании суммы, получим:

.

Таким образом, математическое ожидание числа появлений события в условиях схемы Бернулли совпадает со средним числом появлений событияв данной серии испытаний.

Теорема. Дисперсия числа появлений события внезависимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления событияв одном испытании:.

Доказательство. Пусть – число появлений событиявнезависимых испытаниях. Оно равно сумме появлений событияв каждом испытании:. Так как испытания независимы, то и случайные величины– независимы, поэтому.

Но ,.

Как было показано выше, , а.

Тогда , а.

В этом случае, как уже упоминалось ранее, среднее квадратичное отклонение .

Пример. В пяти торговых точках проверяется годовой баланс. Вероятность правильного оформления баланса в каждой точке равна 0,7. Найти математическое ожидание и дисперсию правильно оформленных балансов.

Решение. Дано: ,,.

Тогда

.

Биномиальный закон распределения часть приходится применять в условиях, когда число независимых испытаний велико. Вычисление вероятностей по формуле Бернулли при этом усложняется, поэтому представляет интерес асимптотическое приближение для биномиального закона, справедливое при больших . Возможны два случая:

1. Когда при увеличении числа испытаний математическое ожидание рассматриваемой случайной величины 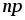тоже неограниченно возрастает (случай постоянного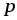); при этом биномиальное распределение сходится к нормальному закону, который будет рассмотрен позже.

2. Когда при увеличении числа испытаний остается постоянным произведение 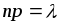, то есть математическое ожидание рассматриваемой случайной величины остается конечным. Это означает, что вероятность события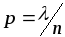стремится к нулю. В этом случае биномиальное распределение сходится к распределению Пуассона.

Распределение пуассона

Рассмотрим второй случай асимптотического приближения биномиального распределения, когда , а– имеет конечное значение. Случайная величинаназываетсяраспределенной по закону Пуассона с параметром , если эта случайная величина может принимать значения, соответствующая вероятность которых определяется по формуле Пуассона, когда:

.

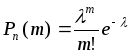В биномиальном распределении величина имеет смысл математического ожидания. Проведем вычисления математического ожидания для распределения Пуассона:

.

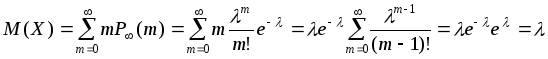Таким образом, в распределении Пуассона величина также имеет смысл математического ожидания.

Проведем вычисления дисперсии для распределения Пуассона:

,

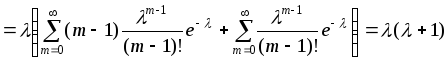поскольку

,

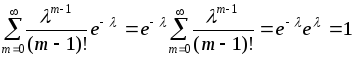
Таким образом, в распределении Пуассона дисперсия также равна .

Нормальное распределение

Нормальным называется такое распределение случайной величины , плотность вероятности которого описывается функцией Гаусса:

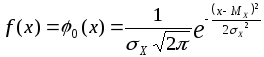
где – среднее квадратичное отклонение;

– математическое ожидание случайной величины.

Свойства функции Гаусса

График плотности нормального распределения называют нормальной кривой Гаусса.

Проведем исследование функции:

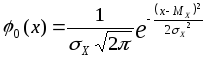
методами дифференциального исчисления.

1. Очевидно, что функция определена на всей оси .

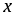2. При всех значениях 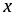функция принимает положительные значения, т.е. нормальная кривая расположена над осью.

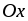3. Ось 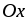служит горизонтальной асимптотой графика, поскольку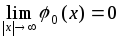. Других асимптот у графика нет.

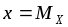4. При функция имеет максимум, равный.

5. Функция четная: ее график симметричен относительно прямой .

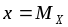6. При 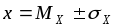график функции имеет точки перегиба.

Изменение величины математического ожидания, т.е. параметра , ведет к сдвигу кривой вдоль осибез изменения ее формы. График ведет себя иначе, если изменяется среднее квадратичное отклонение (параметр): с возрастаниеммаксимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси; при убываниинормальная кривая становится более островершинной и растягивается в положительном направлении оси. Нопри любых значениях параметров и, согласно условию нормировки функции плотности распределения, площадь, ограниченная нормальной кривой и осьюостается равной единице.

Схема независимых испытаний Бернулли

Серия повторных независимых испытаний, в каждом из которых данное событие имеет одну и ту же вероятность, не зависящую от номера испытания, называетсясхемой Бернулли. Таким образом, в схеме Бернулли для каждого испытания имеются только два исхода: событие (успех), вероятность которогои событие(неудача), вероятность которого.

Рассмотрим задачу: в условиях схемы Бернулли необходимо определить вероятность того, что при проведении независимых испытаний, виспытаниях наступит событие, если вероятность его наступления в каждом испытании равна.

Определим вначале вероятность того, что в первых испытаниях событиенаступит, а в остальныхиспытаниях не наступит. Вероятность такого события можно получить по формуле вероятности произведения независимых событий, где.

Это лишь одна из возможных комбинаций, когда событие произошло только в первыхиспытаниях. Для определения искомой вероятности нужно перебрать все возможные комбинации. Их число равно числу сочетаний изэлементов по, т.е..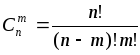

Таким образом, вероятность того, что событие наступит в любыхиспытаниях, определяется поформуле Бернулли:

.

Наивероятнейшее число наступления событий в схеме Бернулли

Число наступлений события называетсянаивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления любое другое количество раз.

Теорема. Наивероятнейшее число наступлений события внезависимых испытаниях заключено между числамии.

Доказательство. По формуле Бернулли при :

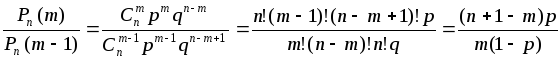
Следовательно, вероятность будет больше, меньше или равна вероятностив зависимости от того, какое из трех соотношений будет выполняться:

,

,

.

Если переписать эти соотношения в более простом виде:

,

,

,

То приходим к выводу, что:

, если ;

, если ;

, если .

Следовательно, вероятность привозрастает, а при– убывает. В случае, когдане является целым числом, для наивероятнейшего числа наступлений события(обозначим его) должно выполняться неравенство, что возможно при, т.е. при. В то же время, должно выполняться неравенство, что возможно при, т.е. при. Таким образом,.

Заметим, что разность между иравна единице, значит, в большинстве случаев числоединственно. Если– целое число, то наивероятнейших чиселдва:и. В этом случае, поскольку

, то, а.

Полиномиальная схема

Схему независимых испытаний Бернулли еще называют биномиальной схемой, поскольку она рассматривает последовательности испытаний с двумя исходами. От нее можно перейти к более общей полиномиальной схеме последовательных независимых испытаний, в каждом из которых возможны исходов с вероятностями,,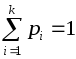. В этом случае пространство элементарных исходов содержиттаких событий. Вероятность того, что изиспытанийзакончатся первым исходом,– вторым исходом, …,–-ым исходом равна:

.
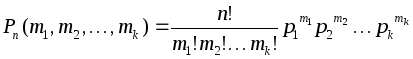
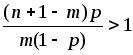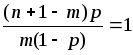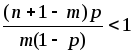