4 Задача №2.1

Найдите, воспользовавшись формулами Фурье, выражения для определения постоянной составляющей и амплитуд гармоник одного из процессов, представленных на рис.2.1, в соответствии с Вашим номером N.

Определите численно по найденным Вами выражениям постоянную составляющую и амплитуды восьми первых гармонических составляющих процесса. Представьте спектр амплитуд в графическом виде. Параметры сигнала примите равными: = 2( 15 + 2N ) рад/с, I = 8NG А.

Рис.2.1а.

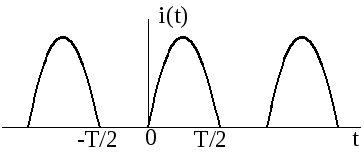
Рис.2.1б.

5

Рис.2.1в

Рис.2.1г

Рис. 2.1д

Рис.2.1е

6

Рис.2.1ж

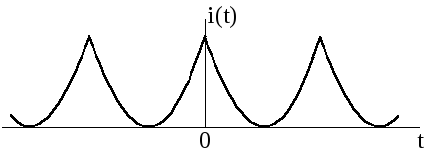
Рис.2.1и

КОНТРОЛЬНЫЕ ВОПРОСЫ

2.10. Почему нельзя описывать спектры непериодических сигналов с помощью ряда Фурье?

2.11 Запишите прямое и обратное преобразования Фурье. Как осуществляется переход от ряда Фурье к преобразованию Фурье?Каков физический смысл полной комплексной спектральной плотности?

2.12. Как определяя плотность амплитуд и спектр фаз непериодического сигнала, каков их физический смысл и размерность?

2.13. Опишите влияние симметрии сигнала на свойства полной комплексной спектральной плотности, спектров амплитуд и фаз.

2.14. Как определяется ширина спектра одиночного импульса? Как проводится инженерная оценка его ширины спектра?

7 Задача №2.2

Спектр импульса прямоугольной формы (рис.2.2,а), определяется комплексной спектральной плотностью

где - длительность импульса.

Модуль и аргумент спектральной плотности выражаются равенствами:

где - целое число.

Рис.2.2

Зависимости их значений от частоты приведены в графическом виде на рис.2.3.

8

Рис. 2.4.

Рис.2.3.

Первая кривая показывает, как зависит от частоты спектральная плотность а м п л и т у д , вторая - спектр ф а з импульса рис.2.2а. Воспользовавшись теоремой смещения, определите комплексную спектральную плотность импульса (рис.2.2б), сдвинутого наотносительно исходного.

Величину примите равной=( N + 5 G )/10 мс.

Найдите модуль и аргумент спектральной плотности смещенного импульса e₂(t) (рис.2.2б), представьте их в графическом виде, подобно рис.2.3, и сопоставьте полученные результаты. Зафиксируйте с необходимыми объяснениями, какие изменения произошли в спектрах за счет смещения импульса во времени.

Определите в интервале от 0 до 2значение спектра фазимпульсаe₂(t) на частоте= 100(50+(-1)^NN) рад/с.

Увеличьте длительность (ширину) импульса (рис.2.2а) в раз, приняв= ( 80 - N - 4 G )/10.

Рассчитайте и постройте кривую спектральной плотности амплитуд для импульса длительностью, где=1 мс. Опишите словами, какое изменение претерпел спектр исходного импульса (рис.2.2а) при увеличении его длительности.

Определите значение спектральной плотности амплитуд расширенного импульса на частоте .

9

Найдите, воспользовавшись теоремой сложения, комплексную спектральную плотность п а р ы импульсов (рис.2.4) с параметрами, указанными для первого и второго импульсов ( рис.2.2а и рис.2.2б соответственно).

Представьте функцию в графическом виде. Определите значение(микровольт умножить на секунду) на частоте= 100(50+(-1)^NN) рад/с.