
- •Кафедра автоматизированных и вычислительных систем
- •3.1. Методы минимизации логических функций на основе прямых преобразований сднф
- •3.2. Метод испытания импликант
- •3.3. Визуальные методы минимизации логических функций
- •3.3.2. Метод минимизации полностью определенных логических функций с помощью карт Карно
- •3.3.3. Метод минимизации частично определенных логических функций с помощью карт Карно
- •Содержание
- •Минимизация логических функций и их реализация на плм
- •394026 Воронеж, Московский просп., 14
ГОУВПО «Воронежский государственный технический
университет»
Кафедра автоматизированных и вычислительных систем
МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ И ИХ
РЕАЛИЗАЦИЯ НА ПЛМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по дисциплине «Теория автоматов» для студентов
специальности 230101
"Вычислительные машины, комплексы, системы и сети"
заочной формы обучения
Воронеж 2009
Составители: канд.техн. наук Ю.С. Акинина,
канд. техн. наук С.В. Тюрин
УДК 519.713(075)
Минимизация логических функций и их реализация на ПЛМ: методические указания по выполнению контрольной работы № 2 по дисциплине «Теория автоматов» для студентов специальности 230101 "Вычислительные машины, комплексы, системы и сети" заочной формы обучения / ГОУВПО «Воронежский государственный технический университет»; сост. Ю.С. Акинина, С.В. Тюрин. Воронеж, 2009. 29 с.
Методические указания содержат краткие теоретические сведения и задания для получения первичных навыков по практическому решению задач логического проектирования достаточно простых узлов цифровой вычислительной техники.
Предназначено для студентов второго курса.
Методические указания подготовлены на магнитном носителе в текстовом редакторе Microsoft Word 2002 и содержатся в файле ТА_ЗО_кр2.doc
Табл. 5. Ил. 9. Библиогр.: 6 назв.
Рецензент канд. техн. наук, доц. А.М. Нужный
Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. С.Л. Подвальный
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
ГОУВПО “Воронежский государственный технический университет”, 2009
1. ПОНЯТИЕ ЭЛЕМЕНТНОГО БАЗИСА И ИХ ОСНОВНЫЕ РАЗНОВИДНОСТИ
Любую логическую функцию в алгебре логики можно представить в виде СДНФ и СКНФ, используя три элементарные логические функции: инверсию, конъюнкцию и дизъюнкцию. Данный набор представляет собой полный функциональный набор.
Система функций алгебры логики f1, f2, …, fm называется функционально полной, если любая логическая функция от произвольного числа n – аргументов может быть представлена суперпозицией функций f1, f2, …, fm.
Система логических функций, обладающая функциональной полнотой, называется функциональным базисом, а набор элементов, реализующих эти функции, называется элементным базисом.
Минимальным базисом называется такой базис из f1, f2, …, fn, для которого удаление хотя бы одной из функций fi, входящих в этот базис, превращает систему функций f1, f2, …, fm в неполную [1].
Если осуществить преобразования над логическими функциями, заданными СДНФ и СКНФ по правилам де Моргана, взяв от них двойное отрицание, то получим функционально полные базисы, состоящие из одной или двух элементарных функций.
Функциональной полнотой обладают следующие элементные базисы:
1. И, ИЛИ, НЕ (основной базис);
2. И, НЕ;
3. ИЛИ, НЕ;
4. И-НЕ;
5. ИЛИ-НЕ;
6.
1, И,
![]() .
.
Для определения функционально полных систем логических функций необходимо для них определить наличие следующих пяти свойств [2]:
1.
Свойство
сохранения нуля:
данным свойством обладают те логические
функции, для которых справедливо
соотношение:![]() ,
т.е. на нулевом наборе аргументов,
логическая функция принимает нулевые
значения.
,
т.е. на нулевом наборе аргументов,
логическая функция принимает нулевые
значения.
2.
Свойство
сохранения единицы:
данным свойством обладают те логические
функции, для которых справедливо
соотношение:![]() ,
т.е. на единичном наборе аргументов,
логическая функция принимает единичные
значения.
,
т.е. на единичном наборе аргументов,
логическая функция принимает единичные
значения.
3.
Свойство
самодвойственности:
данным свойством обладают те логические
функции, для которых справедливо
соотношение:![]() ,
т.е. самодвойственной является функция,
у которой инвертирование значений всех
аргументов приводит к инвертированию
значений функции.
,
т.е. самодвойственной является функция,
у которой инвертирование значений всех
аргументов приводит к инвертированию
значений функции.
4. Свойство монотонности: функция обладает этим свойством, если для любой последовательности наборов, в каждом из которых аргументы не убывают, значения функции также не убывают, при этом полагаем, что 0<1.
5. Свойство линейности: данным свойством обладают те логические функции, которые могут быть представлены в следующем виде:
![]() ,
где
,
где
![]() .
.
Теорема Поста: Для того, чтобы множество N двоичных функций было базисом необходимо и достаточно, чтобы:
1. N содержало бы по крайней мере одну функцию, не сохраняющую ноль;
2. N содержало бы по крайней мере одну функцию, не сохраняющую единицу;
3. N содержало бы по крайней мере одну функцию, немонотонную;
4. N содержало бы по крайней мере одну функцию, несамодвойственную;
5. N содержало бы по крайней мере одну нелинейную функцию.
Контрольные вопросы:
1.1. Сформулируйте определение функционально полной системы функций алгебры логики.
1.2. Перечислите свойства элементарных логических функций, влияющих на формирование функционально полных логических базисов.
1.3. Сформулируйте теорему Поста.
2. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ В БАЗИСАХ И-НЕ, ИЛИ-НЕ ПО КНФ И ДНФ
Для того, чтобы реализовать логическую функцию, заданную в ДНФ в базисе И-НЕ необходимо взять двойное отрицание от этой функции и по законам де Моргана заменить все дизъюнкции на конъюнкции, т.е.:
![]() .
.
Для того, чтобы реализовать логическую функцию, заданную в ДНФ в базисе ИЛИ-НЕ необходимо взять четверное отрицание от этой функции и по законам де Моргана заменить все дизъюнкции на конъюнкции, т.е.:
![]() .
.
Для того, чтобы реализовать логическую функцию, заданную в КНФ в базисе ИЛИ-НЕ необходимо взять двойное отрицание от этой функции и по законам де Моргана заменить все конъюнкции на дизъюнкции, т.е.:
![]() .
.
Для того, чтобы реализовать логическую функцию, заданную в КНФ в базисе И-НЕ необходимо взять четверное отрицание от этой функции и по законам де Моргана заменить все конъюнкции на дизъюнкции [1,3], т.е.:
![]() .
.
Контрольные вопросы:
2.1. Перечислите известные Вам функциональные базисы.
2.2. Как реализовать в базисах И-НЕ, ИЛИ-НЕ инверсию одной переменной?
2.3. Можно ли по полученной логической схеме в базисе И-НЕ узнать, в каком виде первоначально была задана логическая функция (в ДНФ или в КНФ)?
3. МИНИМИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ.
Целью минимизации логических функций является получение более простых аналитических выражений, что в свою очередь позволит осуществить более простую минимизацию соответствующего комбинационного автомата.
Для рассмотрения вопроса минимизации необходимо сформулировать следующие определения.
Совершенной
дизъюнктивной нормальной формой (СДНФ)
логической
функции
![]() называется дизъюнкция элементарных
конъюнкций максимального ранга,
соответствующих наборам входных
переменных, на которых значение логической
функции равно 1.
называется дизъюнкция элементарных
конъюнкций максимального ранга,
соответствующих наборам входных
переменных, на которых значение логической
функции равно 1.
Дизъюнктивной
нормальной формой (ДНФ)
логической
функции
![]() называется дизъюнкция элементарных
конъюнкций функции, ранг хотя бы одной
из которых меньше максимального ранга.
называется дизъюнкция элементарных
конъюнкций функции, ранг хотя бы одной
из которых меньше максимального ранга.
Сокращенной
дизъюнктивной нормальной формой
логической функции
![]() называется такая ДНФ, реализующая
называется такая ДНФ, реализующая![]() ,
которая состоит из элементарных
конъюнкций, ранг хотя бы одной из которых
меньше максимального ранга и которые
не могут быть более склеены между собой.
Такие элементарные конъюнкции принято
называтьимпликантами.
,
которая состоит из элементарных
конъюнкций, ранг хотя бы одной из которых
меньше максимального ранга и которые
не могут быть более склеены между собой.
Такие элементарные конъюнкции принято
называтьимпликантами.
Тупиковой
дизъюнктивной нормальной формой
логической функции
![]() называется такая ДНФ, реализующая
называется такая ДНФ, реализующая![]() ,
в которой ни одна из импликант не является
лишней, то есть ни одна из импликант не
может быть удалена из формулы.
,
в которой ни одна из импликант не является
лишней, то есть ни одна из импликант не
может быть удалена из формулы.
Кратчайшей
дизъюнктивной нормальной формой
логической функции
![]() называется такая ДНФ, реализующая
называется такая ДНФ, реализующая![]() ,
в которой количество импликант минимально
по сравнению с другими ДНФ, реализующими
функцию
,
в которой количество импликант минимально
по сравнению с другими ДНФ, реализующими
функцию![]() .
.
Минимальной
дизъюнктивной нормальной формой
логической функции
![]() называется такая ДНФ, реализующая
называется такая ДНФ, реализующая![]() ,
в которой минимально количество букв
переменных по сравнению с другими ДНФ,
реализующими функцию
,
в которой минимально количество букв
переменных по сравнению с другими ДНФ,
реализующими функцию![]() .
.
Общую схему минимизации логических функций можно проиллюстрировать следующим образом:

Задача минимизации логических функций осложнена следующими обстоятельствами:
Общее количество ДНФ логической функции
 ,
зависящей отn-переменных,
определяется величиной
,
зависящей отn-переменных,
определяется величиной
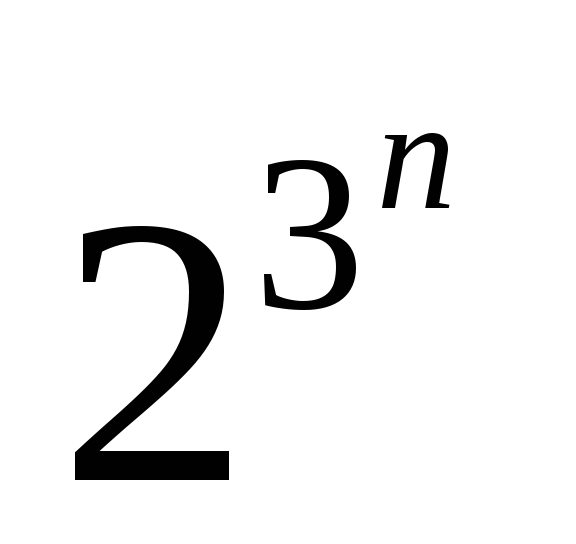 .
Число “3” определяется тем, что возможны
три исхода: любая логическая переменная
может входить в ДНФ со значением
инверсии, без знака инверсии, может не
входить в элементарную конъюнкцию, то
есть
.
Число “3” определяется тем, что возможны
три исхода: любая логическая переменная
может входить в ДНФ со значением
инверсии, без знака инверсии, может не
входить в элементарную конъюнкцию, то
есть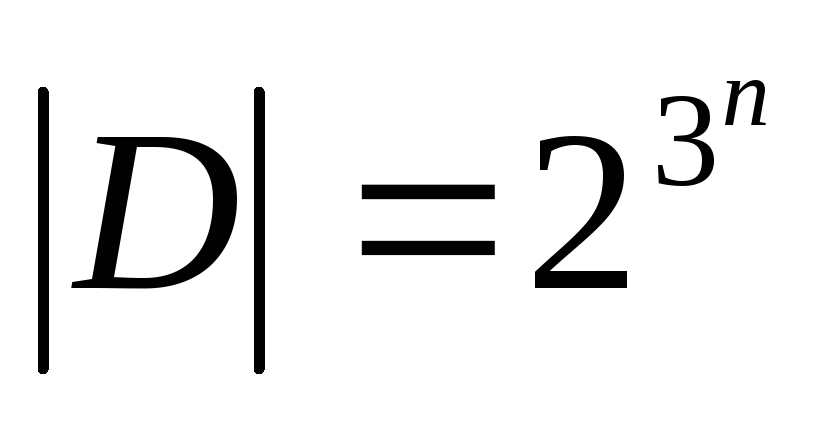 ,
где
,
где - мощность множестваD,
состоящего из объектов ДНФ логической
функции
- мощность множестваD,
состоящего из объектов ДНФ логической
функции
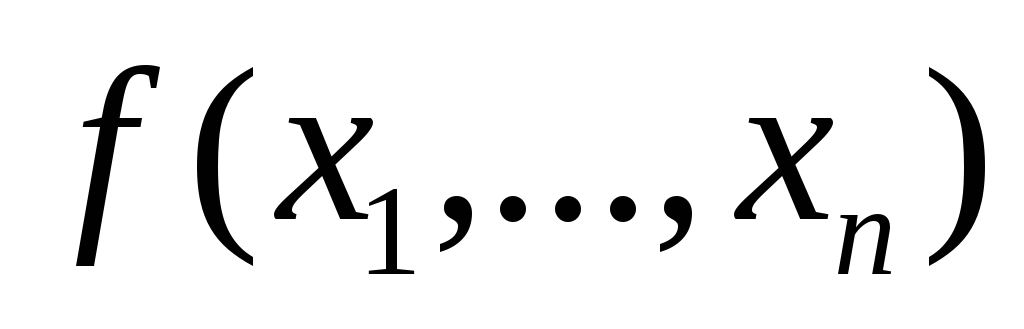 [1,4].
[1,4].Среди множества D содержится одна единственная СДНФ логической функции
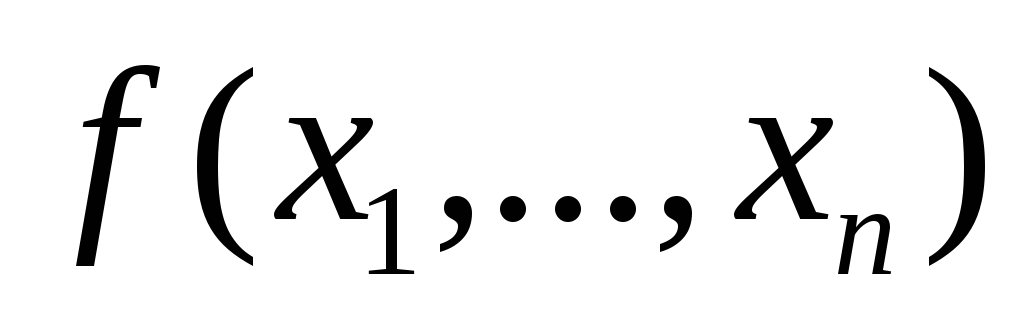 и некоторое количество тождественных
ей сокращенных и тупиковых ДНФ,
реализующих функцию
и некоторое количество тождественных
ей сокращенных и тупиковых ДНФ,
реализующих функцию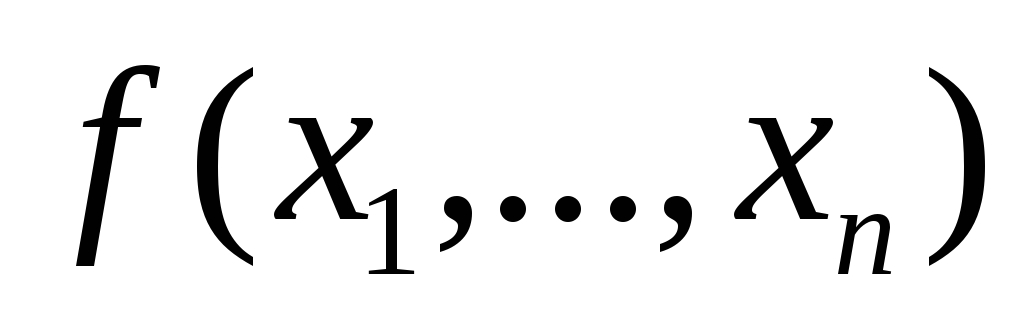 .
В настоящее время не существует
какого-либо способа определения общего
количества тождественных ДНФ, реализующих
одну и ту же логическую функцию.
.
В настоящее время не существует
какого-либо способа определения общего
количества тождественных ДНФ, реализующих
одну и ту же логическую функцию.Вид тождественной ДНФ логической функции существенно зависит от формы записи СДНФ и порядка преобразований, производимых над СДНФ логической функции.
Все известные на сегодня способы минимизации логических функций могут быть поделены на 2 большие группы:
Методы минимизации одновыходных (одиночных) логических функций.
Методы минимизации системы логических функций, зависящих от n-аргументов.
Среди методов первой группы выделяют следующие методы: прямые преобразования логических функций, визуальные методы минимизации с помощью специальных таблиц, машинно-ориентированные методы минимизации.
Все методы минимизации одновыходных логических функций базируются на следующих операциях:
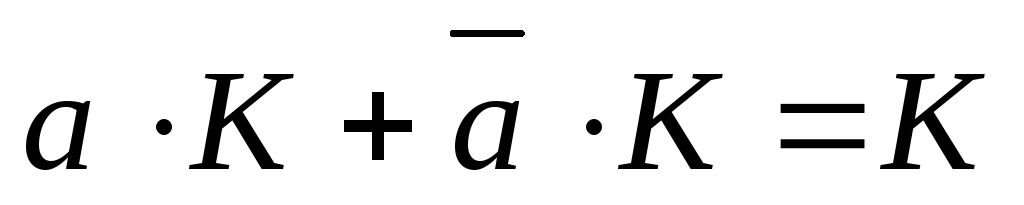 -
склеивание, где
-
склеивание, где
 - переменная, К – элементарная конъюнкция.
- переменная, К – элементарная конъюнкция.
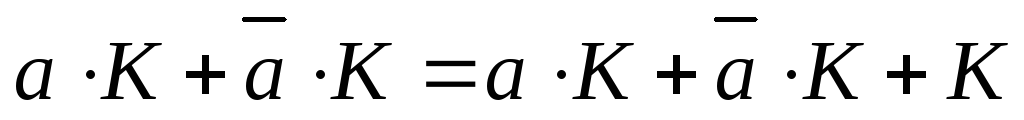 -
неполное склеивание.
-
неполное склеивание.
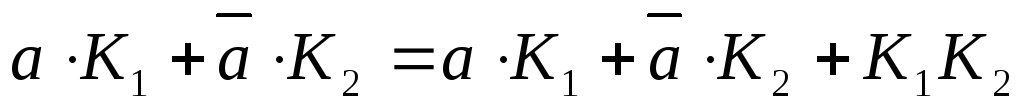 -
обобщенное склеивание.
-
обобщенное склеивание.
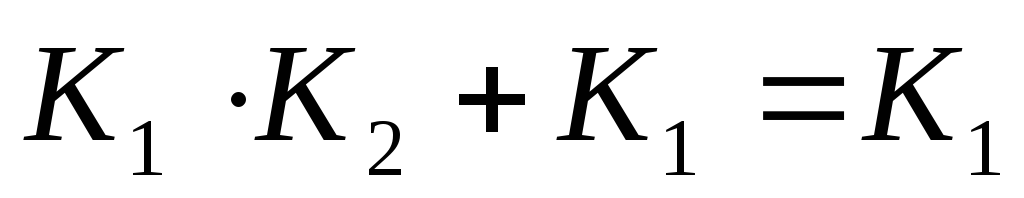 -
поглощение.
-
поглощение.
