2.1. Процедура обращения к порту.
Для того, чтобы обратится к порту, необходимо знать его адрес, назначение и, в соответствии с последним, направление передачи данных при работе.
В данной работе, при написании программ используется пакет Delphi. В состав стандартных средств программирования среды Delphi, возможность прямого обращения к портам ввода-вывода не входит. Ввиду этого для работы с портами используется специально написанный библиотечный модуль ports. Он содержит две процедуры, написанные на машинно-ориентированном языке программирования Ассемблер. Одна из этих процедур – outport(adress,data) – предназначен для вывода (записи) заданного значения в порт, с заданным адресом.При её вызове в порт с адресом adress записывается значение переменной data. Другая процедура – inport(adress,data) служит для ввода (считывания) данных из порта. В процессе выполнения эта процедура считывает данные в переменную data из порта с адресом adress. Тип переменной, используемой в качестве adress должен быть word? Тип data – byte.
unit ports;
Interface
procedure outport(adress :word;data :byte);
procedure inport(adress :word;var data :byte);
Implementation
procedure outport(adress :word;data :byte);
begin
asm
mov dx,adress
mov al,data
out dx,al
end
end;
procedure inport(adress :word;var data :byte);
Var regal : byte;
begin
asm
mov dx,adress
In al,dx
mov regal,al
end;
data:=regal;
end;
end.
Этот модуль подключается к основной программе через меню Delphi.
Для использования описанных процедур необходимо завести две переменные, например a и b, с типами word и byte соответственно. Значение
первой использовать в качестве адреса; второй – для хранения вводимых/выводимых данных. Для вывода данных в порт необходимо: присвоить его адрес переменной a; установить b, равной записываемому значению; вызвать процедуру outport(a,b). Для считывания данных из порта:
присвоить адрес порта переменной a; вызвать процедуру inport(a,b); в качестве данных использовать значение переменной b (процедура устанавливает её значение соответствующим образом). Переменные типа word
могут принимать значения 0..65535; типа byte – 0..255. Необходимо иметь
ввиду, что в используемых ИВК все порты однонаправлены, т.е. если записать, скажем, число value в порт с адресом adr , а затем считать из порта
adr, то мы не получим исходного value.
Для последующей математической обработки результатов измерений
необходимо полученные данные записать в текстовый файл. Ниже приведен фрагмент программы, обеспечивающий эту операцию.
{ переменные__________, задаваемые в разделе описания переменных соответствую
щей процедуры:
const
k=500; количество элементов выборки
var
f: text; текстовая файловая переменная}
.................................……………………
assign(f,'path_to_file\file_name'); {связать внешний файл file_name с
файловой переменной f }
rewrite(f); { создать и открыть файл}
for i:=1 to k do
writeln(f,x[i]); {запись массива данных x[i] столбцом в файл}
close(f); {закрыть файл}
………………………………………….
3.1. Основные уравнения.
Процессы,
протекающие в сплошной среде (жидкости,
газе) описываются уравнениями
гидродинамики. Для описания широкого
круга явлений достаточно трёх переменных,
характеризующих среду плотности ρ
средней скорости
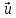и температуры T
(
или
давления р).
Координатные и временные зависимости
этих параметров описывающие данный
процесс т.е. функции ρ(
;
(
;T
(
;
можно найти решения из трёх основных
уравнений гидродинамики:
Уравнение непрерывности
Уравнение элемента движения жидкости массой dm=ρdV можно получить, полагая, что в общем случае на него действуют силы:
а) нормального давления на поверхности перпендикулярные этим силам.
б) без всякого трения на поверхности, движущиеся относительно соседних слоёв жидкости.
Под действием этих сил элемент жидкости движется с ускорением
Где
параметр v=
называется кинематической связью.
Это уравнение (Навье-Стокса) в частном случае пренебрежения вязкостью носит название уравнения Эйлера:
Уравнения () и () дополняются уравнением процесса, связывающим в стационарном процессе давление и плотность. В достаточно общем случае процесса, в котором не меняются внутренние свойства процесса молекул газа, т.е. идущего с постоянной теплоёмкостью С соответствующее уравнение (политропы) имеет вид:
Р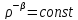
Где
параметр
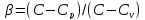носит
название показателя показателя политропы.
Уравнения
() или () образуют полную систему уравнений
гидродинамики на три переменные ρ(
;
(
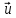;T
(
.
Выясним
теперь, при каких условиях можно
пренебречь вязкостью. Для этого сравним
в уравнении () вторые члены в левой и
правой частях. Обусловленные
пространственной неоднородностью
профиля скорости
.
Оценим эти члены:
,
,
Где U и L- соответственно характерная скорость и характерный пространственный масштаб изменения скорости т.е. неоднородности системы. Например, в случае обтекания шарика потоком жидкости в качестве характерной скорости U естественно взять невозмущённую скорость потока вдали от шарика, а в качестве характерного масштаба радиус шарика R.
Безразмерный параметр, равный отношению этих величин.
Носит название числа Рейнольдса и характеризует вклад вязкостного члена в уравнение. При больших числах значения числа Рейнольдса (Re>>1) эффектами связанными с вязкостью можно пренебречь, напротив, при Re<1 вязкость становится определяющим эффектом.
Движение тела в жидкости (газе) не редко сопровождается образованием волн, завихрений и т.д. различных временных и пространственных масштабов при которых движение жидкости приобретает турбулентный характер. Из общих соображений ясно, что вязкость гасит этот эффект, выравнивая все неоднородности и превращая энергию турбулентного движения жидкости в тепло. Следовательно, энергия может носить турбулентный характер только в случае больших значений Re. Напротив, в области малых значений Re значение жидкости носит упорядоченный ламинарный характер.
Получим также важный частный случай уравнения Эйлера для движения с постоянной скоростью. С помощью формулы:
Преобразуем уравнение при u=const (по времени) к виду
Введём теперь понятие линии тока, в каждой точке которой скорость жидкости направлена по касательной к ней, иными словами жидкость движется вдоль тока. Уравнение линии тока имеет вид:
Для
широкого класса течений, в которых линии
тока не образуют замкнутых фигур т.е.
течение не образует вихрей
уравнение приобретает вид:
Такое течение называется без вихревым или потенциальным.
Предположим для простоты, что жидкость несжимаема (можно получить тот же результат и в общем случае) находим:
В плоском случае эта формула приобретает вид
или
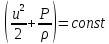
Где константа зависит от линии тока, а производная берётся вдоль этой линии. Формула () носит название уравнения Бернулли и определяет интеграл стационарного уравнения для потенциального течения.