4

Лекция 9 Регрессионные модели

1. Регрессионные модели в экологии

Понятие регрессии. Корреляционную зависимость между двумя переменными величинами можно описать разными способами. В частности, любая форма связи может быть выражена уравнением общего вида

у = f(x)

Где у – зависимая переменная величина или функция от независимой переменной х, называемой аргументом.

Регрессией называется изменение функции в зависимости от изменений одного или нескольких аргументов.

Для выражения регрессии служат эмпирические и теоретические ряды, их графики – линии регрессии, а также уравнения регрессии и коэффициенты регрессии.

Ряды регрессии, особенно их графики дают наглядное представление о степени корреляционной связи между исследуемыми переменными. Форма связи между переменными может быть разнообразной. Задача состоит в том, чтобы эту форму выразить уравнением определенной функции, что позволяет получить нужную информацию о соответствии между переменными величинами и предвидеть возможные изменения одной переменной (функции) в зависимости от изменения другой переменной (аргумента).

Регрессионные модели широко применяются при исследовании зависимости плодородия почв и урожайности сельскохозяйственных культур от агроклиматических и агротехнических факторов.

Используются следующие виды функций.

Линейная функция:

у = а₀ + ах

Л

а₀

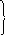инейную функцию используют при первоначальном изучении факторов, влияющих на урожайность, а также для отсеивания незначительных или малозначащих факторов. Однако она сильно искажает реальные зависимости, которые, как правило, являются нелинейными. При наличии нескольких факторов линейная функция выглядит так:

у = а0 +	n	aiхi
	∑
	i=1

Лучшее приближение к реальности при интерполяции дает квадратичная (параболическая) функция:

у = а₀ + а₁х + а₂х²

Эту зависимость уже можно продифференцировать и исследовать на максимумы и минимумы. Максимум достигается в той точке, где х = а₁/2а₂.

Квадратичная функция для более чем одной переменной имеет форму:

у = а₀ + ∑a_ix_i + ∑a_iix_i² + ∑a_ijx_ix_j

3. Степенная функция:

y = ax^b

при многофакторной зависимости имеет вид

y = ax₁^b1*x₂^b2*x₃^b3…x_n^bn

Для степенной функции характерен ряд положительных свойств: компактность, небольшое число расчетных параметров, возможность определения вторых производных и исследования функции на экстремум. Путем логарифмирования степенную функцию можно свести к линейной:

logy = loga + b₁logx₁ + b₂logx₂ + b₃logx₂ + … + b_nlogx_n

это облегчает определение параметров функции и решение задач оптимизации факторов.

4. Показательная функция Спиллмана

у = М-АР^х

где М – максимум функции, А – постоянная величина, показывающая разность между М и у при х = 0; Р – постоянная < 1 величина.

Если функция Спиллмана рассматривается в зависимости от нескольких факторов, она выражается следующим образом:

y = М(1 – Р₁^х1)(1 - Р₂^х2) … (1 – Р_n^xn)

Экспоненциальная функция:

у = ае^bx

5. Модифицированная экспоненциальная функция

у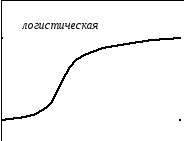 = k - ae^bx

Логистическая функция (S-образная)

у = k/(1 + be^-cx)

6. Квадратичная логистическая функция

у = k/(1 + be^-cx)²

7. Гиперболическая функция

у = а + 1/(с + х)

8. Гиперболическая Лйнуивера-Берка функция

у = Мх/(А + х)

Выбор соответствующего вида функции определяется от полученных в эксперименте данных и зависит от типа исследуемого явления.

Разработка регрессионных моделей – сложный процесс. Практическое использование таких моделей становится возможным при выполнении ряда требований.

Модель должна

учитывать все основные факторы, влияющие на изучаемое явление;

охватывать широкий диапазон изменчивости факторов;

обеспечивать достаточно точное измерение значений факторов, между которыми не должно быть внутренней связи (некоррелированность факторов);

должны быть известны значения факторов, не учитываемых моделью;

аппроксимирующая функция в наибольшей степени должна соответствовать реальным биогеохимическим закономерностям.

Следует отметить, что ни одна из перечисленных выше функций не обладает универсальностью в описании процессов, происходящих в системе «почва-климат-растительный покров-технология- урожай).

В зависимости от изучаемых процессов применима та или иная функция.

Специальные многофакторные исследования, проводимые по факториальным схемам, дают возможность установить более близкие к реальным количественные связи изучаемого явления с управляемыми факторами. Однако факториальные схемы не включают многие важные факторы, регрессионные модели имеют локальное применение, т.е. они правомерны в конкретных условиях проведения эксперимента. Поэтому ни одна из регрессионных моделей не может удовлетворить все основные требования. Часто бывает необходим целый комплекс моделей, для решения той или иной научной или практической задачи.

В агротехнологии интенсивно разрабатывались и разрабатываются регрессионные модели, выражающие зависимость урожая от основных факторов: показателей плодородия почвы, доз удобрений, орошения, приемов обработки почвы, климатических факторов и характера распределения осадков по периодам вегетации.

Например, для расчета прибавки урожая яровой пшеницы от доз NPK в зависимости от агротехнических свойств почвы и количества осадков на выщелоченных черноземах Европейской части России получена формула

∆У = (3,963 + 0,061Р₂О₅ – 0,62К₂О + 0,04ОС – 0,0002(Р₂О₅)² + 0,015рН*К₂О + 0,222N^0,5 + 0,001N^0,5ОС + 0,574Р^0,5 – 0,002Р^0,5Р₂О₅ + 0,075К^0,5рН – 0,0025К^0,5К₂О – 0,162(N+Р+К))*0,1

где ∆У – прибавка урожая от удобрений, т/га; N, Р, К – дозы действующего вещества азотных, фосфорных и калийных удобрений, кг/га; Р₂О₅ – содержание в почве подвижного фосфора, мг/100 г; К₂О – содержание в почве подвижного калия, мг/100 г; рН – кислотность почвы; ОС – сумма осадков за 60 дней со дня посева.