Неидеальный вклад в энтропию смешения

Если имеет место корреляция во взаимном размещении атомов, то есть вероятность нахождения атома данного компонента зависит от того, атомы каких компонентов располагаются в окрестных местах, то количество возможных конфигураций уменьшается. Некоторые из конфигураций становятся, как бы запрещенными и должны быть исключены из . К “запрету” определенных конфигураций приводит неравноценность мест, в частности ближний и дальний порядок. Введем формальноY– число “запрещенных” конфигураций. Тогда, вместобудем иметьи далее, где- вклад в конфигурационную энтропию обусловленный ближним и дальним порядком или корреляцией.

При этом всегда , в то время как

Поэтому всякое отклонение от идеального беспорядка дает в конфигурационную энтропию раствора аддитивный отрицательный вклад, Полная энтропия системы представится как (20).

Соответственно и энтропию смешения можно представить в виде суммы аналогичных вкладов. Из (17) видно, что отTне зависит, но существенно зависит от температуры. Меняется колебательный спектр и меняется колебательный беспорядок. Таким образом, неидеальный вклад в энтропию смешения раствора представлен суммой(21) является температурно-зависимым вкладом.

Тогда энтропию смешения можно записать в виде (22)

Растворы с идеальной энтропией смешения

Опыт и модельные соображения показывают, что при неограниченном повышении температуры иприближаются к нулю. Для ряда растворов при достаточно высоких температурах,экспериментально неотличимы от нуля или же отличаются незначительно. Это приводит к представлению о растворах с идеальной энтропией смешения

Для таких растворов (23)

(24)

Растворы с идеальной энтропией обладают следующими свойствами.

1. Поскольку не зависит отT, то

2. Из выражения, что у раствора с идеальной энтропией, т.е. энтальпия смешения не зависит от температуры.

3. Поскольку не зависит от давления, то, и следовательно, объемный не зависит от температуры.

4. Соотношение типа правила Неймана-Коппа выполняются так же для изохорной теплоемкости . Из этого следует. Следовательно энергия смешения при изохорном смешении не зависит от температуры.

Докажем, что если энтропия смешения одного из компонентов идеальна, то и энтропия смешения любого другого компонента идеальна, то есть и, следовательно, полная энтропия смешения идеальна

Для доказательства используем равенство между производными первого типа вдоль лучей, выходящих из вершин. (23)

Тогда , но из(23) (24)

Интегрируя (24) при фиксированных, получим, где- постоянная интегрирования, которую определяем при.. Отсюдаи окончательно

Идеальные растворы

Многие реальные растворы при достаточно высокой температуре приближаются к такому поведению, которое характеризуется одновременным выполнением условий ,, (25) или,

Растворы, для которых эти условия выполняются, называются идеальными. Для идеальных растворов

;

Если раствор идеален в отношении одного из компонентов, то он идеален и в отношении любого другого компонента и идеален в целом.

Идеальные растворы обладают теми же свойствами, что и атермические растворы ,,.

Предельные значения мольных парциальных функций.

Из следует.

Из (23) следует

Такими свойствами обладают, однако, не все мольные парциальные функции. Такие функции ,,присохраняют конечные значения. К такому выводу приводят простые соображения. Их удобно излагать в терминах атомных парциальных функций,и т.д.

Например, изменение внутренней энергии раствора u. При добавлении к нему атомаi-го компонента изменение внутренней энергии равно. Эта величина очевидно мала по сравнению сu.Поэтомуне может принимать бесконечно большое знасение при предельном разбавлении растворов.

То же можно сказать и об изменении объема.

При добавлении первых атомов i-го компонента в раствор вероятность их взаимодействия друг с другом пренебрежимо мала. Поэтому при достаточно малыхвеличины,,должны быть линейными функциями концентрации. Линейная экстраполяция этих функций кдает поэтому конечные значения,,. Однако по иному ведет себя идеальная энтропия смешения. Рассмотрим наиболее простой случай образования двухкомпонентного раствора.

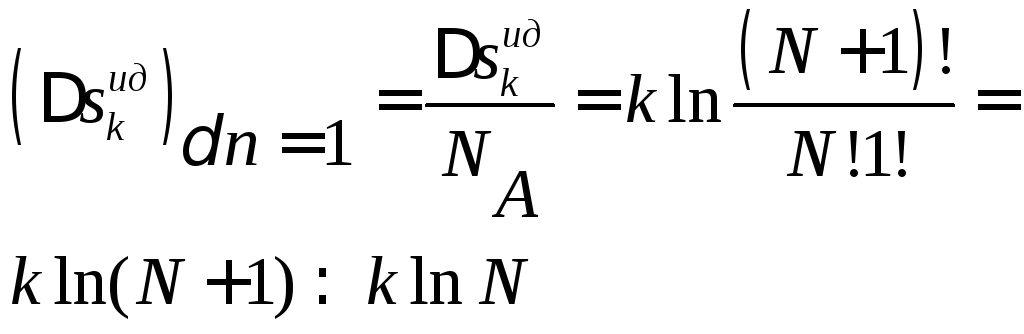
Хотя и мал по сравнению сN, но прии. Поэтому для макроскопических системоказывается большой величиной. При добавлении двух атомов компонентаi к чистому веществу

Добавление каждого последующего атома вызывает существенно меньшие изменения