
Модель регулярных твердых растворов
Раствор – любая макроскопически
однородная фаза переменного состава.
Растворам противопоставляются только
фазы постоянного состава или чистые
компоненты, а остальное все растворы.
Любая экстенсивная характеристика
раствора является функцией любых двух
простых параметров T,P,V,Sи набора величин {ni}.
Обычно в качестве независимых переменных
используютсяT,P
и{ni}.
Таким образом![]() (1)
(1)
В равновесии со средой T,P определяются средой и тогда уравнение (1)читается следующим образом.В равновесии со средой любая экстенсивная характеристика раствора является функцией внешних условий и состава раствора, а так же общего количества вещества. Индивидуальность раствора отражается в характере выражения (1) и входящих в выражение констант.
Поведение отдельного произвольного
компонента раствора может быть описано
производной
 , (2)
, (2)
Называемой мольной парциальной функцией
i-го компонента.
Это изобарно-изотермическая мольная
парциальная функция. Можно ввести
мольные другие мольные парциальные
функции. - это изохорно-изотермическая функция.
- это изохорно-изотермическая функция.
Существует формула аддитивности
![]() (3)
(3)
Запишем также обобщенное уравнение Гиббса – Дюгема.
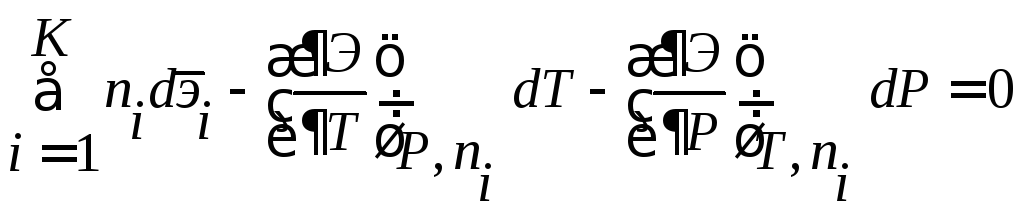 . (4)
. (4)
В конкретных случаях уравнения
Гиббса-Дюгема могут быть записаны
заменой Эна соответствующую
экстенсивную функцию![]() .
При заменеЭ→
.
При заменеЭ→![]() получим
получим![]() ,
(5)
,
(5)
Э→S получим ![]() ,
(6)
,
(6)
Э→Vполучим (7)
(7)
Э→Uполучим
![]() (8)
(8)
Функции смешения
Термодинамические функции определены в классической термодинамике с точностью до некоторой произвольной аддитивной величины. Абсолютное значение имеют лишь изменения функций по отношению к выбранному уровню отчета (стандартному состоянию).
В качестве стандартного состояния выбирается система (при тех же T,P, что и рассматриваемый раствор), в которой каждый из компонентов раствора присутствует в виде обособленной однокомпонентной фазы, при том же количестве вещества компонента, которое содержится в растворе. Чистые вещества следует при этом выбирать в том же фазовом состоянии (в том же агрегатном состоянии, с решеткой того же типа и с теми же параметрами решетки), что и в растворе.
Такой способ в ряде случаев вызывает затруднения в выборе стандартного состояния. Поскольку при перемешивании чистых компонентов могут образовываться химические соединения, возникают фазовые переходы в структуры, которые не наблюдаются у чистых компонентов.
Экстенсивная функция стандартного
состояния записывается в виде
 (9)
(9)
![]() - мольная функция чистого состоянияi-гокомпонента.
Отсчитанное от этого уровня экстенсивная
функцияЭсм.
равна
- мольная функция чистого состоянияi-гокомпонента.
Отсчитанное от этого уровня экстенсивная
функцияЭсм.
равна (10)
(10)
- представляет собой изменение Эпри образовании раствора. ЕЕ называют функцией смешения или растворения.. Аналогично вводятся т мольные парциальные функции смешения.
 (11)
(11)
 , (12)
, (12)
где
![]() и есть мольная парциальная функция
смешения, т.е. соответствующая мольная
парциальная функция смешения, отсчитываемая
от того значения, которое она принимает
при
и есть мольная парциальная функция
смешения, т.е. соответствующая мольная
парциальная функция смешения, отсчитываемая
от того значения, которое она принимает
при![]() .
Соответственно вводятся энтальпия
смешения
.
Соответственно вводятся энтальпия
смешения![]() ,
энергия Гиббса
,
энергия Гиббса![]() ,
объем
смешения
,
объем
смешения![]() ,
,
энтропия смешения
![]() ,
,
Изобарная теплоемкость смешения
![]() и т.д.
и т.д.
Теплота смешения
Во всех случаях будем понимать изобарно изотермическую теплоту смешения. Опыт показывает, что теплота смешения, при изобарно-изотермическом образовании раствора может расти, а может убывать h>0, h<0.
При изобарно-изотермическом смешении тепловой эффект смешения равна энергии смешения.
Растворы с h>0называется эндотермическим (тепло поглощается системой).
Растворы с отрицательной теплотой смешения – экзотермические (система выделяет тепло).
Для многих растворов более или менее
выполняется
![]() Такие растворы называются атермическими.
Такие растворы называются атермическими.
