2013.Термодинамика / 23Лекция_II_9-28-09-2012

При образовании бинарного раствора энергия смешения Гиббса , или выражая через парциальные величины

Аналогично можно записать для теплот смешения

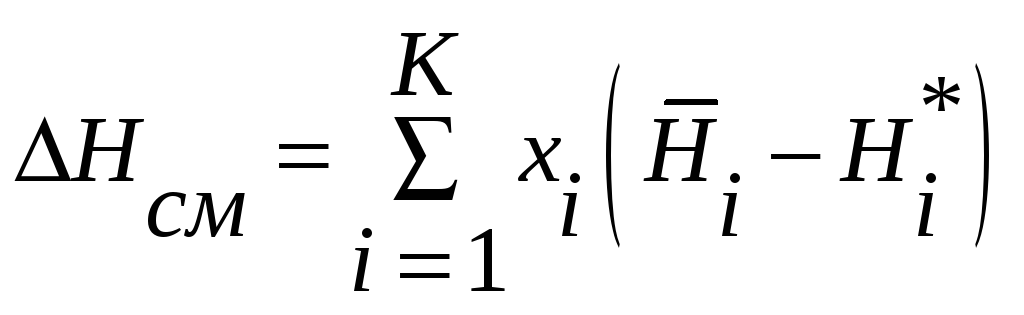
Для энтропии 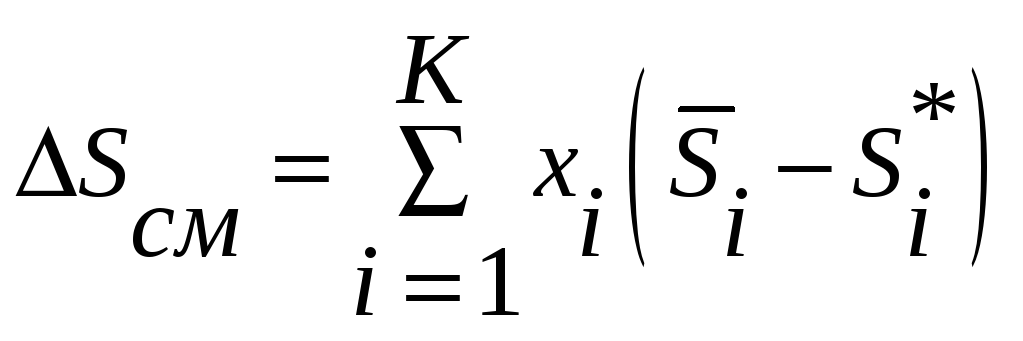. Для идеального раствора активность равна концентрации

Равновесие между фазами различного состава. Химический потенциал

Рассмотрим очень большое количество двух фаз, причем обе содержат компонент A. Компонент A в - фазе будет иметь активность , а в - фазе . Перенесем 1 г-атом компонента A из - фазы в - фазу при постоянной температуре. Пусть исходное количество элементов A и B столь велико по сравнению с одним г-атомом A, что состав изменится на бесконечно малую величину. Реакция, связанная с переносом вещества, запишется так ,

Компонент A в - фазе будет иметь свободную парциальную энергию Гиббса равную , а в- фазе она будет выражаться и свободная энергия реакции переноса запишется .

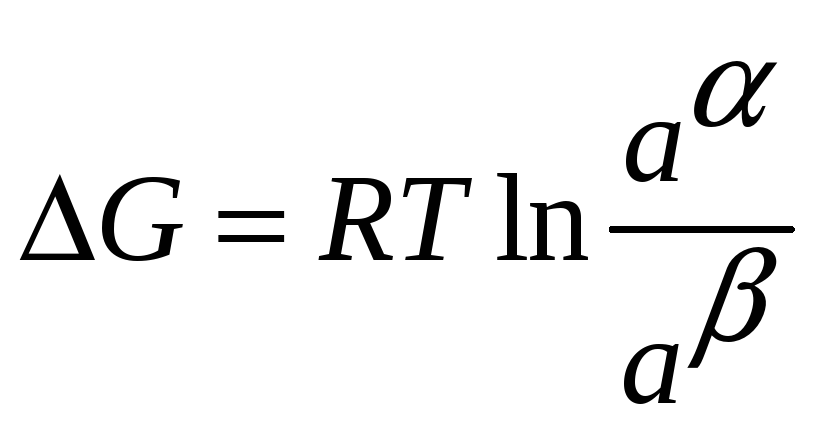Величину - (для одного моля) называют химическим потенциалом и обозначают . Если , то реакция будет происходить самопроизвольно, Поскольку в этом случае .

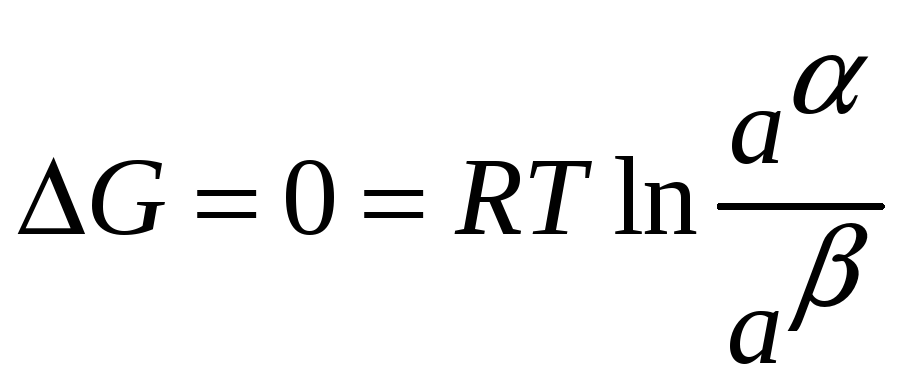
Если состав изменится до такой степени, что достигается равновесие то . Как правило, содержание компонента A в фазах не бывает равным, поскольку неодинаковы коэффициенты активности A в разных фазах.

Это способ используется для определения коэффициента активности в одной фазе, если известен коэффициент активности в другой. Обычно он применяется к жидкостям. В твердой фазе очень трудно достигнуть равновесия.

Активности компонентов A в обеих фазах должны относиться к одному и тому же стандартному состоянию, иначе выражение не будут сокращаться.

Использование диаграмм состояния получение термодинамических данных

Рассмотрим случай, когда компонент растворим в пределах в при данной температуре T, а A имеет бесконечно малую растворимость в B. Такое положение можно проиллюстрировать на диаграмме состояния. Таким образом, в состоянии равновесия при для любого состава , , чистый компонент B будет находится в равновесии с B в -фазе при составе , т.е. для реакции

(1)

Следовательно, ,.

Поскольку чистый элемент B находится в стандартном состоянии, то (по определению) . Если раствор разбавлен, можно предположить, что компонент B в нем следует закону Генри, и в результате можно рассчитать коэффициент активности . Следовательно

Можно получить сведения о форме линии ограниченной растворимости - фазы, как функции температуры для диаграммы состояния этого типа.

У равнение (1) равновесной реакции растворения для этой цели не подойдет поскольку . Нужно рассмотреть другое уравнение растворения. Пусть компонент B переносится из чистого состояния в какой-либо произвольный состав в , например в , вместо . Таким образом,

Рассчитаем теперь . Исходя из основных положений термодинамики.

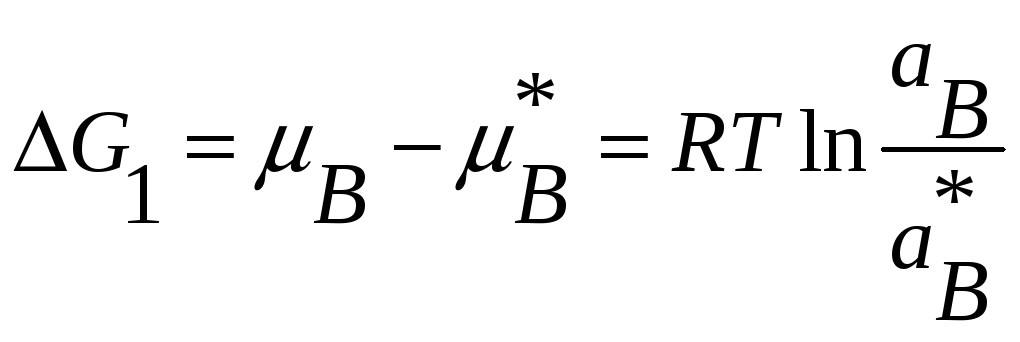, где , как и прежде, а .

Таким образом,

Кроме того, известно термодинамическое соотношение 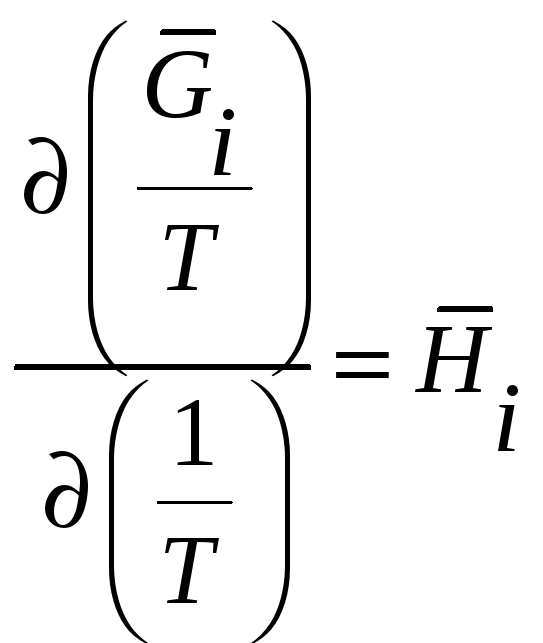. Поэтому

,

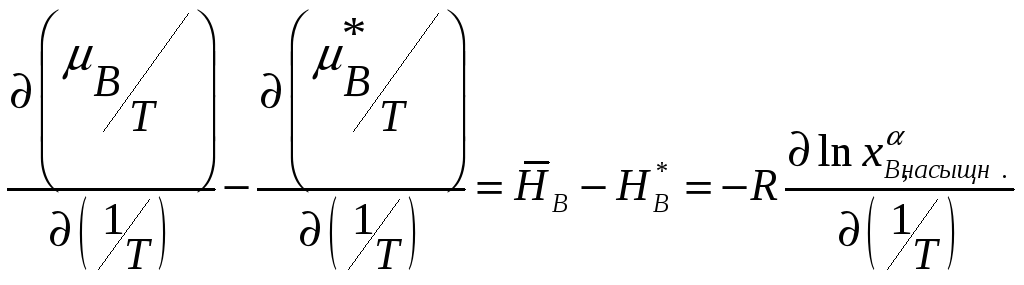
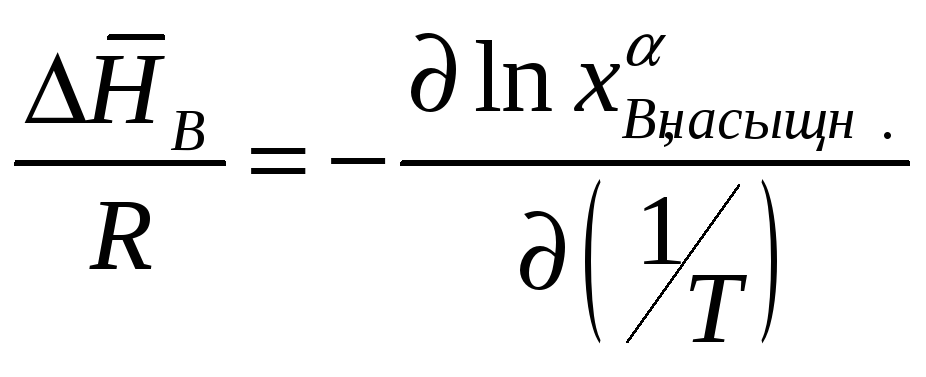Из рассматриваемой нами реакции следует, что соответствует энтальпии, расходуемой на перенос чистого компонента B в разбавленный раствор. Эта величина является относительной парциальной энтальпией.

В разбавленном твердом растворе, в котором растворенное вещество следует закону Генри, не зависит от состава. В этом случае можно получить из линии ограниченной растворимости. , как и большинство реакций в твердом теле не зависит от температуры. Если нанести экспериментальные данные на график в зависимости от , получим линию весьма близкую к прямой, с наклоном

В еличина для твердых растворов, так что увеличивается с ростом температуры.

Если рассмотреть с точки зрения статистической механики, то мы получим изменение энтропии.

Парциальная энтропия смешения на атом . Кроме конфигурационной энтропии изменяется еще и колебательная энтропия. Тогда изменение парциальной энтропии на атом будет равно . Кроме того, при переносе атома из чистого компонента B в раствор происходит изменение энтальпии . С учетом всего изменение химического потенциала на атом выразится

. При равновесии , для состава , и мольные доля B в равна Таким образом константа A равна . Логарифмируя (1)

Если нанести на график в зависимости от обратной температуры 1/T и про экстраполировать к 1/T=0, второе слагаемое становится равным нулю, а отрезок от начала координат до точки пересечения равен .

Таким образом, получается метод оценки колебательной энтропии растворенного вещества по отношению к значению энтропии чистого вещества.

Для большинства систем верхний уровень применимости уравнения (1) составляет 1%. Уравнение (1) можно видоизменить, сделав разложение экспонент в ряд Тейлора с сохранением слагаемых до второго порядка. Тогда получим

Для систем рассматриваемого типа. Пределы применимости этого уравнения значительно больше.

Пусть элементы A и B ограниченно растворимы друг в друге. Диаграмма состояния, отвечающая этому случаю имеет вид.