
Костюк - Основы программирования
.pdf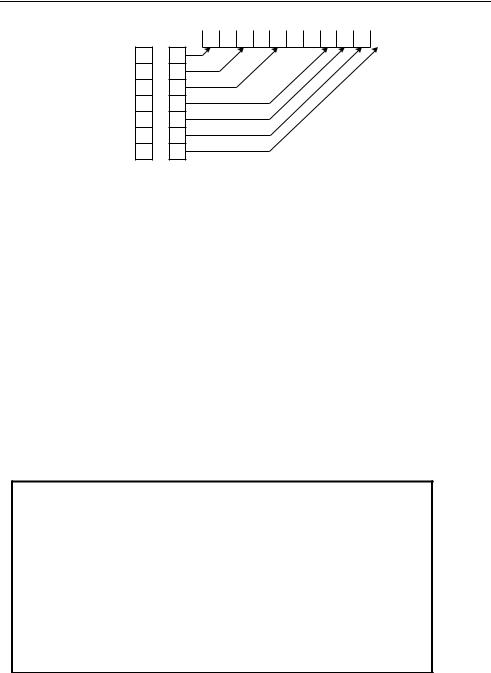
111
L |
S D |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2 3 1 3 1 2 4 3 6 5 |
|
|
||||||||||
2 |
1 |
2 |
3 |
3 |
5 |
1 |
8 |
1 |
9 |
1 |
10 |
0 |
11 |
Рис. 6.2
Чтобы определить, имеется ли ребро (дуга), соединяющее вершины i и j, необходимо среди элементов i–го списка: D[S[i]], ..., D[S[i]+L[i]-1] найти
элемент, равный j. При упорядоченности списков можно использовать алгоритм
дихотомического поиска.
Чтобы просмотреть все вершины, смежные по ребрам с вершиной i (или вер шины, в которые идут дуги из i), необходимо перебрать все элементы i–го списка. А для просмотра вершин, из которых идут дуги в вершину i, необходимо перебрать все списки, т.е. все элементы массива D.
При удалении ребра между вершинами i и j можно уплотнить не весь массив D, а только i–й и j–й списки, уменьшив на 1 элементы L[i] и L[j], на что
потребуется не более 2∙n шагов. В то же время при вставке ребра потребуется в худшем случае переписывать весь массив D.
Рассмотрим формирование массивов D, S и L для задания графа.
Пример 6.2. Пусть совокупность m ребер неориентированного графа из n вер шин задана c помощью массивов v1 и v2 так же, как в примере 6.1. Пусть также размеры массивов v1 и v2 достаточны для размещения 2*m элементов.
for i:=1 to m do {дублирование ребер в массивах v1 и v2} begin v1[i+m]:=v2[i]; v2[i+m]:=v1[i] end;
for j:=1 to n do |
L[j]:=0; |
{обнуление длин списков} |
|
for i:=1 to 2*m do |
L[k]:=L[i]+1 |
{вычисление длин списков} |
|
begin k:=v1[i]; |
end; |
|
|
S[1]:=1; {вычисление указателей на начала списков в массиве D} |
(6.2) |
||
for j:=2 to n do |
S[j]:=S[j-1]+L[j-1]; |
|
|
for j:=1 to n do |
U[j]:=S[j]; {дублирование указателей} |
|
|
for i:=1 to 2*m do |
{распределение смежных вершин} |
|
|
begin k:=v1[i]; |
|
{по спискам массива D} |
|
D[U[k]]:=v2[i]; U[k]:=U[k]+1 |
|
||
end; |
|
|
|
В алгоритме (6.2) вначале дублируются ребра так, чтобы наряду с парой вершин (k – l), задающих ребро, присутствовала пара (l – k). Затем подсчитываются длины

112
списков, которые будут позже размещены в массиве D. После этого подсчитываются указатели на начала этих списков. На завершающем этапе заполняется массив D,
при этом элементы распределяются по спискам за один просмотр благодаря вспомо гательным указателям массива U, отслеживающим свободные места по спискам. Не
трудно видеть, что трудоемкость всех этапов – линейная от числа вершин или ребер графа.
Если списки массива D требуется упорядочить, то необходим дополнительный этап, на котором каждый из списков сортируется независимо от других.
Конец примера.
Заметим, что если граф ориентированный, то первый этап (дублирование ребер)
в алгоритме (6.1) не нужен, а циклы на последующих этапах должны выполняться до m, а не до 2*m.
6.2 Просмотр неориентированного графа
Задача просмотра всех вершин графа с учетом ребер, связывающих их с соседни ми вершинами, является важным этапом при решении многих более сложных задач. Имеется два основных метода: просмотр графа вглубь и просмотр графа вширь. Про смотр может начинаться с любой начальной вершины. При этом вершины могут по лучить новые номера в порядке просмотра.
При просмотре вглубь в цикле ищется непросмотренная вершина, смежная с те кущей. Как только такая вершина обнаружится, алгоритм рекурсивно запускается с этой новой начальной вершины.
Пример 6.3. Рекурсивный алгоритм просмотра вглубь. Граф из n вершин задан матрицей смежности M. Массив R содержит номера вершин в порядке просмотра, причем R[i]=0, если вершина i не просмотрена.
procedure deеp(k:integer); var i: integer;
begin
for i:=1 to n do
if (M[k,i]=1)and(R[i]=0) then begin (6.3) nom:=nom+1; R[i]:=nom; deеp(i)
end;end
Перед вызовом процедуры всем n элементам массива R необходимо при своить нули, а переменной nom задать начальную нумерацию для той вершины k,

113
с которой начинается просмотр, и, кроме того, присвоить R[k]:=nom. После этого процедура deеp вызывается оператором deеp(k).
Завершимость алгоритма следует из того, что перед рекурсивным вызовом deеp(i) проверяется R[i]=0 и присваивается R[i]:=nom. Поэтому общее ко
личество вызовов не превышает n. Глубина рекурсии ограничена той же величиной n.
Если граф связный, то по математической индукции можно доказать, что будут просмотрены все его вершины. Если же граф несвязный, то будут просмотрены все те вершины, до которых можно добраться по ребрам из начальной вершины k, т.е. до всех вершин компоненты связности, куда входит вершина k.
Трудоемкость алгоритма определяется тем, что при каждом вызове процедуры цикл выполняется n раз, т.е. общая трудоемкость имеет порядок n2. Если граф за
дать списками или массивом смежных вершин, то не будет лишних выполнений цик ла для проверки несуществующих ребер, и тогда количество выполнений цикла бу дет равно удвоенному числу ребер.
Конец примера.
Используя алгоритм просмотра графа, можно решить задачу выделения компо нент связности графа.
Пример 6.4. Алгоритм выделения компонент связности графа из n вершин. Ал горитм формирует элементы массива C, определяющие компоненты связности для вершин графа. C[i]=q, если i–я вершина принадлежит q–й компоненте связно сти. Первоначально всем элементам массива C присваиваются нули, это означает,
что ни одна из вершин графа не отнесена ни к одной из компонент. Внешний цикл в алгоритме отыскивает очередную вершину, для которой C[i]=0, приписывает этой
вершине номер новой компоненты, после чего производит просмотр графа, начиная с этой вершины, присваивая всем вершинам компоненты (в массиве C) один и тот же
номер.
for i:=1 to n do C[i]:=0; q:=0;
for i:=1 to n do
if C[i]=0 then begin (6.4) q:=q+1; C[i]:=q;
cdeеp(i)
end;
Для использования в алгоритме (6.4) процедура deеp должна быть изменена та ким образом, чтобы в ней перед рекурсивным вызовом было присваивание C[i]:=q.
Алгоритм модифицированной процедуры cdeеp (6.5) приведен ниже. В ней, кроме того, используется другое представление графа – в виде массива смежных вершин, как в примере 6.2.

114
Нетрудно видеть, что общая трудоемкость алгоритма (6.4), включая время вы полнения процедуры cdeеp (6.5), имеет порядок n + m, где n – число вершин,
m – число ребер графа.
|
|
|
procedure cdeеp(k:integer); |
|
|
var |
i: integer; |
|
begin |
i:=S[k] to S[k]+L[k]-1 do |
|
for |
(6.5) |
|
begin j:=D[i]; |
||
|
if C[j]=0 then begin C[j]:=q; cdeеp(j) end |
|
end;end |
|
|
Конец примера.
При просмотре вширь заданной начальной вершине приписывается уровень 1. Затем в цикле ищутся все непросмотренные вершины, смежные с текущей, и им при писывается уровень, на единицу больший, чем уровень текущей вершины. Далее те кущей становится очередная вершина среди последовательности просмотренных вер шин и т.д. В результате всем вершинам, достижимым из начальной, приписывается уровень, на 1 больший, чем кратчайшее расстояние (измеряемое числом пройденных ребер) от начальной вершины.
|
Пример 6.5. Алгоритм просмотра вширь. Граф, содержащий |
n вершин, задан в |
|
виде массива смежных вершин. |
|
|
|
|
|
|
|
|
P[1]:=nom; r:=1; t:=1; |
|
|
|
for i:=1 to n do V[i]:=0; |
|
|
|
V[nom]:=1; |
|
|
|
while t<=r do |
|
|
|
begin k:=P[t]; q:=V[k]+1; |
|
|
|
for i:=S[k] to S[k]+L[k]-1 do |
|
|
|
begin j:=D[i]; |
|
(6.6) |
|
if V[j]=0 then begin |
|
|
|
V[j]:=q; r:=r+1; P[r]:=j |
|
|
|
end |
|
|
|
end; |
|
|
|
t:=t+1 |
|
|
|
end; |
|
|
В массиве V записываются уровни для просмотренных вершин, в массиве P – номера просмотренных вершин. Размер этих массивов – n. Первоначально элемен ту P[1] присваивается номер начальной вершины nom, элементу V[nom] – еди ница, а всем остальным элементам массива V – нули. Переменная r обозначает ко

115
личество просмотренных вершин, а переменная t – элемент в массиве V, содер
жащий номер текущей обрабатываемой вершины.
Трудоемкость алгоритма (6.6), также как процедуры cdeеp (6.5), имеет поря док m, где m – число ребер графа.
Конец примера.
Алгоритм просмотра вширь можно использовать для решения задачи выделения компонент связности графа с такой же трудоемкостью, как и при использовании ал горитма просмотра вглубь. Кроме того, алгоритм просмотра вширь позволяет вычис лять кратчайшие расстояния, измеряемые в числе ребер, от произвольно заданной на чальной вершины графа до всех достижимых вершин. Это позволяет решать многие интересные задачи.
Пример 6.6. Задача поиска кратчайшего пути в лабиринте. Пусть лабиринт задан числовым двумерным массивом L, который соответствует квадратной матрице n×n. Нулевой элемент массива соответствует проходу в лабиринте, а элемент с большим значением (например, 1000) – стене в лабиринте. Из произвольной клетки
лабиринта можно перемещаться (если нет стены) в четырех направлениях: вправо, влево, вверх или вниз. Пусть также задана начальная клетка L[i0,j0] и конечная
клетка L[ik,jk]. На рис. 6.3 показан пример лабиринта, в нем знаком “#” отмече ны клетки со стеной, левая верхняя клетка – начало пути, правая нижняя клетка – ко нец пути.
|
|
|
|
|
|
|
# |
# |
# |
# |
# |
# |
# |
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
# |
|
|
|
# |
|
# |
1 |
# |
|
|
|
# |
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
# |
|
# |
|
|
# |
2 |
# |
# |
|
# |
11 |
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
|
|
|
# |
3 |
4 |
5 |
# |
9 |
10 |
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
4 |
5 |
6 |
7 |
8 |
9 |
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
# |
|
# |
|
|
# |
5 |
# |
# |
8 |
# |
10 |
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
|
|
|
К |
|
# |
6 |
# |
10 |
9 |
10 |
11 |
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
# |
# |
# |
# |
# |
# |
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.3 В этой задаче нет необходимости формировать специальное представление гра
фа, так как матрица L непосредственно сама задает граф. Клетки с нулевым значе нием (на рис. 6.3 клетки с пробелами) задают вершины графа. Каждая из вершин мо жет иметь ребра максимально с четырьмя соседними вершинами (есть ребро или его нет, определяется соседней клеткой). Для облегчения проверок граничных клеток предположим, что массив расширен нулевой и (n+1)–й строкой, а также нулевым и

116
(n+1)–м столбцом, и всем дополнительным элементам присвоено значение, обозна чающее стену. Кроме того, вместо одного массива P будем использовать два масси ва – Pi и Pj, определяющие номер строки и номер столбца клетки. Значение
уровня вершины при работе алгоритма будем записывать непосредственно в массив L (в клетки с нулем). В результате получим следующий алгоритм:
|
|
|
|
Pi[1]:=i0; Pj[1]:=j0; r:=1; t:=1; |
|
||
L[i0,j0]:=1; |
|
|
|
while t<=r do |
|
|
|
begin |
i:=Pi[t]; j:=Pj[t]; q:=L[i,j]+1; |
|
|
if L[i-1,j]=0 then begin |
|
|
|
L[i-1,j]:=q; r:=r+1; Pi[r]:=i-1; Pj:=j |
|
|
|
end; |
|
|
|
if L[i,j-1]=0 then begin |
|
|
|
L[i,j-1]:=q; r:=r+1; Pi[r]:=i; Pj:=j-1 |
|
(6.7) |
|
end; |
|
|
|
if L[i+1,j]=0 then begin |
|
|
|
L[i+1,j]:=q; r:=r+1; Pi[r]:=i+1; Pj:=j |
|
|
|
end; |
|
|
|
if L[i,j+1]=0 then begin |
|
|
|
L[i,j+1]:=q; r:=r+1; Pi[r]:=i; Pj:=j+1 |
|
|
|
end; |
|
|
|
t:=t+1 |
|
|
|
end; |
|
|
|
На рис. 6.3, справа, показан массив L после выполнения алгоритма (6.7). |
|
||
|
|
|
|
k:=L[ik,jk]; i:=ik; j:=jk; |
|
||
while k>0 do |
|
|
|
begin |
Mi[k]:=i; Mj[k]:=j; |
|
|
if L[i-1,j]<L[i,j] then i:=i-1 |
|
(6.8) |
|
else if L[i,j-1]<L[i,j] then j:=j-1 |
|
||
else if L[i+1,j]<L[i,j] then i:=i+1 |
|
|
|
else j:=j+1; |
|
|
|
k:=k-1 |
|
|
|
end; |
|
|
|
Заметим, что трудоемкость алгоритма (6.7) имеет порядок 4∙n2.
По массиву L легко отследить кратчайший путь. Алгоритм (6.8) формирует путь в массивах Mi и Mj с конца. В элементе Mi[k] запоминается номер строки клетки, а в элементе Mj[k] – номер столбца клетки на k–м шаге маршрута. Крат чайший путь может быть не единственным, в этом случае вычисляется один из вари антов кратчайшего пути.
Нетрудно видеть, что количество выполнений цикла в алгоритме (6.8) равно дли не кратчайшего пути.

117
Конец примера.
6.3 Циклы в графе
Циклом в графе называется замкнутый путь, начинающийся в некоторой верши не и проходящий через ряд ребер (дуг) графа, причем ни одно ребро (дуга) не может входить в цикл более одного раза. Если граф неориентированный, то цикл может проходить по ребрам в любом направлении, а если граф ориентированный, то по каждой из входящих в него дуге направление прохода должно совпадать с ориента цией дуги.
С циклами связано большое число различных задач. В частности, эйлеровым на зывается такой цикл, который проходит по всем ребрам (дугам) строго по одному ра зу. При этом по некоторым вершинам эйлеров цикл может пройти несколько раз. За метим, что эйлеров цикл существует не для каждого графа. Интересно, что можно рассматривать задачу построения эйлерова цикла для мультиграфа.
Гамильтонов цикл должен проходить по всем вершинам строго по одному разу, а по ребрам (дугам) – не более одного раза. При этом некоторые ребра (дуги) могут во обще не входить в цикл. Гамильтонов цикл также существует не для каждого графа.
Несмотря на некоторое сходство, задачи построения эйлерова цикла и гамильто нова цикла принципиально различаются. Эйлеров цикл (если он существует) можно построить достаточно эффективно (трудоемкость лучших алгоритмов пропорцио нальна числу ребер). В то же время гамильтонов цикл можно построить в общем слу чае лишь за экспоненциальное время.
Пример 6.7. Алгоритм вычисления эйлерова цикла в ориентированном графе из n вершин. Как известно, эйлеров цикл существует в ориентированном графе, тогда и только тогда, когда в каждую вершину входит ровно столько же ребер, сколько и вы ходит из нее. Поэтому, прежде чем строить цикл, необходимо проверить условия его существования. Если граф задан в виде матрицы смежности, то проверка сводится к тому, что нужно подсчитать количество единиц в i–м столбце и i–ой строке матри цы. Если для всех i = 1, …, n эти количества равны между собой, то эйлеров цикл существует.
Для графа, заданного в виде массива смежных вершин, количество ребер, выхо дящих из вершины i, хранится в элементе массива L[i]. Вычислить количество
ребер, входящих во все вершины, можно алгоритмом (6.9).
for i:=1 to n do R[i]:=0; for i:=1 to n do
for k:=S[i] to S[i]+L[i]-1 do (6.9) begin j:=D[k]; R[j]:=R[j]+1 end
118
Трудоемкость алгоритма (6.9) имеет порядок m, где m – число ребер графа. По
сле выполнения этого алгоритма достаточно попарно сравнить между собой элемен ты массивов L[i] и R[i] для всех i от 1 до n.
Если эйлеров цикл существует, то он, как правило, не единственный. Алгоритм Эйлера вычисляет какой-либо из возможных циклов. В этом алгоритме начальный цикл отслеживается с произвольной, например первой, вершины. Затем просматрива ются все вершины на построенном цикле, и, как только будет обнаружена вершина i, из которой выходит еще не включенная в цикл дуга, отслеживается боковой цикл, который затем вставляется после вершины i.
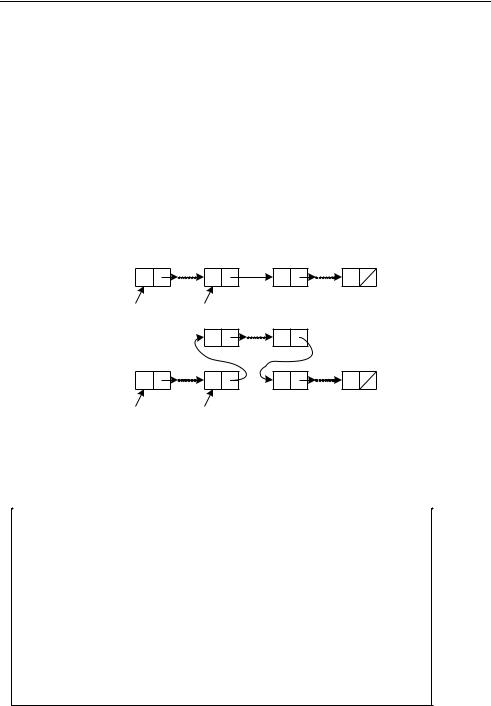
Так как в формируемый цикл многократно вставляются новые фрагменты, то удобнее всего для этого использовать списочные структуры. На рис. 6.4 показано, как в начальный цикл, записанный в линейном списке, вставляется сформированный боковой цикл.
1 |
i |
k |
1 |
pb |
p |
|
|
|
i1 |
i |
|
1 |
i |
k |
1 |
pb |
p |
|
|
Рис. 6.4
Пусть граф задан в виде массива смежных вершин. В алгоритме (6.10) вначале создается список из одного элемента с записанной в него вершиной 1.
|
|
new(p); pb:=p; p^.s:=1; p^.p:=nil; |
|
while p<>nil do |
|
begin |
|
if L[p^.s]>0 then begin |
|
p1:=p^.p; i0:=p^.s; i:=0; p0:=p; |
|
while i<>i0 do |
|
begin new(p2); p^.p:=p2; i:=p^.s; |
(6.10) |
i1:=D[S[i]]; S[i]:=S[i]+1; L[i]:=L[i]-1; |
|
i:=i1; p2^.s:=i; p:=p2 |
|
end; |
|
p^.p:=p1; p:=p0 |
|
end |
|
else p:=p^.p |
|

119
 end;
end;
При отслеживании бокового цикла, как только формируется новый элемент списка, из представления графа удаляется вошедшая в цикл дуга (для этого элемент L[i] уменьшается на 1, а S[i] увеличивается на 1). По окончании формирования боковой цикл в виде отдельного списка вставляется в основной список.
Нетрудно видеть, что трудоемкость алгоритма (6.10) имеет порядок m, где m – число ребер графа.
Конец примера.
Проверка условия существования эйлерова цикла в неориентированном графе сводится к проверке того, что валентность всех вершин графа – четная. В то же время построение в нем эйлерова цикла потребует усложнения алгоритма (6.10). А именно, при удалении из представления графа ребра (i,i1) требуется также удалить ребро (i1,i), для чего придется производить перебор вершин, смежных с i1 (записанных в массиве D). Это не приведет к существенному увеличению трудоемкости всего ал горитма лишь в случае, когда валентность любой вершины графа не превышает константы.
Если не выполняются условия существования эйлерова цикла, то в графе может существовать незамкнутый эйлеров путь, который начинается в одной вершине, а за канчивается в другой. Условие существования эйлерова пути в неориентированном графе следующее: валентности двух вершин нечетные, а всех остальных вершин – четные. Путь начинается в одной из вершин с нечетной валентностью, а заканчавает ся в другой, поэтому в алгоритме первым отслеживается начальный путь между эти ми вершинами. В остальном алгоритм построения пути остается аналогичным алго ритму построения эйлерова цикла.
Условие существования эйлерова пути в ориентированном графе следующее: в одной из вершин i число выходящих дуг на 1 больше числа входящих, а в другой j
– наоборот, число входящих дуг на 1 больше числа выходящих. При этом для каждой из остальных вершин число входящих дуг должно быть равно числу выходящих дуг. При выполнении этого условия эйлеров путь начинается в вершине i и заканчивает ся в вершине j. Изменения в алгоритме (6.10) для поиска эйлерова пути очевидны.
Пример 6.8. Алгоритм вычисления гамильтонова цикла в графе из n вершин. Гамильтонов цикл можно рассматривать как циклическую перестановку вершин гра фа, которая может начинаться с любой вершины, например, первой. Поэтому за осно ву можно взять алгоритм генерации перестановок (4.8), внеся в него следующие из менения:
1)в первой позиции генерируемых перестановок должно быть записано 1;
2)очередную вершину следует включать в перестановку только в том случае, если из предыдущей вершины до нее есть ребро (дуга);
3)перед включением последней вершины должно проверяться наличие ребра (дуги) между последней и первой вершинами.

120
Пусть граф задан в виде матрицы смежности. Генерируемые циклы будем запи сывать в массиве P. Так же как в алгоритме (4.8), в массиве R. будем отмечать чис
ла (номера вершин), вошедшие в перестановку (цикл). Тогда модифицированный ал горитм будет следующим:
procedure hamilton(k:integer); var i,j:integer;
begin i:=P[k-1]; for j:=1 to n do
if (R[j]=0)and(M[i,j]=1) then begin
P[k]:=j; R[j]:=1;
if k=n then begin (6.11) if M[j,1]=1 then ВЫВОД
end
else hamilton(k+1);
R[j]:=0 end;end
Вначале в первые элементы массивов P и R должны быть записаны единицы, а
во все остальные элементы R – нули. После этого процедура вызывается оператором hamilton(2). Алгоритм (6.11) генерирует все возможные гамильтоновы циклы,
но его нетрудно изменить так, чтобы он генерировал только один цикл (если тот су ществует). К сожалению, для проверки существования гамильтонова цикла нет дру гого способа, кроме того, как попытаться его построить.
Трудоемкость алгоритма (6.11) в худшем случае аналогична трудоемкости алго ритма генерации перестановок (4.8).
Заметим также, что для алгоритма (6.11) совершенно неважно, ориентированный граф или нет, в обоих случаях алгоритм будет работать правильно.
Конец примера.
Если в графе не существует гамильтонов цикл, то в нем может существовать не замкнутый гамильтонов путь, для отыскания которого в алгоритм (6.11) требуется
внести следующие изменения:
1) в процедуре hamilton убрать проверку наличия ребра (дуги) между послед
ней и первой вершинами пути;
2) вызов процедуры hamilton необходимо производить внутри цикла, в кото ром первый элемент массива P поочередно принимает значения от 1 до n.
Это необходимо для проверки всех возможных вариантов начала гамильтонова пути, который может начинаться с любой вершины графа, причем проверки замыка ния пути не требуется.
