
- •§14. Строение линейных открытых множеств на r
- •§ 15. Строение линейных замкнутых множеств на r
- •§15. Строение линейных совершенных множеств
- •§16. Канторово множество
- •§17. Мера ограниченного открытого множества на r Определение меры ограниченного открытого множества
- •Свойства мер открытых ограниченных множеств
- •§18. Мера ограниченного замкнутого множества Определение меры ограниченного замкнутого множества
- •Свойства мер ограниченных замкнутых множеств
- •§19. Лемма Гейне-Бореля. Компактные множества
§16. Канторово множество
Вопросы для самостоятельного изучения:
Построение Канторова множества
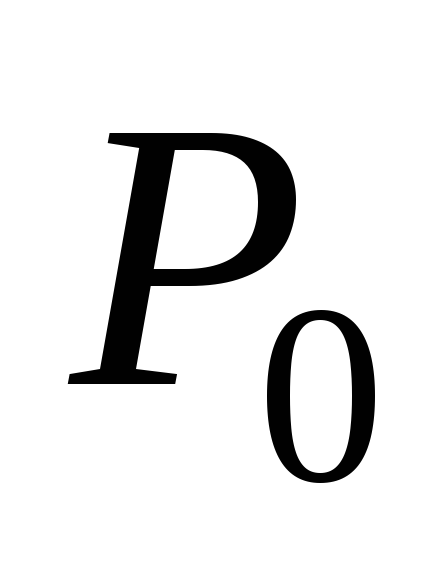 .
.Свойства:
а) совершенное множество;
б) нигде не плотно в R;
в)
![]() .
.
§17. Мера ограниченного открытого множества на r Определение меры ограниченного открытого множества
Определение 1. Мерой интервала (a,b), a<b,называется его длина, то есть числоm=m(0,1)=a-b.
Из определения следует, что m(a,b)>0.
Всякое открытое множество является
объединением конечного числа или
счетного множества попарно непересекающихся
интервалов, концы которых не принадлежат
G(составляющих
интервалов). ПустьG– ограниченное открытое множество и![]() =,
=,![]() .
Так какG– ограниченное
множество, то
.
Так какG– ограниченное
множество, то![]() ,
мера которогоm=a-b.
Очевидно, что
,
мера которогоm=a-b.
Очевидно, что![]() .
Итак, интервалы
.
Итак, интервалы![]() попарно не пересекаются попарно и
содержатся в интервале (a,b).
попарно не пересекаются попарно и
содержатся в интервале (a,b).
Рассмотрим два случая:
1. Пусть G– конечное
объединение интервалов![]() .
Ясно, что
.
Ясно, что![]() (1) (сумма мер интервалов - положительное
число).
(1) (сумма мер интервалов - положительное
число).
2. Пусть G– счётное
объединение интервалов![]() .
Рассмотрим ряд (2)
.
Рассмотрим ряд (2)![]() - положительный числовой ряд. Рассмотрим
частичные суммы ряда
- положительный числовой ряд. Рассмотрим
частичные суммы ряда![]() .
Так как ряд (2) – положительный, то
.
Так как ряд (2) – положительный, то![]() - возрастающая последовательность, на
основании (1) она ограничена, следовательно,
- возрастающая последовательность, на
основании (1) она ограничена, следовательно,![]() ,
тогда по определению ряд (2) сходится и
его сумма есть неотрицательное число:
,
тогда по определению ряд (2) сходится и
его сумма есть неотрицательное число:
![]() .
(3)
.
(3)
Из (1) и (3) следует, что если G- открытое ограниченное множество, то сумма мер его составляющих интервалов неотрицательное число, не большее (b-a).
Определение 2.
Мерой ограниченного
открытого множества Gназывается
сумма мер его составляющих интервалов,
то есть если![]() ,
то
,
то![]() .
.
Ясно, что
![]() .
.
Свойства мер открытых ограниченных множеств
Теорема 1.
Если ограниченное открытое множествоGявляется объединением
конечного числа или счетного множества
попарно непересекающихся открытых
множествGk,
то мера множестваGравна сумме мер множествGk,
то есть![]() .
.
Доказательство:
Возьмём
![]() ,
,![]() .
Тогда
.
Тогда![]() .
В правой части последнего равенства не
более чем счетное число интервалов. Так
как
.
В правой части последнего равенства не
более чем счетное число интервалов. Так
как![]() не пересекаются попарно, то и интервалы
в последнем равенстве попарно не
пересекаются, следовательно, они являются
составляющими интервалами для множестваG.По определению
2
не пересекаются попарно, то и интервалы
в последнем равенстве попарно не
пересекаются, следовательно, они являются
составляющими интервалами для множестваG.По определению
2![]() .
.
Теорема 2.
Пусть![]() - ограниченные открытые множества, такие
что
- ограниченные открытые множества, такие
что![]() .
Тогда
.
Тогда![]() .
.
Доказательство:
Пусть
![]() .
Возьмем любой составляющий интервал
множества
.
Возьмем любой составляющий интервал
множества![]() ,
для него в силу условия
,
для него в силу условия![]() обязательно существует такой составляющий
интервал
обязательно существует такой составляющий
интервал![]() ,
что
,
что![]()
![]()
![]() ,
тогда
,
тогда![]() .
Просуммируем все такие неравенства:
.
Просуммируем все такие неравенства:![]() .
Таким образом,
.
Таким образом,![]() .
.
§18. Мера ограниченного замкнутого множества Определение меры ограниченного замкнутого множества
Определение 1. Мерой пустого множестваназывается число 0:т(Ø)=0.
Пусть F- ограниченное
замкнутое множество. Тогда существует
наименьший отрезок![]()
![]() ,
содержащий множествоF.
Рассмотрим множество
,
содержащий множествоF.
Рассмотрим множество![]() .
Оно ограничено, так как содержится в
.
Оно ограничено, так как содержится в![]() ,
и открыто как дополнение замкнутого
множества. Следовательно, существует
мера этого множества
,
и открыто как дополнение замкнутого
множества. Следовательно, существует
мера этого множества![]() .
Так как
.
Так как![]() то по теореме 2
то по теореме 2![]() .
Тогда
.
Тогда![]() .
.
Определение 2:
Мерой ограниченного
замкнутого множества Fназывается
число, обозначаемоеmFи определяемое по формуле![]() ,
где
,
где![]() - наименьший отрезок, содержащий множествоF.
- наименьший отрезок, содержащий множествоF.
mF– неотрицательное число.
