Тема 18
1.Понятие первообразной ф н ции
2.Основное свойство первообразной ф н ции
3.Криволинейная трапеция и ее площадь
4.Форм ла Ньютона—Лейбница
5.Основные правила инте(рирования
6.Вычисление площадей с помощью инте(рала
СПРАВОЧНЫЙ МАТЕРИАЛ
1. Понятие первообразной ф н ции
1°. Под дифференцированием фун ции f(x) мы понимаем нахождение производной f′(x).
Например, если f(x) = cos 2x, то f′(x) = –sin 2x · (2x)′ = –2 sin 2x для всех x Ý R.
2°. Нахождение фун ции f(x) по заданной ее производной f′(x) называют операцией инте рирования.
3°. Та им образом, операция инте#рирования обратна операции дифференцирования. Следовательно, операция инте#рирования состоит в том, что по заданной производной f′(x) находят (восстанавливают) фун цию f(x).
4°. Например, пусть f′(x) = 4x3. Следует найти f(x). Опираясь на правило дифференцирования, нетрудно установить, что f(x) = x4. Ле# о до#адаться, что f(x) находится неоднозначно.
5°. В ачестве f(x) можно взять и та ие фун ции, а f(x) = = x4 + 2, f(x) = x4 – 5, f(x) = x4 + 
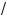 5 и др., пос оль у производная
5 и др., пос оль у производная
аждой из данных фун ций равна 4x3. Все эти фун ции отличаются дру# от дру#а толь о постоянным сла#аемым.
6°. Общее решение задачи можно записать в виде f(x) = x4 + C, #де C — произвольное действительное число. Любую из найденных фун ций f(x) называют первообразной для фун ции f′(x) = 4x3.
7°. Фун цию F называют первообразной для фун ции f на заданном промежут е, если для всех x из это#о промежут а F′(x) = f(x).




 6 – 2x )
6 – 2x )

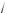 2 ; б) a Ý (–×; 3); в) a Ý (31; +×); ) a Ý (1; 16). 7. а) 1,5; б) –4. 8. а) –7; б) –4. 9. y Ý (–×; –1) Ÿ (1; +×). 10. Если a < 3, то
2 ; б) a Ý (–×; 3); в) a Ý (31; +×); ) a Ý (1; 16). 7. а) 1,5; б) –4. 8. а) –7; б) –4. 9. y Ý (–×; –1) Ÿ (1; +×). 10. Если a < 3, то
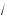 16 + a
16 + a
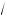 16 + a
16 + a

 5 и др., пос оль у производная
5 и др., пос оль у производная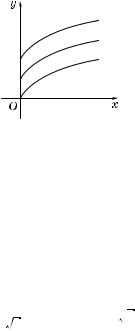






 2πn , n = 0, 1, 2, ... .
2πn , n = 0, 1, 2, ... .