2. Та им образом, требуется найти все значения a, при оторых системе неравенств
(a – 5)x2 + 4x + (a – 5) m 0, |
(2) |
ax2 + 4x + a > 0 |
(3) |
удовлетворяет любое значение x.
а) При a = 5 неравенство (2) примет вид 4x m 0; оно не выполняется, например, для x = 1.
б) При a = 0 неравенство (3) примет вид 4x > 0; оно не выполняется, например, для x = –1.
в) Пусть a > 5. Рассмотрим неравенство (2). Если x = 0, то оно примет вид a – 5 m 0. Это означает, что при любом a > 5 значение x = 0 не является решением системы (2), (3), а следовательно, и исходно#о неравенства (1).
#) Пусть a < 0. Рассмотрим неравенство (3). Если x = 0, то оно примет вид a > 0, что противоречит неравенству a < 0. Поэтому при a < 0 значение x = 0 не является решением системы (2), (3), а следовательно, и исходно#о неравенства.
д) Пусть 0 < a < 5. То#да вадратный трехчлен (a – 5)x2 + 4x + + (a – 5) неположителен для любо#о x, если е#о дис риминант D1 =
= 16 – 4(a – 5)2 неположителен. Квадратный трехчлен ax2 + 4x + a положителен для любо#о x, если е#о дис риминант D2 = 16 – 4a2
отрицателен.
4. Та им образом, задача сводится решению системы
0 < a < 5,
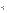 16 – 4(a – 5)2 m 0,
16 – 4(a – 5)2 m 0,
16 – 4a2 < 0.
Та а
0 < a < 5, |
|
0 < a < 5, |
|
–4 + (a – 5)2 l 0, _ |
|
(a – 7)(a – 3) l 0, _ |
a2 – 4 > 0 |
|
(a – 2)(a + 2) > 0 |
0 < a < 5,
_  a – 3 m 0, _ 2 < a m 3, a – 2 > 0
a – 3 m 0, _ 2 < a m 3, a – 2 > 0
то исходное неравенство справедливо для всех x при значениях a из промежут а 2 < a m 3.
5. Ответ: a Ý (2; 3].





 5(x
5(x ax
ax
 16 – 4(a – 5)
16 – 4(a – 5) a – 3
a – 3 

 7 и a
7 и a 
 7 .
7 .
 7 ]
7 ] 
 7 ; +
7 ; + x – a
x – a 


 b
b
 b
b

 b
b
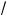 2 . При этих значениях параметра b система (3), (4) имеет решение
2 . При этих значениях параметра b система (3), (4) имеет решение
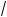 b
b
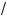 2 , то
2 , то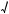 b
b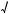 b
b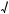
 b
b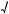 b
b
