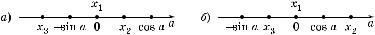Задачи с параметрами и методы их решения

16. При а их значениях a прямая 4x + y – 5 = 0 является аса-

2a

=------ – 1 в точ е x0 имеет вид x2

3. Чтобы уравнение (1) совпало с уравнением y = –4x + 5, требуется выполнение условий

4a

–------ = –4,

x30

6a

(2)

------ – 1 = 5.

x20

4. Решив систему (2), находим x0 = 1, a = 1.

5. Ответ: a = 1.

17. При а ом наименьшем натуральном k уравнение x3 + 3x2 – 45x + k = 0

имеет ровно один орень?

1. Построим эс из #рафи а фун ции y1 = x3 + 3x2 – 45x и определим наименьшее натуральное значение k, при отором этот #рафи пересе ает прямую y2 = –k ровно в одной точ е.

#) y1(–5) = 175; y1(3) = –81;

261

Рис. 91

Рис. 92

д) изменение зна ов производной y′ в интервалах (–×; –5),

1

(–5; 3) и (3; +×) иллюстрирует рис. 91. На рис. 92 дано схематиче- с ое изображение #рафи а фун ции y1.

3.Очевидно, что данное уравнение имеет единственное решение, если –k > 175 или –k < –81, т. е. k < –175 или k > 81. Наименьшее натуральное значение k равно 82.

4.Ответ: k = 82.

18.При а ом значении параметра a минимум фун ции

равен 1?

1. Найдем производную данной фун ции:

f′(x) = (ax2 – 6ax + a2 – 9)′ = 2ax – 6a.

2. Пола#ая f′(x) = 0, имеем 2ax – 6a = 0, от уда a − 0, x = 3.

262

3. Найдем значение фун ции (1) в точ е x = 3:

4.Решив уравнение (2), получим a1 = –1; a2 = 10.

5.Та а по условию требуется определить минимум фун ции, то ветви параболы (1) направлены вверх, а это значит, что a2 = 10.

6.Ответ: a = 10.

19.При а ом значении параметра a минимум фун ции

f(x) = –2x3 + 3x2 + 12x + 4a

равен 1?

1. f′(x) = –6x2 + 6x + 12.

2. y′ = 0 при x1 = –1; x2 = 2.

19

3. y(2) = 20 + 4a = 1; a1 = –------ .

4

4. y(–1) = –7 + 4a = 1; a2 = 2.

5. Схематичес ое изображение #рафи а фун ции (рис. 93) по азывает, что ее минимум дости#ается в точ е x1 = –1;

6.Ответ: a = 2.

20.Найти множество значений параметра k, при оторых асательная параболе

263

4. Запишем уравнение асательной параболе (1):

Эта асательная должна быть та же асательной параболе (2). 5. Чтобы найти общие точ и асательной (3) и параболы (2), со-

ставим уравнение

(k – 4)x + k – 1 = x2 – 6x + 5, или x2 – (k + 2)x + 6 – k = 0. (4)

6.Та а прямая (3) является асательной ривой (2), то она имеет единственную общую точ у с этой ривой.

7.Уравнение (4) имеет единственное решение, если дис риминант это#о уравнения равен нулю, т. е. D = 0.

8.Из равенства D = (k + 2)2 – 4(6 – k) = 0 находим k1 = –10,

k2 = 2.

9.Ответ: k Ý {–10; 2}.

21.При а ом значении параметра a хорда параболы

в точ е с абсциссой x0 = 2, делится этой точ ой пополам?

тельной ривой (2) в точ е M(2; –1) имеет вид y = x – 3.

2.Пусть эта асательная пересе ает параболу (1) в точ ах A

иB; то#да абсциссы этих точе являются орнями уравнения

3.Точ а M есть середина отрез а AB, поэтому ее абсцисса равна полусумме абсцисс точе A и B.

4.Перепишем уравнение (3) в виде

264

7. Подставив значение a = 1 в выражение (5), замечаем, что D > 0, поэтому a = 1 удовлетворяет требованию задачи.

удовлетворяет.

9.Ответ: a = 1.

22.При а ом значении параметра a асательная #рафи у фун -

ции y = a – x2 отсе ает от I четверти равнобедренный треу#ольни

9

с площадью, равной ------ ?

32

1.Уравнение асательной #рафи у фун ции y = f(x) в точ е M(x0; y0) имеет вид y – y0 = f′(x0)(x – x0), #де f′(x0) = tg α, α — у#ол на лона асательной оси абсцисс.

2.Та а по условию асательная #рафи у данной фун ции отсе ает от I четверти равнобедренный треу#ольни , то α = 135° и, значит, f′(x0) = –1.

ной #рафи у данной фун ции запишется та :

1 y = –x + a + -- .

4

5.Эта асательная пересе ает оси оординат в точ ах A 0; a + 1

--4

иB a + 1 ; 0 .

--

4

265

6. Со#ласно условию, точ и A и B лежат на положительных по-

23. При а ом значении параметра a прямые, проходящие через точ у M(1; 1) плос ости xOy и асающиеся двух ветвей #иперболы

4. При a < 0 уравнение (2) имеет два орня t1 и t2, оторые являются абсциссами точе A и B соответственно. По теореме Виета t1 + t2 = 2a, t1t2 = a.

266

5.Пос оль у ветви рассматриваемой #иперболы симметричны относительно прямой y = x, а точ а M(1; 1) лежит на этой прямой, точ и A и B симметричны относительно прямой y = x.

6.Та им образом, если точ а A имеет оординаты (t1; t2), то точ-

а B будет иметь оординаты (t2; t1). Отсюда следует, что MA = MB

при любом a < 0.

7. Найдем MA2 и AB2. С учетом полученных выше соотношений между орнями t1 и t2 имеем

MA2 = (t1 – 1)2 + (t2 – 1)2 = 4a2 – 6a + 2,

AB2 = (t1 – t2)2 + (t2 – t1)2 = 8a2 – 8a.

8. Со#ласно условию, треу#ольни MAB правильный, поэтому MA = AB, т. е.

4a2 – 6a + 2 = 8a2 – 8a.

1

Решив это уравнение с учетом то#о, что a < 0, получим a = –-- .

2

9. Найдем площадь треу#ольни а MAB:

S = 1 · MA · AB · sin 60° = 1 · AB2 · 3 = 3 3 .

-- -- ------- ----------

2 2 2 2

1 3 3

10. Ответ: a = –-- ; S = ---------- .

2 2

24. Найти все значения параметра a, удовлетворяющие неравенст-

π

вам 0 m a m -- , при аждом из оторых минимум фун ции

2

f(x) = 3x4 + 4x3(cos a – sin a) – 3x2 sin 2a

на отрез е –sin a m x m cos a принимает наименьшее значение.

1.Обозначим через ϕ(a) наименьшее значение фун ции f(x) на отрез е [–sin a; cos a] при фи сированном a.

2.Имеем

f′(x) = 12x3 + 12x2(cos a – sin a) – 6x sin 2a.

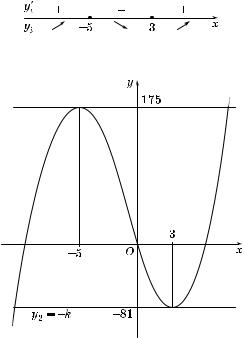
3. Решив уравнение f′(x) = 0, находим орни производной: x1 = 0, x2 = sin a, x3 = –cos a.

267

Рис. 94

4. Рассмотрим два случая.

π

а) Если 0 m a m -- , то sin a m cos a и по отношению отрез у

4

[–sin a; cos a] орни x1, x2, x3 расположатся та , а по азано на рис. 94, а. Изменение зна ов производной иллюстрирует следующая таблица:

Отсюда следует, что ϕ(a) = min {f(–sin a); f(x2)}. Но

f(x2) – f(–sin a) = f(sin a) – f(–sin a) = 8 sin3 a (cos a – sin a) l 0.

Значит,

ϕ(a) = f(–sin a) =

=3 sin4 a – 4 sin3 a (cos a – sin a) – 6 sin3 a cos a =

=7 sin4 a – 10 sin3 a cos a.

[–sin a; cos a] расположение орней производной будет та им, а по азано на рис. 94, б. Изменение зна ов производной иллюстрирует таблица:

Следовательно, ϕ(a) = min {f(x3); f(cos a)}. Но

f(x3) – f(cos a) = f(–cos a) – f(cos a) = –8 cos3 a (cos a – sin a) l 0.

Значит,

ϕ(a) = f(cos a) =

=3 cos4 a + 4 cos3 a (cos a – sin a) – 6 sin a cos3 a =

=7 cos4 a – 10 sin a cos3 a.

268

5. Ита ,

статочно найти минимум фун ции ϕ(a) = 7 sin4 a – 10 sin3 a cos a на

6. Имеем

ϕ′(a) = 28 sin3 a cos a – 30 sin2 a cos2 a + 10 sin4 a = = 2 sin2 a cos2 a (5 tg2 a + 14 tg a – 15).

Все орни производной ϕ′(a), принадлежащие промежут у 0 <

tg a положительны и не превосходят 1; поэтому находим единственный орень производной ϕ′(a), удовлетворяющий неравенствам

269

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1.При а ом значении a прямая y = a + x ln 81 является асательной #рафи у фун ции f(x) = 9x + 2 · 3x + 1 – x ln 81?

2.Установить, при а их значениях a прямая:

а) 3ax + y = a2x + 7 параллельна асательной ривой 3x2 +

2a

+------ + y = 0, проведенной в точ е x = 1; x

б) 4a2x – y = 15ax – 9 параллельна асательной ривой 4a –

------

x3

– y + x = 0, проведенной в точ е x = –1;

в) 2 – 3ax = 4a2x – y параллельна асательной ривой x5 –

------

10

4a

–y + ------ = 0, проведенной в точ е x = –2. x

Вответе у азать наименьшее значение a.

3. Установить, при а их значениях a асательная ривой:

а) x3 – 4a + y = 0, проведенная в точ е x = 2, параллельна пря-

------

x2

мой 8ax – 5 = a2x – y;

б) 27a – y – 2x2 = 0, проведенная в точ е x = 3, параллельна

----------

x2

прямой 10ax + y = a2x + 6;

в) x3 + y – 3a = 0, проведенная в точ е x = –1, параллельна

------

x4

прямой 4a2x – y = 7 – 5ax.

В ответе у азать наибольшее значение a.

4. Найти значение b, при отором наименьшее значение фун - ции:

а) y – x3 + 27x + 3b на отрез е [2; 5] равно 1;

б) y = –4x3 + 48x – 2b на отрез е [–4; –1] равно (–60).

270