Задачи с параметрами и методы их решения

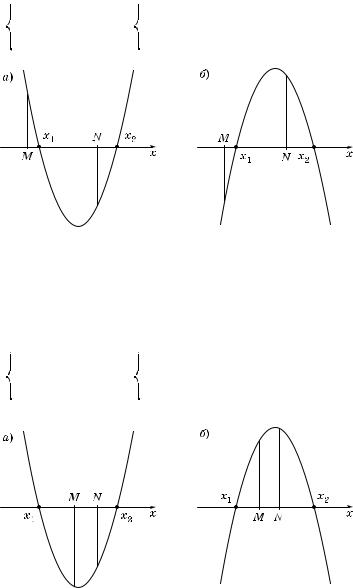
8°. С л е д с т в и е 3. Чтобы толь о меньший орень вадратно о трехчлена лежал в интервале (M; N), необходимо и достаточно выполнение условий (рис. 44, а и б):

Рис. 44

9°. С л е д с т в и е 4. Чтобы один орень вадратно о трехчлена был меньше, чем M, а дру ой больше, чем N (M < N), т. е. отрезо [M; N] цели ом лежал внутри интервала между орнями, необходимо и достаточно выполнение условий (рис. 45,

а и б):

Рис. 45

151

ЗАДАЧИ С РЕШЕНИЯМИ

1. При а их значениях параметра k орни вадратно#о уравнения (k + 2)x2 + 2kx + k – 4 = 0

имеют разные зна и?

1. Та а степень уравнения равна 2, то k + 2 − 0.

2. Уравнение имеет два различных орня при условии D = k2 –

----

4

– (k + 2)(k – 4) > 0, причем произведение орней отрицательно:

k – 4 x1x2 = ------------ < 0.

k + 2

3. Ита , приходим системе неравенств

k + 2 − 0,

k2 – (k + 2)(k – 4) > 0,

k – 4

------------ < 0. k + 2

4. Решив эту систему, получим –2 < k < 4. 5. Ответ: k Ý (–2; 4).

2. Найти все значения параметра a, при оторых орни уравнения (a – 2)x2 – 2ax + 2a – 3 = 0 (1)

действительны, и определить зна и орней.

1.Пусть a = 2; то#да уравнение (1) является линейным и имеет один орень, равный 0,25.

2.Пусть a − 2; то#да уравнение (1) имеет действительные орни, если дис риминант вадратно#о трехчлена неотрицателен, т. е.

----

D = a2 – (a – 2)(2a – 3) l 0,

4

от уда, учитывая, что a − 2, находим

1 m a < 2, 2 < a m 6. (2)

3. Для определения зна ов орней воспользуемся теоремой Виета:

152

4. Корни имеют одина овые зна и, если их произведение положительно. Если при этом положительна и сумма орней, то оба они положительны. Та им образом,

от уда с учетом неравенств (2) находим 2 < a m 6.

5. Если произведение орней положительно, а их сумма отрицательна, то оба орня отрицательны. Значит,

от уда с учетом неравенств (2) находим 1 m a < 1,5.

6. Если орни имеют разные зна и, то произведение орней отрицательно и выполняется неравенство

2a – 3 x1x2 = ---------------- < 0

a – 2

от уда с учетом неравенств (2) находим 1,5 < a < 2.

7. Если хотя бы один из орней уравнения равен нулю, то

2a – 3

x1x2 = ---------------- = 0, от уда следует, что a = 1,5. Та а при a = 1,5 a – 2

сумма орней отрицательна, то дру#ой орень отрицателен. 8. Ответ: орни уравнения действительны при 1 m a m 6;

если 2 < a m 6, то оба орня положительны; если a = 2, то один положительный орень; если 1,5 < a < 2, то орни имеют разные зна и;

если a = 1,5, то один из орней равен нулю, а дру#ой отрицателен;

если 1 m a < 1,5, то оба орня отрицательны.

3. В зависимости от значений параметра p исследовать зна и орней уравнения

(p + 2)x2 – 2(p + 3)x + p + 5 = 0.

1. Со#ласно теореме Виета, для орней вадратно#о уравнения

153

2. Пусть x1 > 0, x2 > 0; то#да получим систему

Решив эту систему (рис. 46, а), находим p Ý (–×;–5) Ÿ (–2; –1). 3. Пусть x1 < 0, x2 < 0; то#да получим систему

Эта система не имеет решений (рис. 46, б).

4. Пусть x1 > 0, x2 < 0, x1 > |x2|; то#да получим систему

Решив эту систему (рис. 46, в), находим p Ý (–5; –3). 5. Пусть x1 > 0, x2 < 0, x1 < |x2|; то#да получим систему

Решив эту систему (рис. 46, ), находим p Ý (–3; –2). 6. Ответ: x1 > 0, x2 > 0 при p Ý (–×; –5) Ÿ (–2; –1);

x1 > 0, x2 < 0, x1 > |x2| при p Ý (–5; –3); x1 > 0, x2 < 0, x1 < |x2| при p Ý (–3; –2); случай x1 < 0, x2 < 0 невозможен.

154

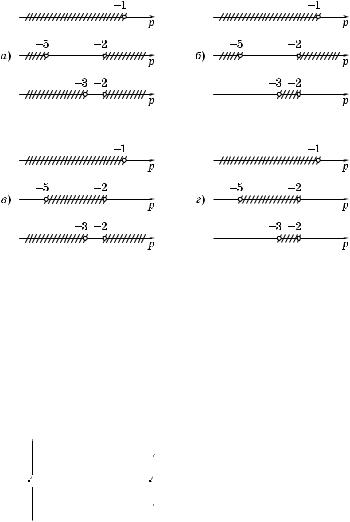
Рис. 46

4. Найти все значения параметра c, при оторых оба орня вадратно#о уравнения

x2 + 4cx + 1 – 2c + 4c2 = 0

действительны и меньше, чем (–1).

1.Здесь a = 1 > 0.

2.Применяя теорему 1 из п. 2, составим систему

f(–1) > 0,

3.Решив систему (1), находим c > 1.

4.Ответ: c Ý (1; +×).

5.Найти все значения параметра k, при оторых оба орня вадратно#о уравнения

x2 – 6kx + 2 – 2k + 9k2 = 0

действительны и больше 3.

155

1.Здесь a = 1 > 0.

2.Применяя теорему 2 из п. 2, получаем систему неравенств

f(3) > 0,

6. При а их значениях параметра k один из орней уравнения

(k2 + k + 1)x2 + (2k – 3)x + k – 5 = 0

больше 1, а дру#ой меньше 1?

1.Здесь a = k2 + k + 1 > 0 при всех k.

2.Со#ласно теореме 3 из п. 2, имеем f(1) < 0, т. е.

3. Решив неравенство (1), находим

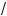–2 – 11 < k < –2 + 11 .

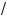4.Ответ: k Ý (–2 – 11 ; –2 + 11 ).

7.При а их значениях параметра m орни уравнения

x2 – 2(m + 2)x + m2 + 12 = 0

принадлежат отрез у [–1; 4]?

1. Ветви параболы y = x2 – 2(m + 2)x + m2 + 12 направлены вверх (та а a = 1 > 0). Эта парабола должна иметь:

а) точ и пересечения с осью абсцисс;

b

б) вершину с абсциссой –------ , принадлежащей отрез у [–1; 4];

2a

в) неотрицательные ординаты f(4) и f(–1). 2. У азанным требованиям отвечает рис. 47.

156

3. Со#ласно следствию 1 из п. 2, запишем и решим систему неравенств

D

---- l 0,

4

b

–1 m –------ m 4,

2a f(4) l 0,

f(–1) l 0,

Рис. 47

т. е.

(m + 2)2 – m2 – 12 l 0, –1 m m + 2 m 4,

16 – 8(m +2) + m2 + 12 l 0, 1 + 2(m + 2) + m2 + 12 l 0.

4. Ответ: m = 2.

8. При а их значениях параметра k орни уравнения

kx2 – (k + 1)x + 2 = 0

будут действительными и оба по абсолютной величине меньше 1?

1.Корни уравнения должны быть действительными и удовлетворять условиям – 1 < x1 < 1 и –1 < x2 < 1.

2.Со#ласно следствию 1 из п. 2, получаем сово упность двух систем неравенств для нахождения параметра k:

157

3.Решив систему а), находим k l 3 + 22 . Система б) не имеет решений.

4.Ответ: k Ý [3 + 2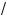2 ; +×).

9.При а их значениях параметра p больший орень уравнения

px2 + (2p – 7)x – 10p = 0 принадлежит интервалу (4; 6)?

1.Для то#о чтобы выполнялись требования задачи, нужно, чтобы #рафи вадратно#о трехчлена f(x) = px2 + (2p – 7)x – 10p имел вид, изображенный на рис. 48, а или на рис. 48, б.

2.Со#ласно следствию 2 из п. 2, получаем сово упность двух систем неравенств:

Рис. 48

158

10. При а их значениях параметра p меньший орень уравнения

(1 – p)x2 – (3p – 8)x + p2 – 1 = 0 по модулю меньше 1?

1.По условию меньший орень уравнения должен принадлежать интервалу (–1; 1).

2.Поэтому вадратный трехчлен f(x) = (1 – p)x2 – (3p – 8)x +

+p2 – 1 должен иметь вид, изображенный на рис. 49, а или на рис. 49, б.

3.Воспользуемся следствием 3 из п. 2 и запишем сово упность двух систем неравенств:

4.Система а) не имеет решений, а из системы б) находим, что 1 < p < 2.

5.Ответ: p Ý (1; 2).

Рис. 49

159

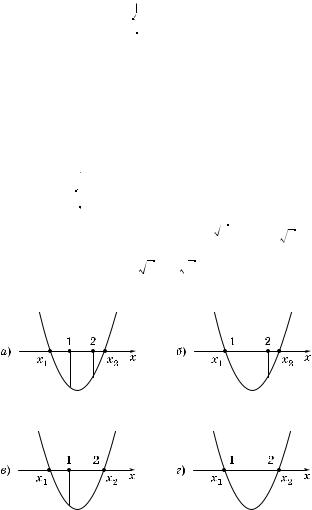
11. При а их значениях k неравенство x2 + kx + k2 + 6k < 0 выполняется для всех 1 < x < 2?

1. Чтобы неравенство x2 + kx + k2 + 6k < 0 имело место для всех 1 < x < 2, т. е. чтобы интервал (1; 2) лежал между орнями вадратно#о трехчлена f(x) = x2 + kx + k2 + 6k, нужно, чтобы выполнялись требования следствия 4 из п. 2:

f(1) m 0, f(2) m 0.

2. Отметим, что здесь записаны нестро#ие неравенства, пос оль-у возможно не толь о расположение параболы, у азанное на рис. 50, а, но и расположения, изображенные на рис. 50, б— . В последних трех случаях один или оба орня вадратно#о трехчлена мо#ут совпадать с точ ами x1 = 1 или x2 = 2, но внутренние точ и интервала между орнями удовлетворяют неравенству 1 < x < 2.

3. Ита , имеем систему неравенств

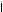f(1) = 1 + k + k2 + 6k m 0, f(2) = 4 + 2k + k2 + 6k m 0.

Рис. 50

160