
- •Геометрический смысл модуля и аргумента производной
- •1. Сохранение угла между кривыми
- •2. Постоянство растяжений
- •3. Определение конформного отображения
- •1. Линейная функция
- •2. Дробно-линейная функция
- •3. Функция Жуковского
- •4. Функция
- •5. Тригонометрические функции и
- •6. Гиперболические функции и
5. Тригонометрические функции и
Тригонометрические функции в комплексной
области просто выражаются через
показательную функцию. По формуле Эйлера
имеем:
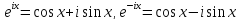 ,
откуда
,
откуда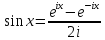 ,
,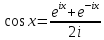 .
.
Учитывая это, примем по определению для
любого комплексного
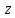
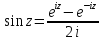 ,
,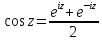 . (3.2.1)
. (3.2.1)
Отметим, что функции (3.2.1) периодичны с
периодом
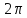 .
.
Рассмотрим функция
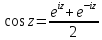 .
Эту функцию можно представит в виде
суперпозиции функций:
.
Эту функцию можно представит в виде
суперпозиции функций:
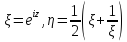 (3.25.2)
(3.25.2)
В силу периодичности функции
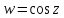 ,
она не является однолистной на всей
комплексной плоскости
,
она не является однолистной на всей
комплексной плоскости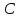 .
Можно разбить комплексную плоскость
.
Можно разбить комплексную плоскость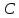 на счетное число областей
на счетное число областей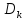 – вертикальные полосы:
– вертикальные полосы: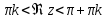 (рис.3.2.1).
(рис.3.2.1).
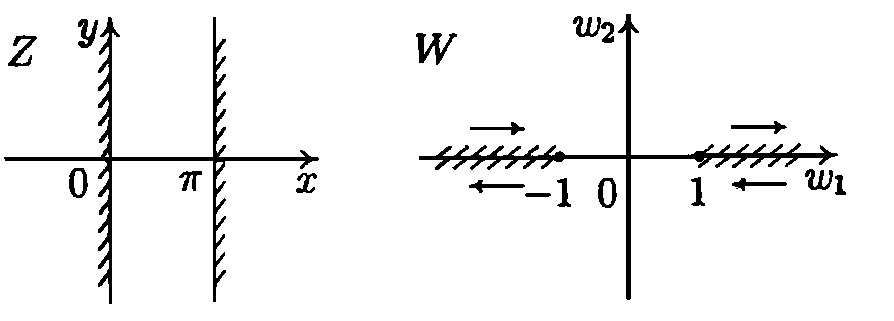
Рисунок 3.2.1.
Функция
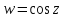 каждую
область
каждую
область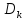 kпереводит на всю комплексную плоскость
kпереводит на всю комплексную плоскость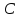 с двумя выброшенными лучами:
с двумя выброшенными лучами: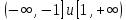 .
.
Если рассмотреть нижнюю полуполосу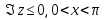 ,
то функция
,
то функция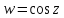 переводит ее на верхнюю полуплоскость
переводит ее на верхнюю полуплоскость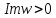 .
.
Рассмотрим функцию
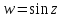 .
Полагая, что
.
Полагая, что
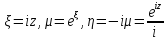 (3.2.3)
(3.2.3)
получим:
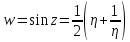 . (3.2.4)
. (3.2.4)
То есть отображение
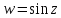 можно рассматривать как суперпозицию
уже рассмотренных отображений.
можно рассматривать как суперпозицию
уже рассмотренных отображений.
Найдем условия его однолистности. Пусть
область
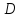 при отображениях (3.2.3) переходит
последовательно в
при отображениях (3.2.3) переходит
последовательно в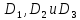 .
Первое и третье из отображений (3.2.3)
однолистны всюду. Для однолистности
второго необходимо и достаточно, чтобы
.
Первое и третье из отображений (3.2.3)
однолистны всюду. Для однолистности
второго необходимо и достаточно, чтобы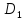 не содержало ни одной пары точек
не содержало ни одной пары точек ,
для которых
,
для которых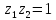 .
Переходя с помощью формул (3.2.3) к плоскости
.
Переходя с помощью формул (3.2.3) к плоскости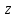 ,
получим, что для однолистности (3.2.4) в
области
,
получим, что для однолистности (3.2.4) в
области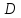 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы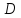 не содержало ни одной из точек
не содержало ни одной из точек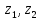 ,
для которых, с одной стороны
,
для которых, с одной стороны
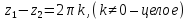 (3.2.5)
(3.2.5)
и с другой
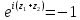 или
или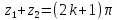 (3.2.6)
(3.2.6)
Этим условиям удовлетворяет, например,
полуполоса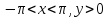 .Последовательные
этапы её отображения изображены на рис.
3.2.2.
.Последовательные
этапы её отображения изображены на рис.
3.2.2.
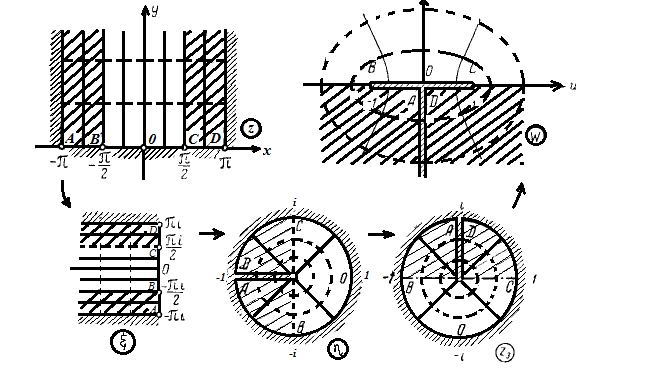
Рисунок 3.2.2.
Видно, что
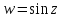 в комплексной плоскости не ограничен.
Например, в лучах
в комплексной плоскости не ограничен.
Например, в лучах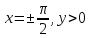 ,
он принимает действительные значения,
по модулю большие единицы.
,
он принимает действительные значения,
по модулю большие единицы.
Отметим, что в (замкнутой) полосе
 функция
функция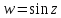 принимает значение 0 лишь в точках
принимает значение 0 лишь в точках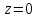 и
и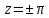 .
Учитывая нечетность и периодичность
этой функции, отсюда можно заключить,
что она обращается в 0 лишь на действительной
оси в точках
.
Учитывая нечетность и периодичность
этой функции, отсюда можно заключить,
что она обращается в 0 лишь на действительной
оси в точках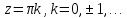
Заметим, что отображение
 в силу соотношения
в силу соотношения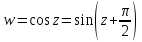 можно представлять, как только что
рассмотренное, лишь со сдвигом.
можно представлять, как только что
рассмотренное, лишь со сдвигом.
6. Гиперболические функции и
С тригонометрическими функциями тесно связаны гиперболические функции, определяемы посредством формул
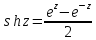 ,
,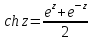 .
(3.3.1)
.
(3.3.1)
Эти функции всюду аналитичны. Они просто выражаются через тригонометрические функции:
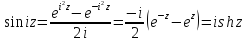
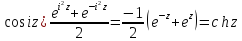 ,
,
то есть
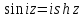 ,
,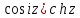 ,
и поэтому несущественно отличаются от
них.
,
и поэтому несущественно отличаются от
них.
