3. Функция Жуковского

Функция

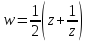(2.3.1)

называется функцией Жуковского.

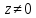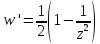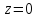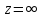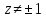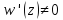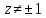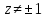Эта функция была введена в рассмотрение русским ученым Н.Е. Жуковским в теории крыла самолета и имела важные приложения, поэтому носит его имя.Эта функция регулярна в точках , ∞, причемв точкахиимеет полюсы первого порядка. Следовательно, функция Жуковского (1) однолистна в каждой точке, так какпри, и неоднолистна в точках,, так как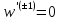

Рассмотрим основные свойства функции Жуковского.

1. Однолистность.

Функция Жуковского 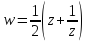однолистна в области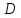тогда и только тогда, когда в этой области нет различных точек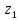и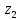, связанных равенством

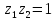(2.3.2)

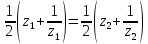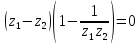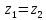В самом деле, пусть . Тогда, откуда либо, либо.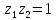

Равенство (2.3.2) геометрически означает, что точка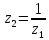, получается из точки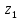двойной симметрией: относительно окружности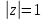и относительно прямой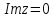(Рис. 2.3.1).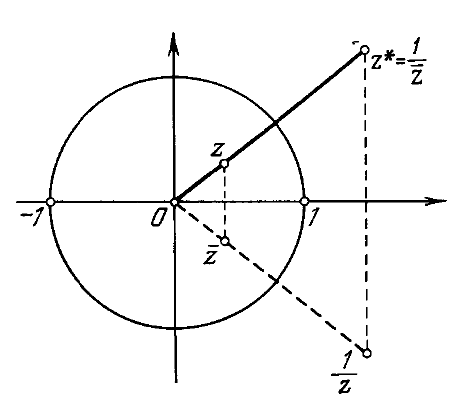

Рисунок 2.3.1.

Таким образом, функция Жуковского однолистна в области в том и только в том случае, когда эта область не содержит ни одной пары различных точек, которые получаются одна из другой двойной симметрией: относительно единичной окружности и относительно действительной оси.

Функция Жуковского 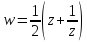однолистна в следующих областях:

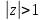• — внешность единичного круга,

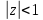• — внутренность единичного круга,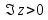

• — верхняя полуплоскость

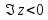• — нижняя полуплоскость

2. Образы окружностей и лучей.

Найдем образы окружностей 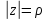и лучей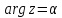(полярная координатная сетка) при отображении функцией Жуковского. Полагая в (3.3.1)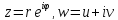, получаемы, откуда применив формулы Эйлера получим:

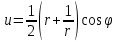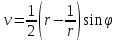, (2.3.3)

Рассмотрим окружность

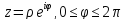(2.3.4)

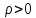(— фиксировано). Из (3.3.3) следует, что при отображении функцией Жуковского образом окружности (3.3.4) является эллипс

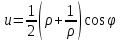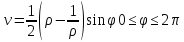, (2.3.5)

с полуосями 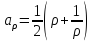,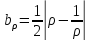и с фокусами в точках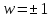(так как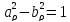). Исключаяиз уравнений (3.3.5) параметр, при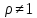уравнение этого эллипса можно записать в каноническом виде:

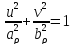(2.3.6)

Отметим, что при замене 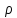на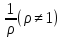эллипс (2.3.5) остается тем же самым, но его ориентация меняется на противоположную. На рис. 2.3.2 показаны окружности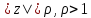, ориентированные по часовой стрелке, и их образы — эллипсы (2.3.6)

Рисунок 2.3.2.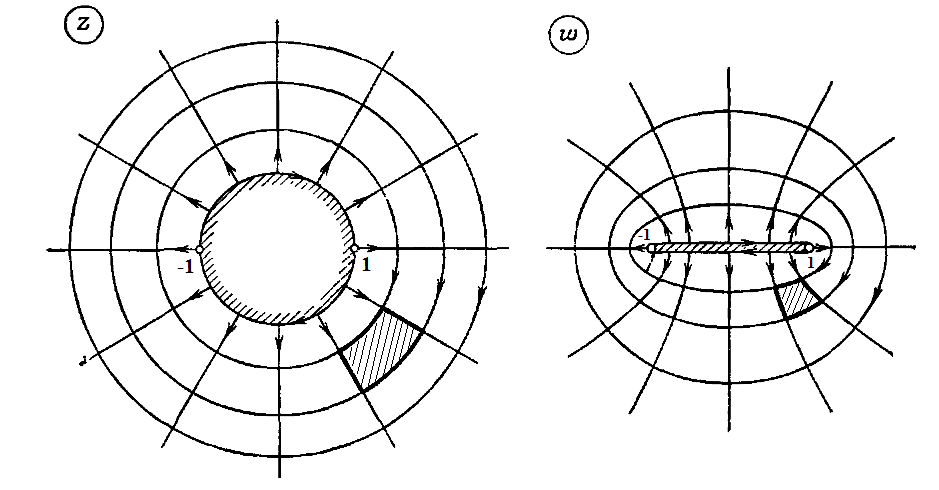

Из (2.3.5) видно, что эти эллипсы ориентированы также по часовой стрелке. На рис. 2.3.3 показаны окружност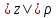и при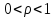и их образы — эллипсы (2.3.6); при этом ориентация меняется на противоположную: окружность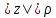, ориентированная против часовой стрелки, переходит в эллипс (2.3.6), ориентированный по часовой стрелке.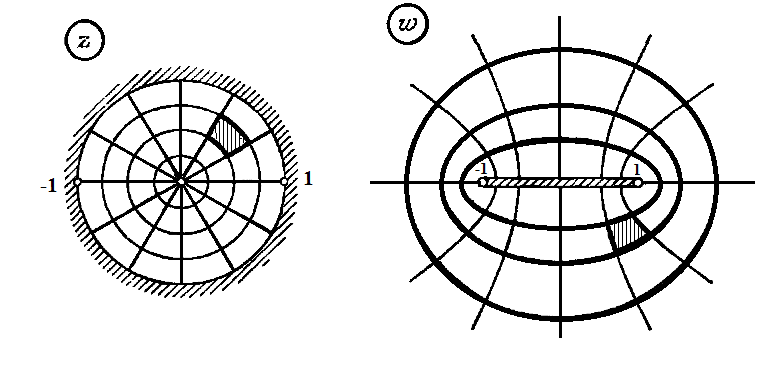

Рисунок 2.3.3.

При 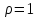эллипс (3.3.5) вырождается в отрезок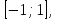проходимый дважды, т. е. окружность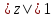переходит в отрезок [—1, 1], проходимый дважды (рис. 3.3.2, 3.3.3).

Рассмотрим луч

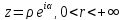(2.3.7)

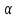(— фиксировано). При отображении функцией Жуковского образом этого луча (см. (3.3.3)) является кривая

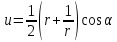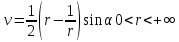, (2.3.8)

Исключаяиз уравнений (3.3.8) параметр 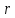, при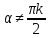(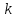— целое), получаем

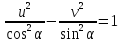(2.3.9)

Кривая (2.3.9) — гипербола с фокусами в точках 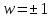и с асимптотами.

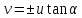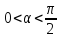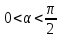Если , то кривая (2.3.8) является правой ветвью гиперболы (2.3.9), т. е. луч (2.3.7) припереходит в правую ветвь гиперболы (2.3.9) (ориентация показана на рис. 2.3.4).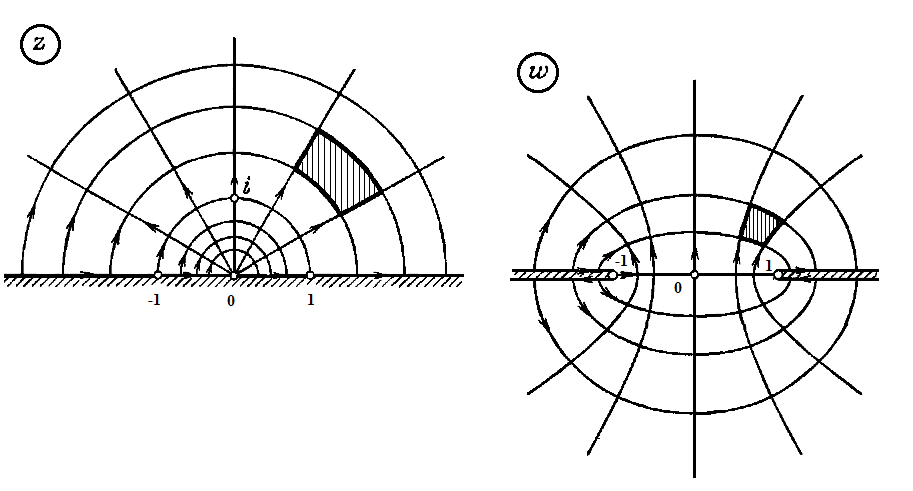

Рисунок 2.3.4.

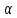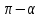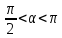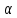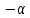При замене в (2.3.8) наполучается левая ветвь той же гиперболы (2.3.9), поэтому луч (2.3.7) припереходит в левую ветвь гиперболы (2.3.9) (рис. 2.3.4). Отметим также, что при замене в (2.3.8)наполучается та же ветвь гиперболы (2.3.9), но ее ориентация меняется на противоположную.

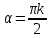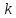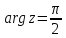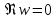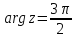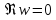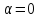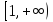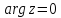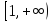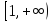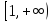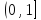Рассмотрим лучи (2.3.7) при (— целое). Из (2.3.8) следует, что лучпереходит в мнимую ось(рис. 2.3.4). Лучтакже переходит в мнимую ось. Прикривая (2.3.8) вырождается в лучпроходимый дважды (сложенный вдвое) (рис. 2.3.4), т. е. лучпереходит в луч, проходимый дважды: лучпереходит в лучи полуинтервал– в луч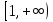(рис. 2.3.4). Аналогично, луч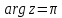переходит в луч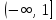, проходимый дважды (рис. 2.3.4).

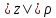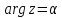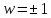Таким образом, функция Жуковского переводит окружностив эллипсы (2.3.6), а лучи– в ветви гипербол (2.3.9); фокусы всех эллипсов (2.3.6) и гипербол (2.3.9) расположены в точках; любой эллипс (2.3.6) пересекается с любой гиперболой (2.3.9) под прямым углом.