Элементы аналитической геометрии

§1. Метод координат на плоскости

1. Декартовы прямоугольные координаты

Выберем на плоскости две взаимно перпендикулярные прямые: Ох и Оу с указанными на них положительными направлениями.

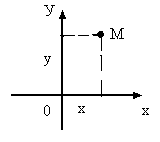
Ох, Оу – координатные оси.

О – начало координат

За положительное направление на оси Ох примем направление слева направо, а за положительное направление на Оу - сверху вниз.

Возьмем некоторую единицу масштаба, с помощью которой будут производиться все измерения на плоскости ХОУ.

Совокупность координатных осей Ох, Оу и выбранная единица масштаба называется декартовой прямоугольной системой координат на плоскости.

Произвольной точке М на плоскости поставим в соответствии два числа: абсциссу х, равную расстоянию от точки М до оси Оу, взятому со знаком «+», если точка М лежит правее оси Оу и со знаком «-», если точка М лежит левее оси Оу; ординату у равную расстоянию от точки М до оси Ох, взятому со знаком «+» , если М лежит выше Ох и со знаком «-», если М лежит ниже Ох.

Абсцисса х и ордината у называются декартовыми прямоугольными координатами точки М и обозначаются М (х; у).

Отметим, что каждой точке плоскости соответствует пара действительных чисел х и у. Верно и обратное, каждой паре действительных чисел х и у соответствует 1 точка плоскости. Это значит, что на плоскости положение произвольной точки М полностью определяется ее координатами х и у.

Координатные оси Ох и Оу разбивают плоскость на I-ый - IV-ый координатные углы.

	I	II	III	IV
х	+			+
у	+	+		

2. Полярные координаты

Зафиксируем на плоскости точку О и выходящую из нее полупрямую Ор, а также выберем единицу масштаба.

О– полюс

Ор – полярная ось

Произвольной точке М плоскости поставим в соответствие 2 числа: полярный радиус (г), равный расстоянию от точки М до полюса О, измеренному в выбранной единице масштаба.

Полярный угол  (фи),  измеряется в радианах:    

Полюсу О соответствует полярный г=0; полярный угол для него не определен.

3. Связь между прямоугольной декартовой системой координат и полярной системой координат.

П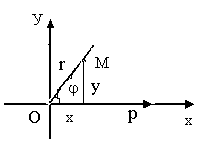усть точка М задана в полярной системе координат, т.е. она характеризуется полярным радиусом г и полярным углом. Найдем прямоугольные декартовые координаты данной точки.

 OLM – прямоугольный

cos  = ;sin  =

(1)

Пусть точка М задана своими прямоугольными декартовыми координатами. Найдем полярные координаты данной точки

Дано х и у. Найти r и 

Из треугольника  OLM:

(2);

=arctg;

Формулы (1) и (2) верны при любом расположении точки М.

Пример 1.

Дана точка А с координатами: х = 1, у = 1. Найдем полярные координаты точки А.

r==,tg==1 =arctg1 =.

Пример 2.

Даны полярные координаты точки А: r=2, =. Найдем ее прямоугольные координаты.

Пользуясь формулами (1), находим х=r·cos=r·cos=0,у=r·sin=r·sin=2.

4. Основные задачи, решаемые методом координат

I. Задача о расстоянии между двумя точками.

Даны точка М₁ (х₁, у₁) и точка М₂ (х₂, у₂). Найти расстояние М₁М₂=d.

M₁NM₂ – прямоугольный.

По теореме Пифагора: d =

M₁N = x₂ – x₁ (расстояние между двумя точками на числовой оси)

NM₂ = y₂ – y₁

(3) d =

Пример 3.

Дана точка А(-1;-2), В(-4;2), d=АВ-?

Решение.

По формуле (3): d===5.

II. Задача о делении отрезка в данном отношении.

Дано:

М₁ (х₁; у₁), М₂ (х₂; у₂), = . М (х; у) -?

По теореме Фалеса о пересечении сторон угла параллельными прямыми будет выполняться соотношение:

=

M₁N=x₂–x₁, NM₂=y₂–y₁, =,

 (x₂–x)=х-x₁,  x₂-х=х-x₁, х+х=x₂+x₁,

(4) х=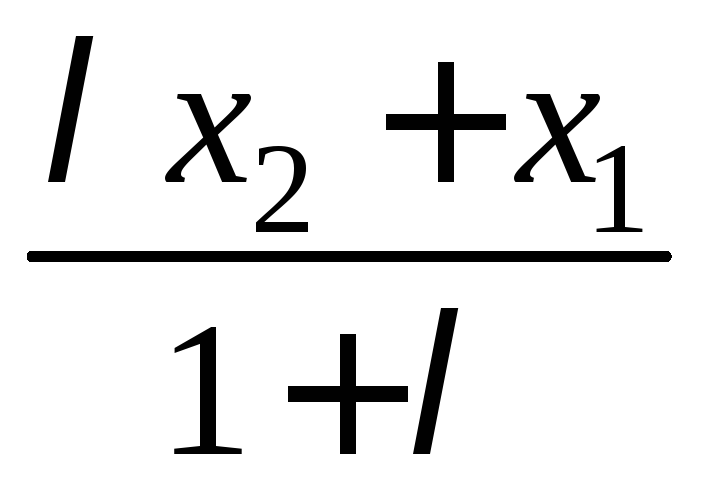; у=.

Пример 4.

М₁(1;1), М₂ (4;7), =2. М (х; у) -?

Решение.

Применим формулы (4). λ=2, х==3; у==5М (3; 5).

Решение задач

Задача 1. Определить координаты вершин равностороннего треугольника, лежащего в I-ом квадрате со стороной 10, если один из его вершин совпадает с началом координат (т.О), а основание треугольника расположено на оси Ох.

Решение.

По условию О (0; 0), С (10; 0). Так как треугольник равносторонний, то В (5; y).

Найдем расстояние ОВ по формуле (3).

10 = , 100=25+y², у² =75, у =

В = (5; ).

Задача 2. Найти координаты вершин квадрата, если его диагональ d = 5 ед. длины.

Решение.

О (0;0) – точка пересечения диагоналей,

Диагонали - на осях координат

А (0; -2,5), С (0; 2,5), В (2,5; 0), D (-2,5; 0)

Задача 3. На оси абсцисс найти точку, находящуюся на расстоянии d = 10 от точки А (2; 6).

Решение.

Так как точка М лежит на оси Ох, то ее координаты М(х; 0). Применим формулу (3):10=, (2-х)²+36=100, (2-х)² =64, 2–х=8,

2-х=8x=-6, 2-х=-8x=10.

Или: х²–4х+4=64, х²–4х-60=0,

D=16-4·1·(-60)=16+240=256

x_1,2=,x₁=10, x₂=-6.

M₁ (10; 0) и M₂ (-6; 0)

Задача 4. Найти точку М(х;у), равноудаленную от точек О(0;0), А(-4;0) и В(0;8)

Решение.

ОМ=МА=МВ  ОМ²=МА²=МВ²

ОМ²=х²+у² , МВ²=х²+(у-8)², МА²=(х+4)²+у²

х² +у² =х²+(у-8)², х²+у² =(х+4)²+у²,

у² =у²-16у+64, х²=х²+8х+16,-

16y=64, -8х = 16,

у=4, х = -2,

М (-2; 4)

Задача 5. Вычислить площадь равностороннего треугольника, если заданы две его вершины: А (-3; 2) и С (1; 6).

Решение.

S_=, а=АС, АС=

S_=.

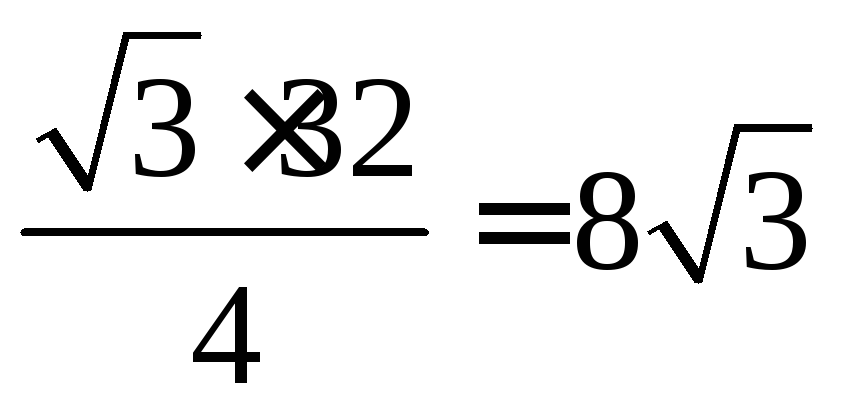Задача 6. Построить точки по их полярным координатам: А(5;0), В(2;), С(3;), D(1;).

Решение.

Задача 7. Найти полярные координаты точек А (1; 1), В (0; 2), С (-3; 3).

Решение.

А:r=;=arctg1=, А,

B: r=2;  =arctg0=,В,

C: r==; =arctg(-1)=,С.

Задача 8. Какие прямоугольные координаты имеют точки, заданные полярными координатами А(5; 0), В, С?

Решение.

А: х=r·cos=5·1 =5; у=r·sin=5·0=0; А(5;0),

В: х=6·cos45^о =6·=3; у=6·=3;

В(3;3)

С: х=2·0=0; у=2·1=2, С(0;2).