§ 11. Обобщение действий сложения и умножения

Приведем индуктивные определения для суммы и произведения конечного числа натуральных чисел.

Определение 1. Суммой n натуральных чисел (n—натуральное число) х₁, х₂, …, х_n, называется натуральное число, обозначаемое символом

= х₁ + х₂ + … + х_n

и определяемое условиями:;

Определение 2. Произведением n натуральных чисел (n — натуральное число) х₁, х₂, …, х_n, называется натуральное число, обозначаемое символом

= х₁ х₂… х_n

и определяемое условиями: (3) =х₁, (4) =.

Применяя обобщенный принцип полной математической индукции, можно доказать справедливость законов: коммутативного и ассоциативного для сложения и умножения и дистрибутивного закона, связывающего сложение с умножением. Докажем, например, обобщенный закон дистрибутивности на случай п слагаемых:

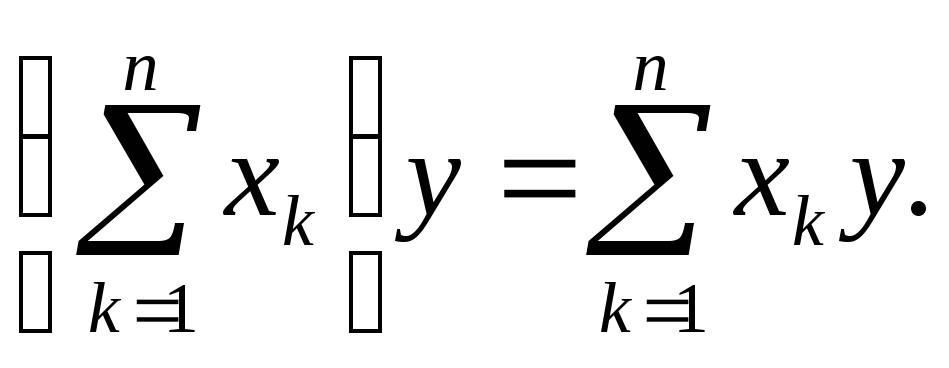(5)

Применим обобщенный принцип индукции:

При n=2, имеем: 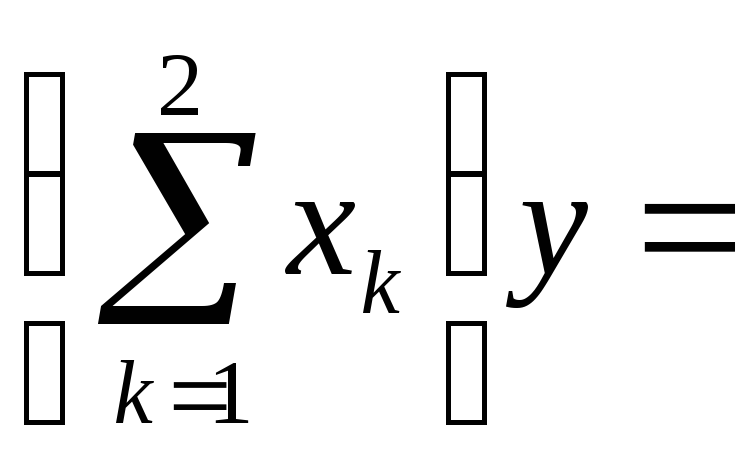(х₁ + х₂)у = х₁у +х₂у =

Это равенство верно в силу дистрибутивного закона для суммы двух чисел.

Допустим, что формула (5) верна для п:

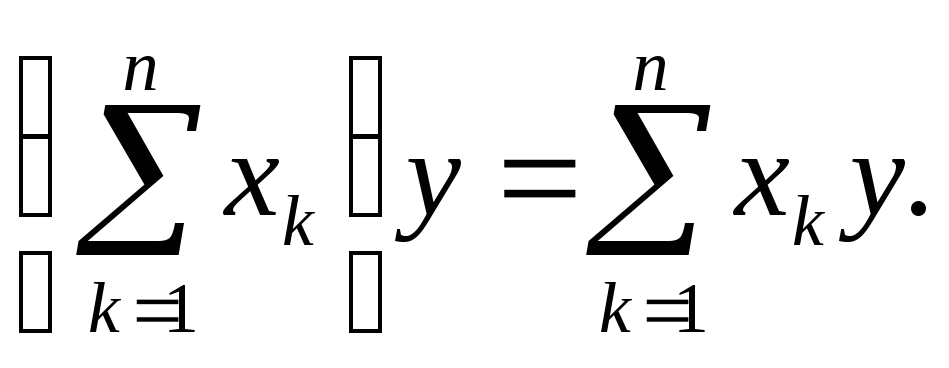
Докажем, что она будет верна для n' = n + 1:

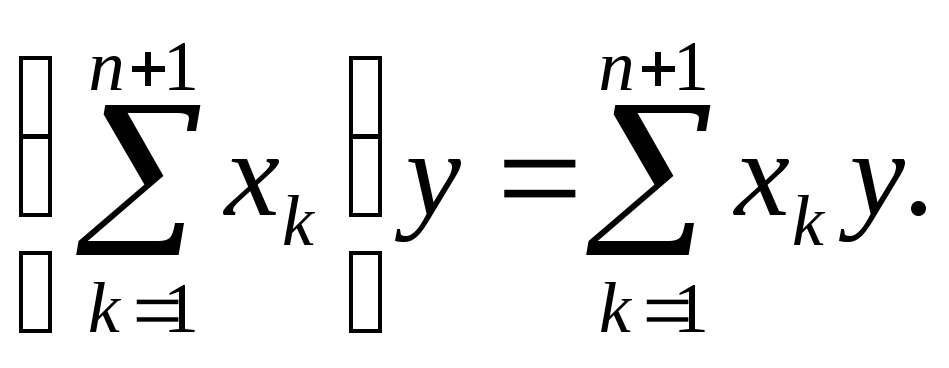
Действительно, 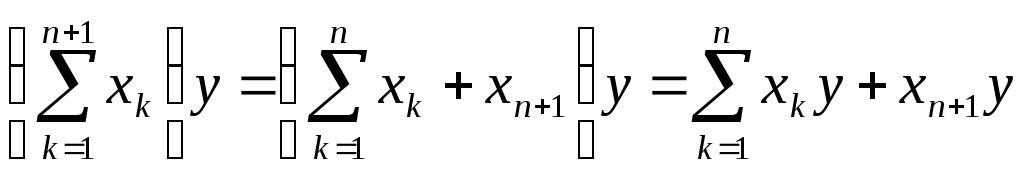, следовательно,

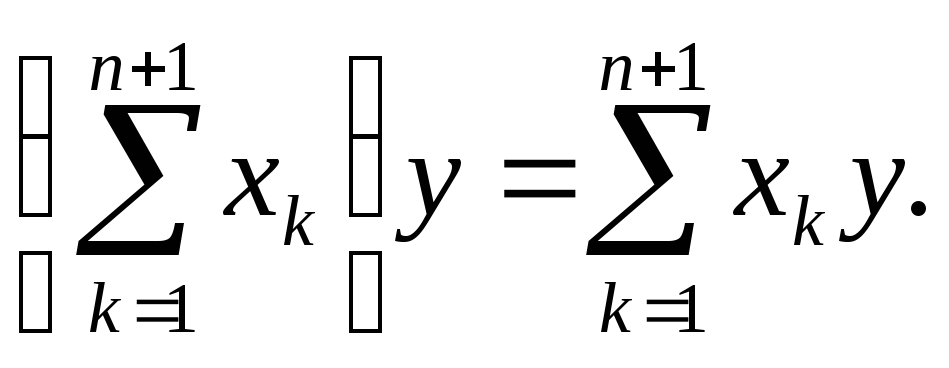
Дистрибутивный закон доказан. Он верен и в том случае, когда ,

т. е. .

Для доказательства сначала рассматривается у как один член, затем заменяют его через сумму.

§ 12. Принципы расширения при построении числовых систем. Разбиение множества nn на классы эквивалентности. Множества целых чисел

При построении числовых систем Z, Q, R, C, H используют принципы расширения.

Принципы расширения

Пусть построена некоторая система F₁ и требуется построить некоторую систему F₂, которое должно удовлетворять следующим принципам:

1) .

2) В F₂ должны выполняться все операции, которые выполнимы в F₁ , причем их смысл должен быть один и тот же, то есть результат выполнения операций в F₁ и F₂ должен быть одинаков, если на него смотреть как на элемент из F₂ .

3) В F₂ должна быть некоторая операция, которая в F₁ либо не выполняется, либо выполняется частично.

4) F₂ должно быть минимальной системой, удовлетворяющей 1-3.

Будем считать, что система натуральных чисел в N уже построена.

Определение 1. Кольцом целых чисел называется минимальное кольцо, содержащее N в качестве своего подполукольца.

Определение 1 согласуется с принципами расширения 1-4. Действительно, при F₁=N и при F₂= Z получаем:

1) 

2) В  выполняется операции “+” “” , причем их смысл одинаков.

3) В  выполняется операция вычитания, то есть сложение с противоположным элементом, а в N эта операция выполняется частично.

4) - минимальная система, удовлетворяющая 1-3.

Для того, чтобы доказать, что множество целых чисел существует, его нужно построить, то есть построить его модель.

Рассмотрим множество NN. Оно состоит

На множестве введем отношение.

Определение 2. Упорядоченные пары (a,b) и (c,d) из называютсяравносильными и обозначают (a,b) ~ (c,d), если a+d=b+c.

Таким образом

Лемма 1. Отношение ~ на множестве является отношением эквивалентности.

Доказательство.

1. Рефлексивность.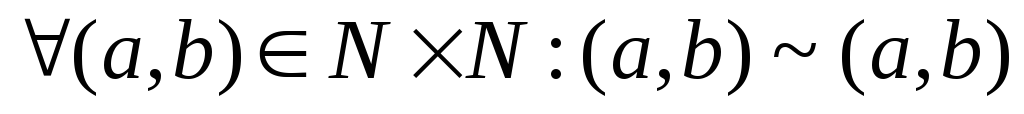, так какa+b=b+a.

2. Симметричность.

Пусть

3. Транзитивность.

ПустьПокажем, что

Из 1 следует, что a+d=b+c

Из 2 следует, что c+n=d+m

Из 1-3 следует, что отношение ~ является отношением эквивалентности.

По основной теореме об отношении эквивалентности множество разбивается отношением ~на непересекающиеся классы.

Определение 3. Множество ( по отношению ~) всех классов эквивалентности, на которые разбивается множествоотношением ~, обозначается и называется множеством целых чисел, а его элементы называются целыми числами.