§ 2. Аксиомы натуральных чисел (аксиомы Пеано) и простейшие следствия из них

Аксиоматическое построение данной теории начинается с перечисления основных отношений (принимаемых, без определения) и основных свойств или аксиом (принимаемых без доказательства), которым удовлетворяют данные отношения. При аксиоматическом построении натуральных чисел вводится одно основное отношение и четыре аксиомы.

Определение 1. Натуральным рядом называется непустое множество N, элементы которого называются натуральными числами, в котором задано унарное отношение ' (штрих),которое записывается в виде a'=b, читается: «b следует за a» или «b есть число, следующее за числом a», удовлетворяющее следующим аксиомам:

1. Существует элемент 1, не следующий ни за каким числом, т. е. a' 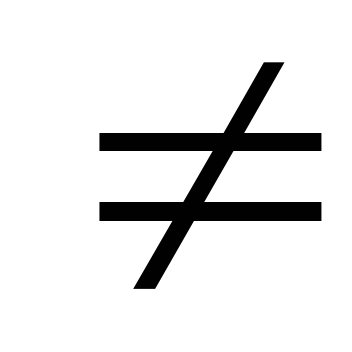1 для любого числа аN.

2. Для любого числа a существует следующее за ним число a' и притом только одно, т. е. из a=b следует a'=b',

3. Любое число следует не более чем за одним числом, т. е. из а' =b' следует a = b.

4. (Аксиома индукции.) Любое подмножество М множества N натуральных чисел, обладающее свойствами:

А) 1 принадлежит М,

Б) если число a принадлежит М, то следующее число a' также принадлежит М,

содержит все натуральные числа, т. е. совпадает с N.

Приведенная здесь аксиоматика натуральных чисел представ­ляет собой лишь несущественное изменение системы аксиом, предложенной в конце прошлого века итальянским математиком и логиком Пеано.

Замечание. Аксиомами Пеано I-IV, определяется множество натуральных чисел, понятие же натурального числа относится к неопределяемым понятиям.

Определение 2. Если b следует за а, то говорят, что а есть число, предшествующее числу b, или что а предшествует b.

Согласно аксиоме I число 1 не имеет предшествующего. Но это единственное число с таким свойством.

Теорема 2. Любое, число имеет предшествующее число и притом только одно.

Доказательство. Пусть М — множество, содержащее 1 и все числа, имеющие хотя бы одно предшествующее число.

А) 1 принадлежит М, Б) если а принадлежит М, то и а' также принадлежит М, ибо а' имеет предшествующее число а (пред­положение, что а принадлежит М, здесь даже излишне). По аксиоме IV множество М содержит все числа. Значит, любое число имеет по крайней мере одно предшествующее.Единственность предшествующего числа следует из аксиомы III, согласно которой любое число имеет не более одного предше­ствующего.

Теорема 3. Если числа, следующие за данными числами, различны, то и данные числа различны, т. е. из а'b' следует .

Доказательство. По аксиоме II из а = b следует а'= b'.

Теорема 4. Если данные числа различны, то и следующие за ними различны, т. е. из а b следует а'b'.

Доказательство. По аксиоме III из а'= b' следует а = b.

Теорема 5. Любое число отлично от следующего за ним числа, т. е. аа'для любого а.

Доказательство. Пусть М - множество чисел, для которых теорема верна, т. е. множество таких чисел, которые не совпадают со следующим за ними числами.

А) По аксиоме I: а'1 для любого числа а, в том числе а1, т. е. 1'1, а, значит, 1 принадлежит М.

Б) Если а принадлежит М, то а'а. Значит, по теореме 4 также (а')'а', т.е. а' принадлежит М. По аксиоме IV М содержит все числа, т. е. аа'для любого а.