§27. Множество комплексных чисел

Определение 1. Полем комплексных чисел C называется минимальное расширение поля R, содержащее один корень уравнения х²+1=1.

Определение 1 согласуется с принципами расширения 1-4. Действительно, при F₁=R и при F₂= C получаем:

1) RC

2) В C выполняются операции “+” “·”, “–” и “:” причем их смысл одинаков.

3) В С разрешимы уравнения 2-й степени, в R разрешимы только те из этих уравнений, дискриминант которых больше либо равен нулю.

4) С- минимальная система, удовлетворяющая 1-3.

Для того, чтобы доказать, что множество комплексных чисел существует, его нужно построить, то есть построить его модель.

Рассмотрим множество RR. Оно состоит

Определение 2. Суммой комплексных чисел (a,b) и (c,d) называется комплексное число. (a,b) + (c,d) =(a+с,b+d).

Теорема 1. Алгебраическая система < C, + > является абелевой группой.

Доказательство. Из определения следует, что операция + является алгебраической на C.

1) Т.к. сложение пар покоординатно, то сложение пар обладает теми же свойствами, что и сложение действительных чисел, а значит БАО «+» ассоциативно и коммутативно на C.

2) (0,0) C является нулевым элементом в C.

3).

Итак, <C,+> - абелева группа.Теорема доказана.

Определение 1. Произведением комплексных чисел (a,b) и (c,d) называется комплексное число (a,b) · (c,d) = (ac-bd, ad+bc).

Теорема 2. Алгебраическая система < C^♯, · > является абелевой группой.

Доказательство. Из определения следует, что операция · является алгебраической на C^♯.

1) Покажем, что операция · является ассоциативной на C^♯. Пусть (a,b), (c,d) и (k,l) C^♯.

((a,b)·(c,d)) · (k,l)=(ac-bd,ad+bc)·(k,l)=((ac-bd)k-(ad+bc)l,(ac-bd)l+(ad+bc)k)

(a,b)·((c,d) · (k,l))= (a,b)·(ck-dl,cl+dk)=(a(ck-dl)-b(cl+dk),a(cl+dk)+b(ck-dl))

Левые части равны, значит правые части равны => БАО «» ассоциативно.

II.2. Покажем, что элемент (1,0) C является единичным в C.

Действительно,

(a,b)·(1,0)= (a·1-b·0,a·0+b·1)=(a,b), аналогично,

(1,0) ·(a,b)= (a,b).

II.3. Пусть (a,b)C^# (т.е. (a,b)). Покажем, что

(ax-by, bx+ay)=(1,0)

Итак,

(Этот элемент будет и левым обратным, а значит и просто обратным).

II.4. Коммутативность умножения показывается аналогично ассоциативности. Теорема доказана.

Теорема 2. Алгебраическая система < ℚ^♯,+, · > является полем.

Доказательство.

3. По теореме 1' < C, + > - абелева группа.

4. По теореме 2' < C^♯, · > - абелева группа.

3) Проверим, что в C выполняются дистрибутивные законы. Пусть (a,b), (c,d) и (k,l) C

((a,b)+(c,d)) (k,l)=(a+c,b+d)(k,l)=((a+c)k-(b+d)l,(a+c)l+(b+d)k)=

=(ak+ck-bl-dl,al+cl+bk+dk)=(ak-bl,al+bk)+(ck-dl,cl+dk)=(a,b)(k,l)+(c,d)(k,l).

Таким образом, в C выполняется правый дистрибутивный закон. Поскольку операция · является коммутативной на C, то в C выполняется и левый дистрибутивный закон.

Из 1)-3) следует, что < C^♯,+, · > - поле. Теорема доказана.

Чтобы показать, что C является полем комплексных чисел, необходимо:

1. поле R вложить в качестве подполя в C;

2. показать, что C содержит корень уравнения x²+1=0

Рассмотрим в C подмножество R₁={(a,0):aR}

Зададим отображение φ: R→R₁ по правилу: φ(a)=(a,0) Покажем, что φ - гомоморфизм полей:

^φ(b) и

Покажем, что - биекция:

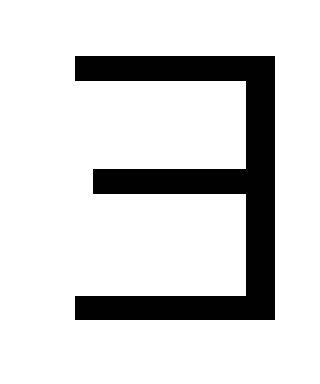1. Т.к. (k,0) R₁ kR: φ(k)=(k,0), то φ – сюръекция.

2. Пусть φ(a)= φ(b) для некоторых a и b. Тогда, (a,0)=(b,0) a=b => φ – инъекция.

Итак, φ - изоморфизм. RR₁, R₁ – поле.

Т.к. изоморфные поля обладают одинаковыми свойствами, и с точки зрения алгебры неразличимы, то R₁ можно отождествлять с R, и, значит, можно считать, что К является подполем C, отождествляя (a,0)a, .

Покажем, что (0,1)является корнем уравненияx²+1=0. Обозначим i=(0,1) и назовем его мнимой единицей, тогда,

i²=(0,1)(0,1)=(00-11, 01+10)=(-1,0)-1 =>i – корень уравнения (1). Следовательно, C удовлетворяет определению поля комплексных чисел.