§20.. Фундаментальные последовательности рациональных чисел.

Определение 3. Последовательность рациональных чисел называется фундаментальной, если

Условимся для краткости, вместо фразы «фундаментальная последовательность рациональных чисел», писать ФП. Самым простым примером ФП является стационарная последовательность . Всякая БМ также является фундаментальной.

В самом деле, пусть - БМ иr >0. Тогда

Далее имеем:

и фундаментальность последовательности доказана.

Отметим некоторые свойства фундаментальных последовательностей.

Теорема 1. Всякая ФП является ограниченной последовательностью.

Доказательство. Пусть - ФП. Тогда. Так как, то получаем.

По лемме 1, в конечном множестве есть наибольший элемент, обозначим его М. Тогда имеем, а это означает ограниченность последовательности.

Теорема 2. Сумма двух ФП есть ФП.

Доказательство. Пусть - ФП,- ФП и. Покажем, что- ФП. Зададимся числомr > 0. Из фундаментальности последовательностей иполучаем соответственно:

Положим , тогда для любогоp будем иметь:

. Таким образом - ФП

Теорема 3. Произведение двух ФП есть ФП.

Доказательство. Пусть - ФП,- ФП и. Покажем, что- ФП. Заметим, прежде всего, что из фундаментальности последовательностейиследует по теореме 1 их ограниченность. Значит,

, .

Зададимся числом r >0. Из фундаментальности последовательностей иполучаем, соответственно:

Если положить , то приполучим:

Итак, , а это означает, что- ФП.

Следствие 1. Если - ФП, ас - рациональное число, то - Фп.

Следствие 2. Если - ФП, то- ФП.

Следствие 3. Разность двух ФП есть ФП.

Нам осталось рассмотреть вопрос о делении фундаментальных последовательностей. Предварительно сформулируем и докажем важную лемму.

Лемма 3. Пусть - ФП не являющаяся бесконечно малой. Тогда существуют рациональное числоd>0 и натуральное число N, такие, что последовательность удовлетворяет одному из двух условий:

1.

2.

Доказательство. Так как , по условию, последовательность не является БМ, то . Иными словами, бесконечное множество членов последовательностиудовлетворяет неравенству(1).

Докажем, что, с другой стороны, неравенству удовлетворяет лишь конечное множество членов последовательности.

Предположим противное, что неравенству (2) удовлетворяет бесконечное множество членов последовательности. Из фундаментальности последовательностиполучаем:

(3).

Так как, кроме того , то(4).

Мы предположили, что неравенству (2) удовлетворяет бесконечное множество членов последовательности . Поэтому найдется номертакой, что(5).

Из неравенства (4) следует, что , а из неравенства (5) получаем, что. Но это означает, что неравенству (1) может удовлетворять лишь конечное множество членов последовательности(лишь члены с номерами, не превосходящими), а это противоречит сказанному выше о неравенстве (1).

Итак, неравенству (2) удовлетворяет лишь конечное множество членов последовательности . Пусть- наибольший из номеров членов последовательности, которые удовлетворяют неравенству (2). Тогда дляn> и тем более (6).

Покажем, что, начиная с номера , все члены последовательностилибо положительны, либо отрицательны. Предположим, что это не так, то есть, что существуютn≥N и m≥N такие, что иимеют разные знаки, например,>0,<0. Так как, то из неравенства (3) получаем, то есть(7).

С другой стороны, так как , то из неравенства (6) получаеми, то есть, а. В таком случае, а это противоречит неравенству (7).

Итак, начиная с номера N, все члены последовательности либо положительны, либо отрицательны, значит либо, либо. Лемма доказана.

В дальнейшем нам часто придется иметь дело с фундаментальными последовательностями рациональных чисел, не являющимися бесконечно малыми и не содержащими членов, равных 0. такие последовательности условимся называть регулярными.

Лемма 4. Если - регулярная последовательность, то существует такое положительное рациональное числоe, что .

Доказательство. регулярная последовательность удовлетворяет условиям леммы 3, поэтому.

Положив , получаемдля любогоn, что и требовалось доказать.

Теорема 4. Если - регулярная последовательность, то- ФП.

Доказательство. По лемме 4 . Зададимся рациональным числомr>0. Из фундаментальности последовательности получаем:

.

Тогда при n≥N и всех p 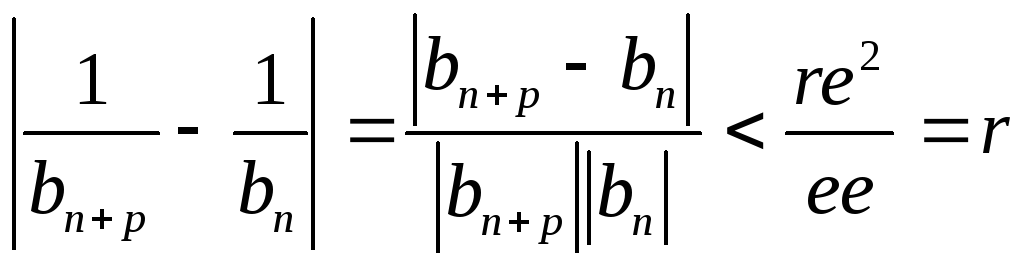, а это означает фундаментальность последовательности.

Следствие. Если - ФП, а- регулярная последовательность, то- ФП.

Это без труда получается из теорем 3и 4.