
- •1.Основные физические законы электромеханического преобразователя энергии.
- •1.1 Закон электромагнитной индукции.
- •1.2 Закон электромагнитного взаимодействия.
- •1.3 Законы электромеханики.
- •1.4 Сердечники магнитопроводов электрических машин.
- •1.5 Обмотки электрических машин.
- •1.6 Потери энергии и коэффициент полезного действия
- •1.7 Нагревание и охлаждение электрических машин
- •2. Трансформаторы
- •2.1 Назначение и общие сведения о трансформаторах.
- •2.2 Основы теории однофазного трансформатора. Режим холостого хода.
- •2.3 Векторная диаграмма трансформатора в режиме холостого хода.
- •2.4 Уравнения, схема замещения нагруженного однофазного трансформатора. (Рабочий режим).
- •2.5 Изображение векторной диаграммы приведенного трансформатора.
- •2.6 Опытное определение параметров схемы замечания трансформаторов. Опыты холостого хода и короткого замыкания.
- •2.7 Вторичное напряжение трансформатора. Внешняя характеристика.
- •2.8 Мощность потерь и к.П.Д. Трансформатора.
- •2.9 Магнитные системы трехфазных трансформаторов.
- •2.10 Схемы и группы соединений трёхфазных трансформаторов.
- •2.11 Параллельная работа трансформаторов.
- •2.12 Автотрансформаторы.
- •Специальные трансформаторы
- •2.13.1 Трансформаторы частоты.
- •2.13.2 Трансформатор числа фаз.
- •2.13.3 Трансформаторы для электрических печей.
- •2.13.4 Сварочные трансформаторы.
- •2.13.6 Трансформаторы звуковой и ультразвуковой частот. Реакторы.
- •2.13.7 Измерительные трансформаторы.
- •2.13.8 Трансформаторы тока.
- •2.13.9 Трансформаторы напряжения.
- •Асинхронные электрические машины.
- •3.1 Области применения. Конструкция асинхронных машин.
- •3.2 Обмотки асинхронных машин.
- •3.3 Энергетические диаграммы асинхронных машин.
- •3.4 Схема замещения трехфазной асинхронной машины.
- •3.5 Опытное определение параметров схемы замещения асинхронной машины.
- •3.6 Электромагнитный момент асинхронной машины.
- •3.7 Механические характеристики электрических машин и производственных механизмов
- •3.8 Совместная механическая характеристика электрического двигателя и производственного механизма.
- •3.9 Пуск асинхронных двигателей.
- •3.10 Регулирование частоты вращения асинхронных двигателей.
- •3.11 Однофазные двигатели
- •3.12 Асинхронные машины автоматических устройств.
- •3.13 Специальные асинхронные машины.
2.3 Векторная диаграмма трансформатора в режиме холостого хода.
Векторная диаграмма трансформатора, находящегося в режиме холостого хода будет тоже аналогична векторной диаграмме индуктивной катушки с ферромагнитным сердечником (Рис. 2.2).
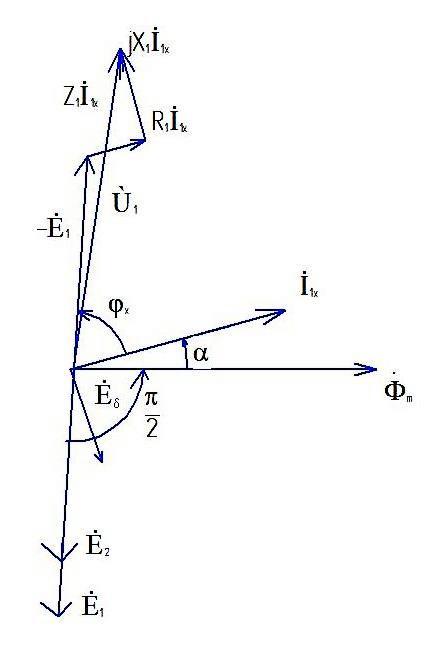
Рисунок 2.2 Векторная диаграмма трансформатора в режиме холостого хода
Из
векторной диаграммы трансформатора
находящегося в режиме холостого хода
(Х.Х.) видно, что сдвиг фаз между ![]() близок к
близок к ![]() вследствие чего коэффициент мощности
вследствие чего коэффициент мощности
![]() - угол потерь.
- угол потерь.
Мощность потребления электрической энергии трансформатора в режиме Х.Х. при номинальным первичном напряжении соответствует номинальным потерям энергии в магнитопроводе трансформатора, которые связаны с его перемагничиванием и вихревыми токами в нем. Эта мощность невелика и составляет до 1,5% номинальной мощности трансформатора.
2.4 Уравнения, схема замещения нагруженного однофазного трансформатора. (Рабочий режим).
Включение
нагрузки ![]() сопровождается появлением тока
сопровождается появлением тока ![]() во вторичной обмотке трансформатора
(Рис. 2.3).
во вторичной обмотке трансформатора
(Рис. 2.3).

Рисунок 2.3 Картина магнитного поля нагруженного однофазного трансформатора.
Ток
![]() создает м.д.с.
создает м.д.с. ![]() которая в соответствии с законом Ленца
противодействует м.д.с. первичной обмотки
которая в соответствии с законом Ленца
противодействует м.д.с. первичной обмотки
![]() .
При этом возникает переменный магнитный
поток рассеяния вторичной обмотки
.
При этом возникает переменный магнитный
поток рассеяния вторичной обмотки ![]() уменьшается входное сопротивление
трансформатора, в результате чего ток
первичной обмотки увеличивается до
значения
уменьшается входное сопротивление
трансформатора, в результате чего ток
первичной обмотки увеличивается до
значения ![]() ,
при котором оправдывается уравнение:
,
при котором оправдывается уравнение:
![]() вытекающее из условия сохранения
постоянство магнитного потока
трансформатора при переходе от режима
холостого хода к нагрузке. Трансформатор
обладает свойством саморегулирования.
вытекающее из условия сохранения
постоянство магнитного потока
трансформатора при переходе от режима
холостого хода к нагрузке. Трансформатор
обладает свойством саморегулирования.
Справедливость последнего уравнения и вытекающего из него вывода подтверждается экспериментальным изучением работы трансформатора.
Так
как ![]() составляет
составляет ![]() от тока
от тока ![]() ,
то можно при номинальной нагрузке
пренебречь током
,
то можно при номинальной нагрузке
пренебречь током ![]() .
Тогда можно записать
.
Тогда можно записать
![]()
или
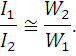
Отсюда следует, что точки в обмотках нагруженного трансформатора обратно пропорциональны числу витков обмоток.
Возвращаясь к ранее приведенному уравнению, можно записать:
![]() называется
приведенным вторичным током, а q=
называется
приведенным вторичным током, а q=![]() коэффициентом приведения.
коэффициентом приведения.
Д ля
нагруженного трансформатора справедливы
так же основные уравнения электрического
состояния.
ля
нагруженного трансформатора справедливы
так же основные уравнения электрического
состояния.
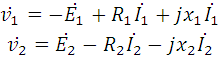
Первое уравнение мы рассмотрели и приводили при анализе холостого хода трансформатора.
Второе
уравнение поясняет то, что напряжение
на вторичной обмотки ![]() при нагрузке не равно, как у ненагруженного
трансформатора, э.д.с.
при нагрузке не равно, как у ненагруженного
трансформатора, э.д.с. ![]() от рабочего потока
от рабочего потока![]() вследствие влияние э.д.с. рассеяния
вызванного потоком
вследствие влияние э.д.с. рассеяния
вызванного потоком ![]() и падения напряжения на сопротивлении
и падения напряжения на сопротивлении
![]() обмотки. Таким образом второе уравнение,
это уравнение по второму закону Кирхгофа
для вторичной цепи.
обмотки. Таким образом второе уравнение,
это уравнение по второму закону Кирхгофа
для вторичной цепи.
Параметры:
![]()
![]()
![]()
![]() соответственно активные и индуктивные
сопротивления рассеяния первичной и
вторичной обмоток трансформатора. На
рисунке 2.4 приведена схема замещения
отдельных обмоток трансформатора.
соответственно активные и индуктивные
сопротивления рассеяния первичной и
вторичной обмоток трансформатора. На
рисунке 2.4 приведена схема замещения
отдельных обмоток трансформатора.

Рисунок 2.4 Схема замещения отдельных обмоток трансформатора
При
расчете электрических цепей с
трансформаторами задача расчета
усложняется из за магнитной связи между
вторичной и первичной обмотками
трансформатора. Эту задачу можно
упростить, если между обмотками составить
эквивалентную электрическую схему без
магнитной связи. Последние возможно
если объединить обе обмотки трансформатора
в одну, сделав равными Э.Д.С. этих обмоток
(![]() (Рис. 2.5).
(Рис. 2.5).
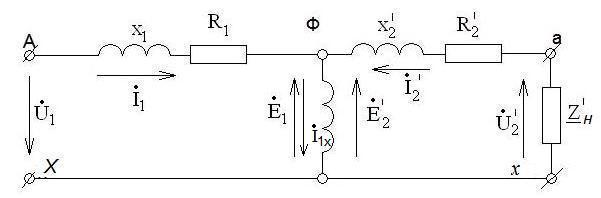
Рисунок
2.5 Схема замещения обмоток трансформатора
при ![]()
Равенство
Э.Д.С. ![]() будет достигнуто, если новое число
витков вторичной обмотки
будет достигнуто, если новое число
витков вторичной обмотки ![]() станет равным
станет равным ![]() .
.
Очевидно,
что при таком преобразовании изменятся
все величины, характеризующие вторичную
цепь ![]() )
и их необходимо пересчитать на новое
число витков. Пересчет величин вторичной
цепи на новое число называется приведением
вторичной цепи к числу витков первичной
цепи, а трансформатор в этом случае
называется приведенным.
)
и их необходимо пересчитать на новое
число витков. Пересчет величин вторичной
цепи на новое число называется приведением
вторичной цепи к числу витков первичной
цепи, а трансформатор в этом случае
называется приведенным.
Упрощенная Т-образная схема замещения приведенного трансформатора (Рис.2.6).
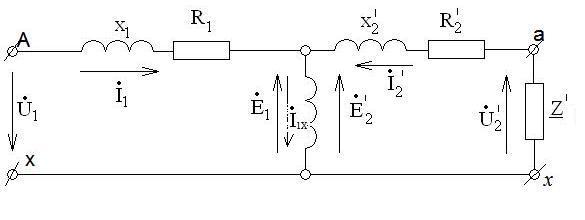
Рисунок 2.6 Т - образная схема замещения приведенного трансформатора
Математически,
возможность замены индуктивной связи
между первичной и вторичной обмотками
трансформатора гальванической связью
достигается умножением левой и правой
частей уравнения электрического
состояния вторичной обмотки на ![]() .
.
![]()
или
![]()
где
![]()
Приведенный нагруженный трансформатор описывается уравнениями электрического состояния и уравнением токов.
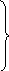
![]()
![]() ,
,
![]()
где
![]()
![]()
![]()
![]()
![]()
Схема замещения приведенного трансформатора (Рис. 2.7).
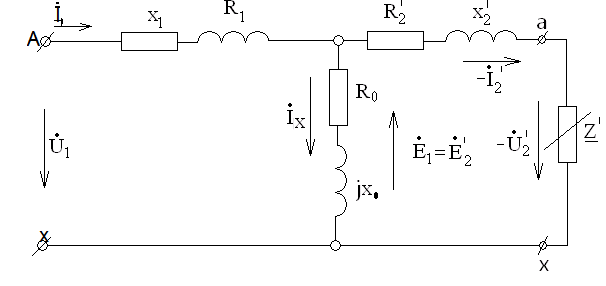
Рисунок 2.7 Схема замещения приведенного трансформатора
Справедливость изображенной схемы вытекает из основных уравнений нагруженного трансформатора.
Действительно, из уравнения электрического состояния
![]()
![]()
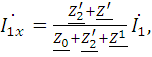 следовательно
следовательно
 =
=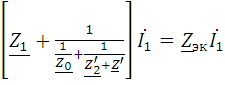
Эквивалентное сопротивление
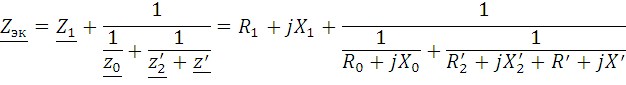
Соответствует комбинации гальванически соединенных на схеме (Рис. 2.7) элементов, которая является схемой замещения приведенного трансформатора.
