1.2 Дифференциальные уравнения второго порядка

Линейные однородные уравнения второго порядка с постоянными коэффициентами.

Общий вид такого уравнения:

где p и q -действительные числа. Корни его характеристического уравнения могут быть:

1. действительными и различными:

2. действительными и равными:

3. комплексными:

Им соответствуют следующие общие решения уравнения:

1. ;

2. ;

3. .

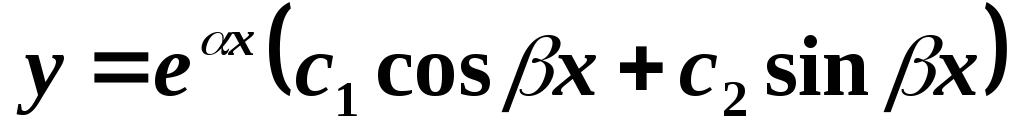Пример 3.

Найти частное решение линейного однородного уравнения второго порядка с постоянными коэффициентами, удовлетворяющее начальным условиям:

Решение:

а) Характеристическое уравнение имеет два различных вещественных корня, поэтому общее решение этого дифференциального уравнения записывается в виде, гдепроизвольные постоянные.

Отсюда

Основываясь на начальных условиях, получаем

Решая систему уравнений 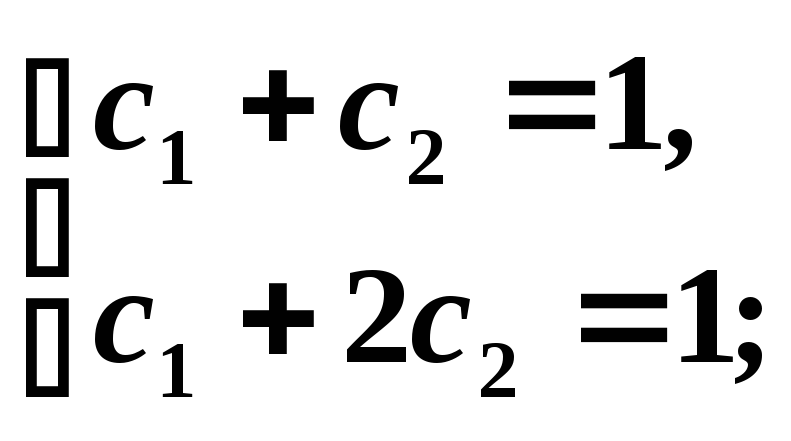получаем=1;=0

Частное решение данного уравнения, удовлетворяющего заданным начальным условиям, приобретает вид

б) Характеристическое уравнение имеет два равных корняпоэтому общее решение соответствующего дифференциального уравнения будет иметь видДифференцируя, получим.

Учитывая начальные условия, получаем систему для определения 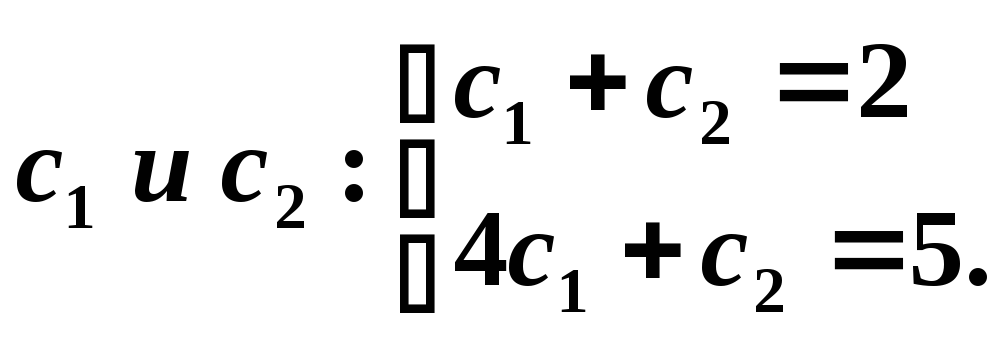Откуда, поэтому частное решение имеет вид:

в) Характеристическое уравнение не имеет действительных корней. Его корни:

Поэтому общее решение данного уравнения имеет вид:

Дифференцируя, получим:

Подставляя в выражения для начальные условия, получим систему уравнений:

решая которую, найдем .

Тогда частное решение данного уравнения будет иметь вид:

Линейные неоднородные уравнения второго порядка с постоянными коэффициентами.

Общий вид такого уравнения: (*)

В правой части: многочлен степени .

Общее решение уравнения (*)может быть представлено в виде

где - общее решение соответствующего линейного однородного уравнения,

- какое- либо частное решение неоднородного уравнения (*).

Для отыскания пользуются следующим правилом:

1. если число не является корнем характеристического уравнения, тогде- многочлен степени с неопределенными коэффициентами;

2. если совпадает с одним из корней характеристического уравнения, то

;

3. если совпадает с обоими корнями характеристического уравнения , то

.

Пример 4

Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами:

Решение:

Будем искать общее решение в виде

Y – общее решение уравнения характеристическое уравнение которогоа его корнии решениеY имеет вид:

Частное решение будем искать в виде

или

Подставим ив исходное уравнение, получим:

или

Составим систему для нахождения А и В.

Тогда частное решение имеет вид: .

Общее решение данного уравнения будет:

.

2. Числовые ряды

Числовым рядом называется выражение

(1)

Ряд называется сходящимся, если сумма n первых его членов имеет предел при . Иначе ряд называется расходящимся. Ряд может сходиться лишь при условии, когда общий член ряда стремится к нулю при :(Это необходимый, но не достаточный признак сходимости для всякого ряда).

Если же , то ряд расходится. (Это достаточный признак расходимости всякого ряда).

Пример 5. Дан ряд . Проверить выполнение необходимого признака.

Необходимый признак не выполняется. Следовательно, ряд расходится.

Пример 6.

Дан гармонический ряд : Найдем для него .

Для него необходимый признак выполняется, вследствие чего он может быть или сходящимся или расходящимся, что можно установить дополнительным исследованием. (Смотри ниже).